哈希——并查集结构——岛问题

一个矩阵中只有0和1两种值， 每个位置都可以和自己的上、 下、 左、 右四个位置相连

如果有一片1连在一起， 这个部分叫做一个岛， 求一个矩阵中有多少个岛？
举例：
0 0 1 0 1 0
1 1 1 0 1 0
1 0 0 1 0 0
0 0 0 0 0 0
这个矩阵中有三个岛

解：

当矩阵数量较少时，解法（使用递归）

两个函数

1.遍历函数：遍历矩阵，遇到为1的点，就调用感染函数

2.感染函数 ：使用递归的方法，将连成一片的1变成2

 

public class Islands {
    //求有多少个岛
    public static int countIslands(int[][] m){
        int row = m.length;
        int col = m[0].length;

        int count = 0;

        for(int i = 0; i < row; i++){
            for(int j = 0; j < col; j++){
                if(m[i][j] == 1){
                    count++;
                    infect(m, row, col, i, j);
                }
            }
        }
        return count;
    }

    //感染函数：通过递归调用，将传入位置(i,j)处以及他的上下左右为1的值都改写成2
    public static void infect(int[][] m, int row, int col, int i, int j){
        if(i >= 0 && i < row && j >= 0 &&j < col && m[i][j] == 1){
            m[i][j] = 2;
            infect(m, row, col, i, j - 1);
            infect(m, row, col, i, j + 1);
            infect(m, row, col, i - 1, j);
            infect(m, row, col, i + 1, j);
        }
    }

    //感染函数：通过递归调用，将传入位置(i,j)处以及他的上下左右为1的值都改写成2
    public static void infect1(int[][] m, int row, int col, int i, int j){
        if(i < 0 || i >= row || j < 0 || j >= col || m[i][j] != 1) return;
        m[i][j] = 2;
        infect1(m, row, col, i, j - 1);
        infect1(m, row, col, i, j + 1);
        infect1(m, row, col, i - 1, j);
        infect1(m, row, col, i + 1, j);
    }

    public static void main(String[] args) {
        int[][] m1 = {  { 0, 0, 0, 0, 0, 0, 0, 0, 0 },
                { 0, 1, 1, 1, 0, 1, 1, 1, 0 },
                { 0, 1, 1, 1, 0, 0, 0, 1, 0 },
                { 0, 1, 1, 0, 0, 0, 0, 0, 0 },
                { 0, 0, 0, 0, 0, 1, 1, 0, 0 },
                { 0, 0, 0, 0, 1, 1, 1, 0, 0 },
                { 0, 0, 0, 0, 0, 0, 0, 0, 0 }, };
        System.out.println(countIslands(m1));

        int[][] m2 = {  { 0, 0, 0, 0, 0, 0, 0, 0, 0 },
                { 0, 1, 1, 1, 1, 1, 1, 1, 0 },
                { 0, 1, 1, 1, 0, 0, 0, 1, 0 },
                { 0, 1, 1, 0, 0, 0, 1, 1, 0 },
                { 0, 0, 0, 0, 0, 1, 1, 0, 0 },
                { 0, 0, 0, 0, 1, 1, 1, 0, 0 },
                { 0, 0, 0, 0, 0, 0, 0, 0, 0 }, };
        System.out.println(countIslands(m2));
    }
}

　　

　　

 

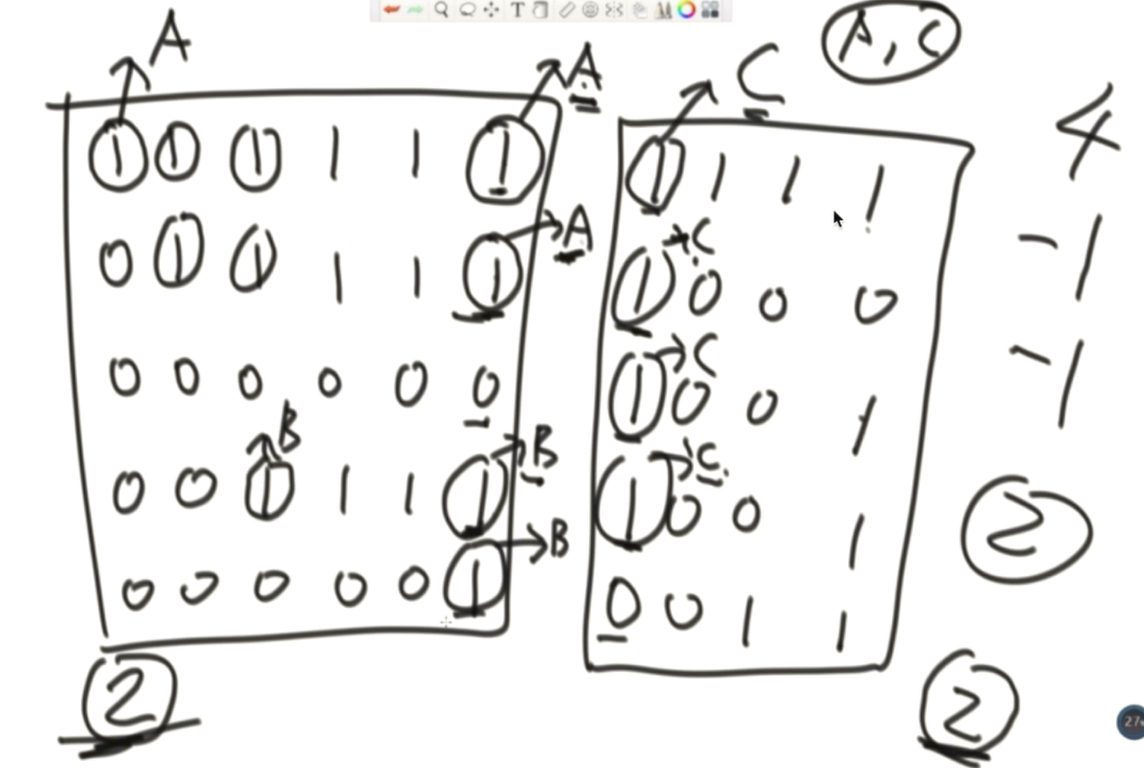
使用并查集时（多任务，并行计算）

将一个大矩阵化成多个小矩阵，然后不同的CPU处理不同的矩阵，最后将不同的矩阵合并，

边界问题，将边界上连成一片的1合并

 在小矩阵中，第一个1作为代表结点，后面1连成一片的1都挂在代表结点下

然后在解决边界时，若两个1碰到一起了，就检查两个1的代表结点是不是一样的，

不一样的话，就合并两个集合，同时岛的个数-1

一样的话，证明之前已经合并过了，岛的个数不变