矩阵--旋转矩阵

给定一个整型正方形矩阵matrix， 请把该矩阵调整成顺时针旋转90度的样子。
【要求】 额外空间复杂度为O(1)。

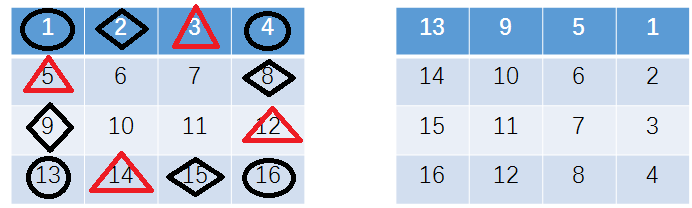
对比上面两图，1,4,16,13是一组，2，8,15,9是一组，3,12,14,5是一组，他们分别和下一个位置上的数交换，

但是实际操作起来，就很难找边界的旋转

通过rotate(int[][] arrays)方法来进行矩阵的旋转，其中的rowStart，rowEnd，colStart和colEnd来控制旋转所进行到的框框，一圈一圈的进行旋转

rotateEdge()方法是控制在旋转这一圈时，所进行的次数，和所对应的四个位置的下标

int tmp = arrays[rowStart][colStart + i];
arrays[rowStart][colStart + i] = arrays[rowEnd - i][colStart];
arrays[rowEnd - i][colStart] = arrays[rowEnd][colEnd - i];
arrays[rowEnd][colEnd - i] = arrays[rowStart + i][colEnd];
arrays[rowStart + i][colEnd] = tmp;

　　

 

完整代码

public class RotateSquare {
    public static void rotate(int[][] arrays){
        int rowStart = 0;
        int rowEnd = arrays.length - 1;
        int colStart = 0;
        int colEnd = arrays[0].length - 1;

        while(rowStart < rowEnd){
            rotateEdge(arrays, rowStart++, rowEnd--, colStart++, colEnd--);
        }
    }

    private static void rotateEdge(int[][] arrays, int rowStart, int rowEnd, int colStart, int colEnd) {
        int times = colEnd - colStart;
        for(int i = 0; i < times; i++){
            int tmp = arrays[rowStart][colStart + i];
            arrays[rowStart][colStart + i] = arrays[rowEnd - i][colStart];
            arrays[rowEnd - i][colStart] = arrays[rowEnd][colEnd - i];
            arrays[rowEnd][colEnd - i] = arrays[rowStart + i][colEnd];
            arrays[rowStart + i][colEnd] = tmp;
        }
    }

    public static void print(int[][] arrays){
        int row = arrays.length;
        int col = arrays[0].length;

        for(int i = 0; i < row; i++){
            for(int j = 0; j < col; j++){
                System.out.print(arrays[i][j] + " ");
            }
            System.out.println();
        }
        System.out.println();
    }

    public static void main(String[] args){
        int [][] arrays = {{1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12}, {13, 14, 15, 16}};
        print( arrays );
        rotate( arrays );
        print(arrays);
    }
}