李宏毅《机器学习》总结 - 如何进行 optimization

核心问题：Critical Point

在 Gradient Descent 的时候，如果遇到梯度为 0 的情况，导致无法继续 optimization，这样的点叫做 Critcal Point
如果最后优化的结果不好，则出现这样的点的原因有 2 个：一个是到 local minima 了，另一个是在驻点了（也叫鞍点，Saddle Point）。现在主要关注的是如何判断是鞍点的情况，并继续 optmization 下去。
有一种数学的方法，是利用黑塞矩阵（类比多元函数的极值求法，写出二元函数的泰勒展开），此处不深究
实践中常用的是减小 batch 和设置一个 momentum，除此之外，还可以自动调整学习率（也就是 $η$ ）

batch

什么是 batch？在梯度下降的时候，需要求出 loss 的梯度，每次求出梯度之后在乘上 learning rate（超参数，即 $η$ ）作为位置的改变量。现在，我将 loss 设置为训练中一部分数据的 loss 值，这一部分数据就叫一个 batch（然后将源数据shuffle之后再分出batch，继续……）
经过研究发现，batch 比较小的时候，优化的效果比较好。（感性理解：可以认为是步长比较小，因此更容易得到最优解，而不是在最优解两头不停震荡）

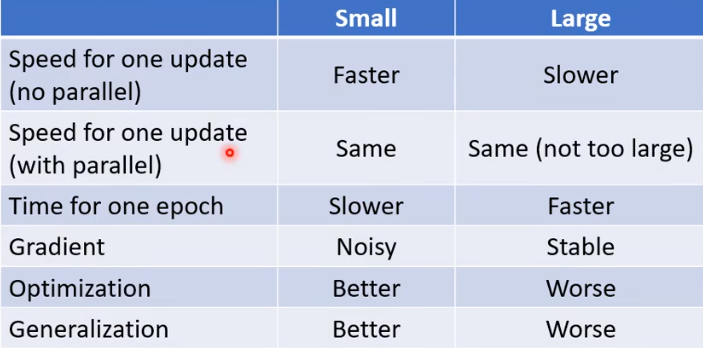
batch size也是一个需要人为决定的超参数。

momentum

考虑在 optimization 的过程中引入“惯性”的概念，每次移动的方向不光是由梯度决定，而是还与之前的移动方向有关。

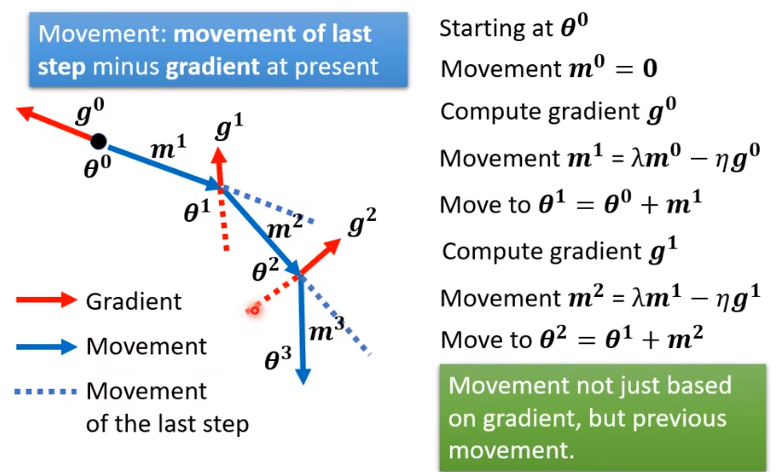
这样，我们就在处理 critical point 的时候不会被梯度为 0 的点卡爆了，因为移动的方向还与之前的移动的方向有关。

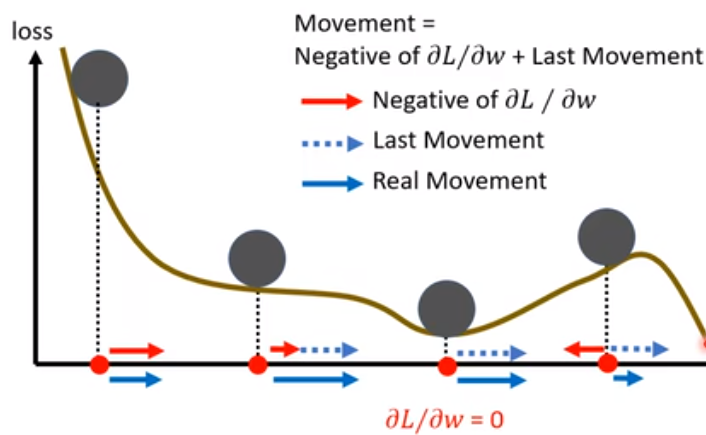
自动调整 learning rate

目前，我们以只有两个参数为例（多个参数的情况完全同理，只不过不容易用图表示），在两个参数为 $(x,y)$ 点处，计算出 loss 值作为这个点的“函数值”，用热力图表示函数值，这样的图叫做 error surface

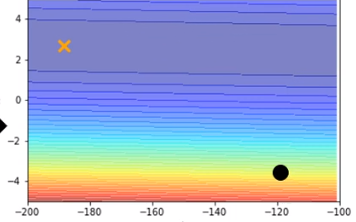
如果 loss 最小的点在一个很“平坦”的空间上，就会导致附近的梯度很小，从而根据 $\theta_i^{t+1} \leftarrow \theta_i^t-\eta g_i^t$ （其中 $\theta_i^t$ 代表我想要 optimize 的参数， $\eta$ 代表 learning rate， $g_i^t$ 代表当前这个位置 loss 函数的梯度）收敛很慢，可能就到达不了这个点。如果把 learning rate 设的大一点呢？那如果最优解在梯度比较大的地方的话，就会导致答案在这附近震荡
能不能根据当前的梯度来设定 learning rate呢？如果梯度大，那就把 learning rate 设的小点，反之同理，使得能够更快的收敛，且不至于震荡。

一个想法（Adagrad）：

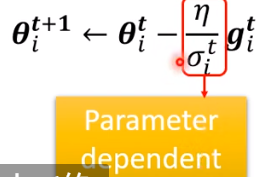
其中， $\sigma_i^t$ 为 $t$ 之前的所有梯度的二次幂平均

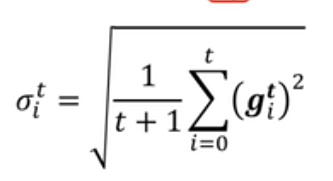
这样，learning rate就是和之前的梯度有关，且成反比，这样也保证了之前所说的要求。
另外一种方法也与之类似，不过略有不同

（RMSProp）：

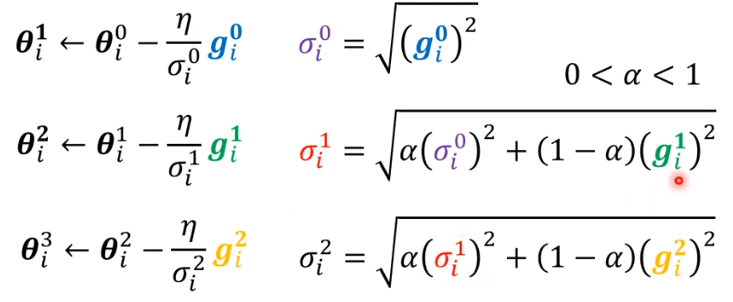
其中 $\alpha$ 也是需要自己决定的超参数，决定了是之前的梯度重要还是当前这次的梯度更重要
这样，当遇到梯度较大的时候，就能“刹住车”了，较小的时候就“踩油门”，解决了这个问题
pytorch 封装好的模型 Adam 就是 RMSProp + Momentum
这样 optimizer 在 error face 跑出来的结果如下：

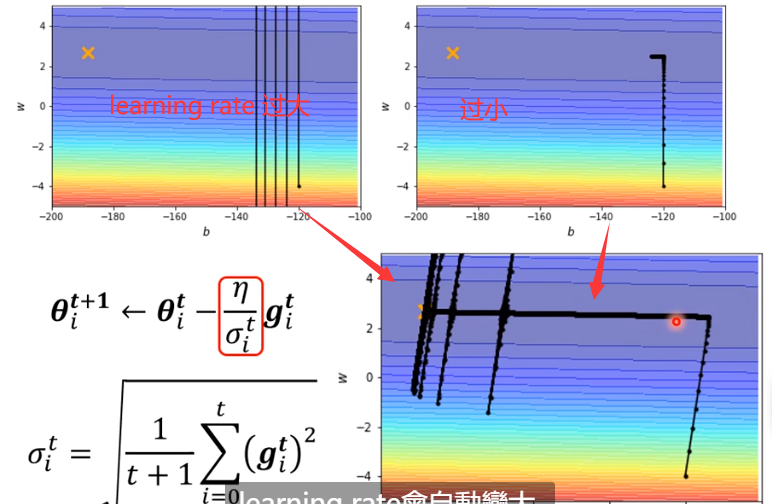
能到最优点了，但是到最后开始震荡了？
因为到最优点附近的梯度很小，就导致 learning rate 很大，就开始震荡了。
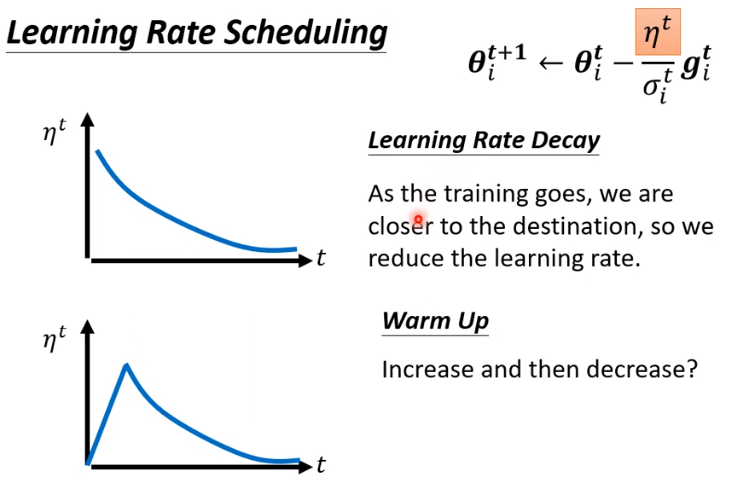
怎么解决这个问题呢？和模拟退火有点类似，将 $η$ 设成是时间的函数，随时间减小。这个过程叫做 learning rate scheduling
$\eta^t$ 有两种写法，都 ok