李宏毅《机器学习》总结 - 回归和分类
回归（Regression）
neural network 工作的核心就是：找函数 - 计算参数对应的 loss - 沿着 gradient 的（逆）方向更新参数使 loss 减小
如何计算 gradient？需要用到 back propogation（反向传播）原理
反向传播
首先，loss 值等于所有输入的数据对应的误差（输出数据与标准数据的误差）之和，因此计算 loss 对某一个参数的梯度只需要计算单组数据的 loss 的梯度即可
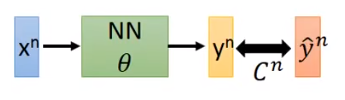
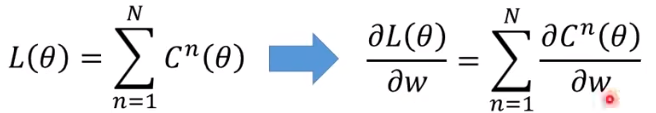
现在的问题转化成计算 （C 对 w 的偏微分）了，考虑链式法则。
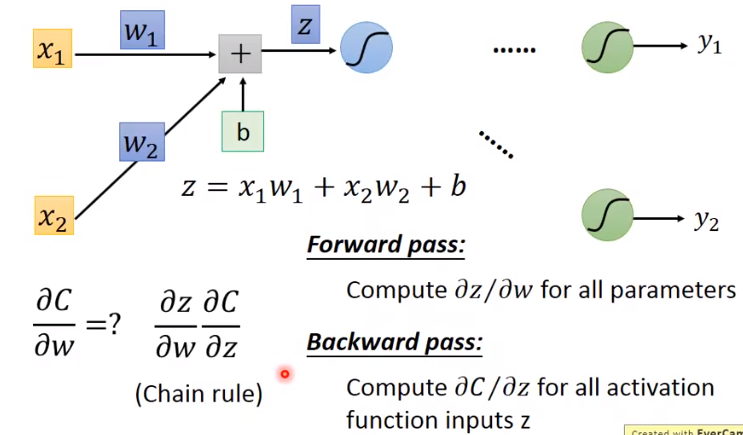
其中，\(\dfrac{\partial z}{\partial w}\) 是容易计算的，等于对应的 x（因为 \(z=x_1w_1+x_2w_2+b\)），这个我们可以正向遍历网络的时候就计算出来，因此叫 forward pass
那如何计算后面的 \(\dfrac{\partial C}{\partial z}\) 呢？这就需要反向传播了。
先试着把 \(\dfrac{\partial C}{\partial z}\) 写出来：
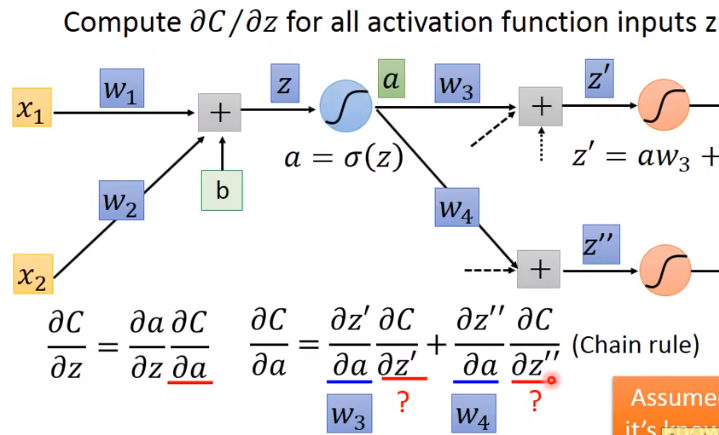
化简得：
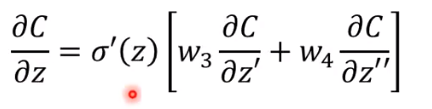
其中 \(\dfrac{\partial a}{\partial z}\) 就是 sigmoid 函数的导数，是已知的
可以发现，如果求 \(\dfrac{\partial C}{\partial z}\) 是依赖于其后面结点的偏导值的。也就是说，如果已知了后面结点的偏导，是可以求出当前点的偏导，进而求出梯度。这启示我们反向。具体的，分当前节点是否为输出层结点：
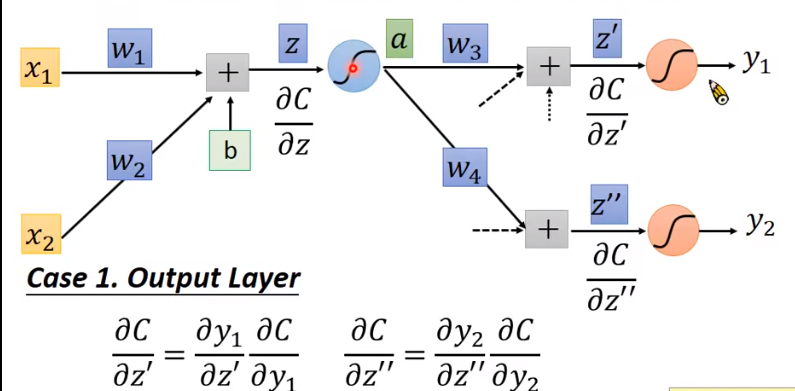
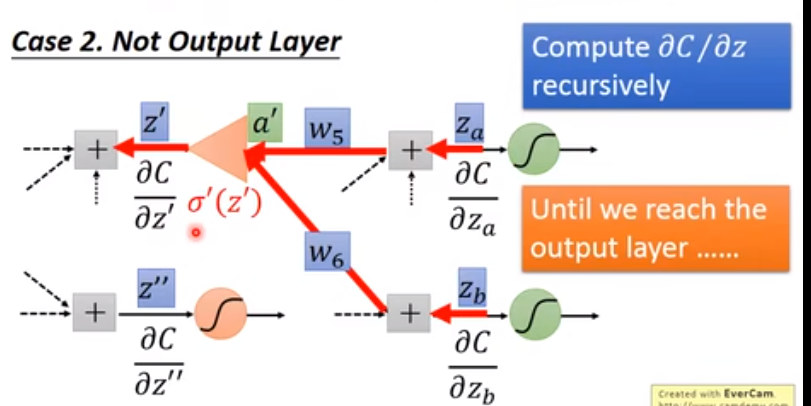
迭代的去做，就可以求了。
分类（Classification）
朴素贝叶斯
朴素贝叶斯（NB）是生成式（Generative）的。通过后验概率来进行分类（如：某一个物品在某一个类别的概率比较大，那么我们就认为这个物品属于这个类别）
不妨假设数据服从二维正态分布，考虑利用训练集确定二维正态分布所需要的参数（均值\(\mu_1, \mu_2\)、协方差\(\Sigma\)）。
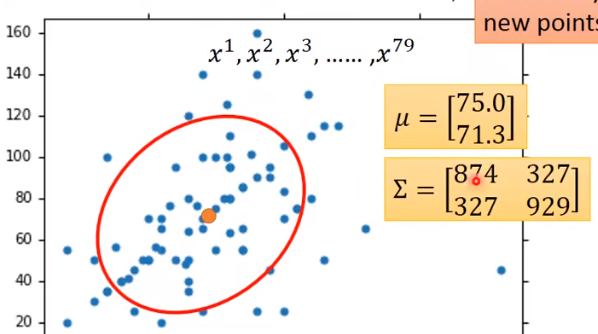
图中的点代表的训练集中某一类别的元素（认为有两个参数），那么可以用考虑用二维正态分布拟合。如何确定二维正态分布的参数？用最大似然估计，即概率密度乘起来，取对数，再求偏导。一个 trick 就是不同类别的元素共用协方差，结果会更优。
逻辑回归（Logistics Regression）
是在贝叶斯公式的基础上继续推导，可以得到 sigmoid 函数。
\(z=wx+b=\sum_iw_i\times x_i+b\)（这里 w 和 x 都是向量，做内积）
定义 \(f_{w,b}(x)=P_{w,b}(C_1|x)=\sigma(z)\)，其中 \(\sigma(z)=\dfrac{1}{1+e^{-z}}\) 代表 sigmoid 函数
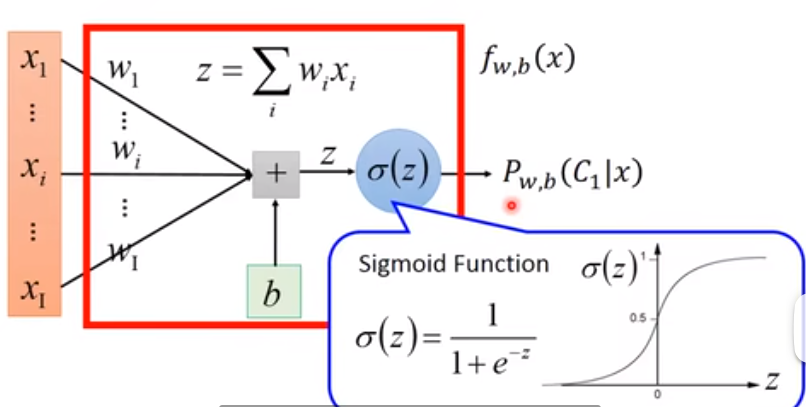
（实际上这和neural network很像了）
然后借助 cross entropy 求出 loss 函数
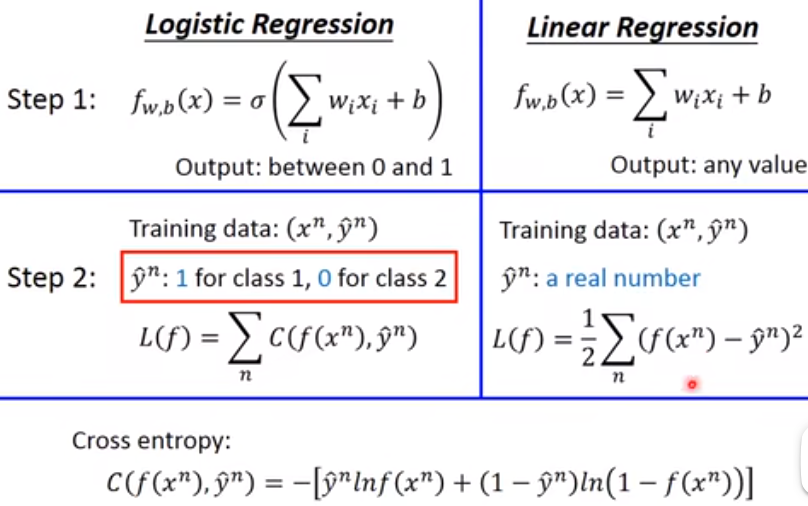
数学推导之后，发现朴素贝叶斯和逻辑回归的更新过程都是这样更新：
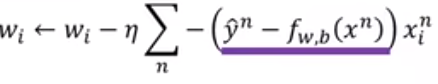
逻辑回归为什么要用 cross entropy 而非残差平方（square error）？因为如果求出这个 loss 关于 w 的偏导数，如果和最优点距离特别近的时候，肯定偏导是比较小的，但是如果距离特别远的时候，偏导也是很小，这样不利于收敛。
另外，逻辑回归进行二分类的时候，实际上是用一条直线将不同类别分隔开的。因此如果两个类别不能用直线分开的话，就会出现问题。
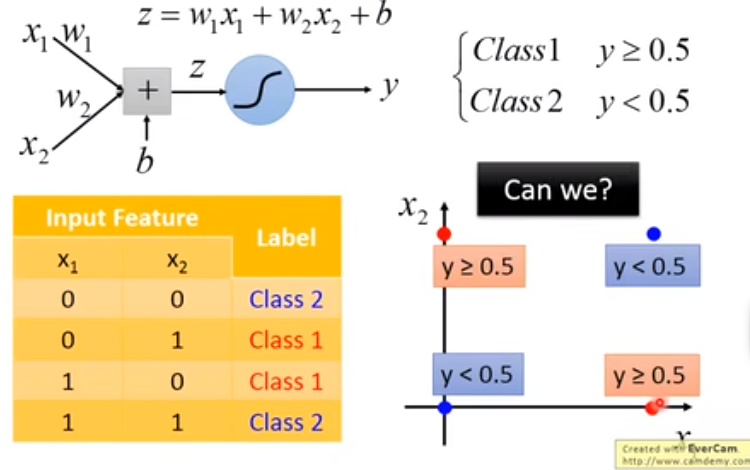
比如这样的两个类就没办法分开。
那么如何处理呢？我们想到，如果将现有的特征做一些变换，新的特征可能就是能用直线分隔开的。如何用机器模拟这个过程？我们想到，可以多重复几次这样的过程。也就是让逻辑回归“更深一点”，这样，如果我们把每个逻辑回归叫做一个 neuron，我们就得到了 DNN 的框架（deep neural network）
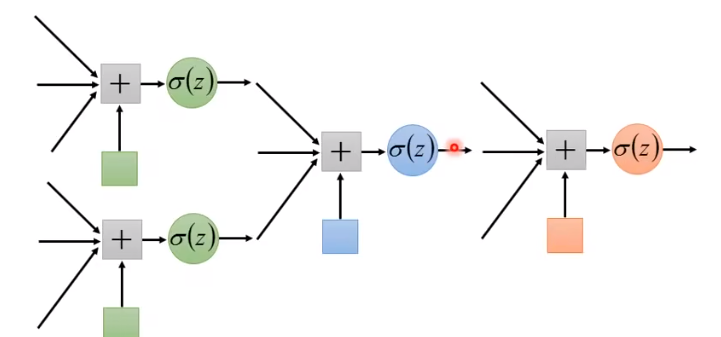
多类别分类（Multi-class classification）
把原来的 sigmoid 函数变成指数之后再标准化，得到一个0~1之间的小数，且和是1，这个过程叫做 softmax
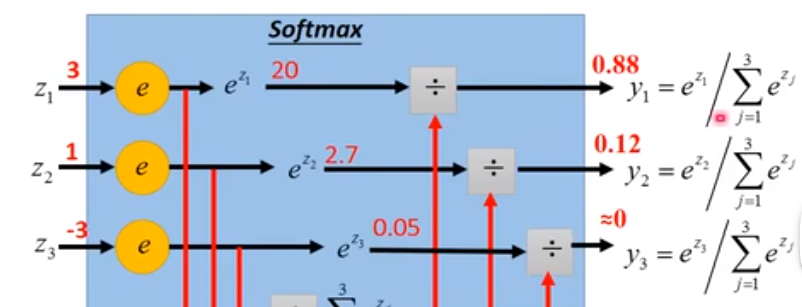
然后得到的 \(y\)，和独热编码（one-hot vector，只有一个地方为 1，其余全为 0），做cross entropy即可得到概率。（图中应为 \(e = -\sum_i \hat y_i \ln y_i\)）
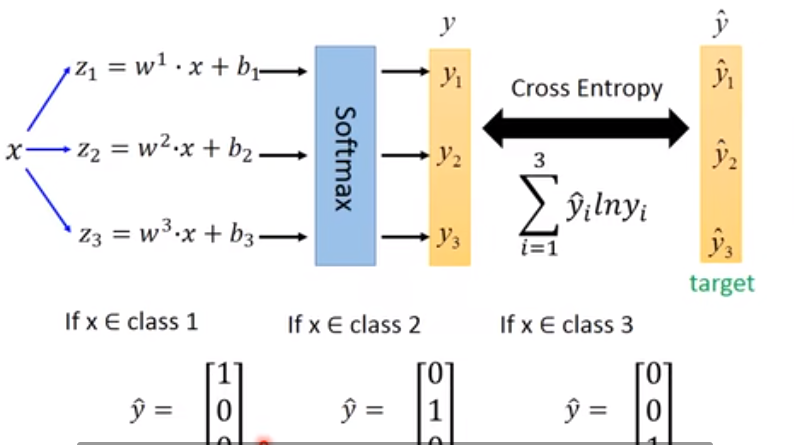
至于为什么用 cross entropy 而不用 MSE（残差平方和），因为在 loss 比较大的时候，cross entropy 更易于 optmization
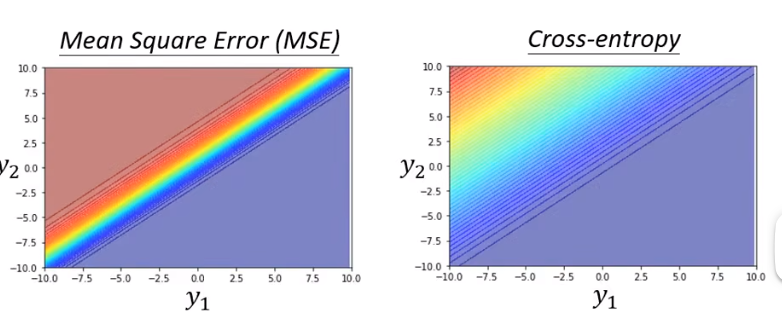
分类总结
实际上还是回归，只不过neural network中回归一般给出的是一个数，在分类问题中得出的是多个数，取 softmax 标准化成 0~1 之间的数且数的和为1。再和不同的one-hot vector做cross entropy（loss）（事实上这也可以看成概率），然后比较哪个得出的值较高，就说明是哪一类。
一种特殊的情况是二分类的 logistic regression，用的方法是拿个 neural network，最后归一化用的是 sigmoid 函数，得出的值直接就是上面流程中的 loss。但是事实上这样的做法和上面再本质上是完全一样的。
