Luogu7509 撕裂消除 - 期望dp -

设 \(f[i][j][0/1]\) 表示考虑到第 \(i\) 个位置，已经形成了极大的 \(j\) 段，当前位置为 0/1 的期望值 ； \(g[i][j][0/1]\) 也同理，不过维护的是概率。

（思考：这种不是求最优决策而是求某种固定的答案的问题，可以再开一个数组维护一下当前状态下的其它值，因为没有决策也就没有 max/min 之类的操作，因此维护比较方便）。

转移方程：

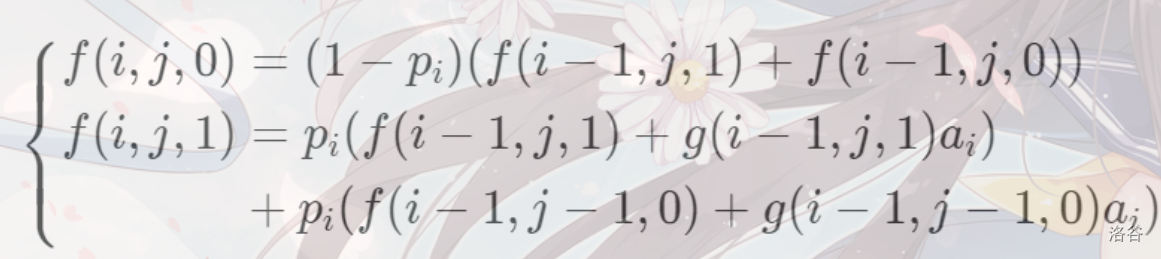
（from 官方题解）

解释：第一个方程就是当前位置取 \(0\) 时的期望，可以由上一位是 0/1 转移过来，概率是 \(1-p_i\)。

第二个方程是当前取 \(1\) 时的。显然也是由 0/1 转移过来，由期望的线性性可以相加。\(f(i-1,j,1)+g(i-1,j,1)a_i\) 代表当前这个状态的期望（再次运用了期望的线性性），因为取 1 也有 \(p_i\) 的概率，所以也要乘一个系数，加号后面的也同理。

注意维护一下 \(j=0\) 的时候的 \(g\) 就行了。

// by SkyRainWind
#include <bits/stdc++.h>
#define mpr make_pair
#define debug() cerr<<"Yoshino\n"
#define rep(i,a,b) for(int (i)=(a);(i)<=(b);(i)++)
#define pii pair<int,int>

using namespace std;

typedef long long ll;
typedef long long LL;

const int inf = 1e9, INF = 0x3f3f3f3f, mod = 998244353, maxn = 2e5+5;

int n,k,a[maxn],p[maxn];
int dp[maxn][22][2], g[maxn][22][2];

ll pw(ll x,int y){
	if(!y)return 1;
	if(y == 1)return x%mod;
	ll mid=pw(x,y>>1);
	if(y&1)return 1ll*mid*mid%mod*x%mod;
	return 1ll*mid*mid%mod;
}

signed main(){
//	freopen("Luogu7509.in","r",stdin);
	scanf("%d%d",&n,&k);
	for(int i=1;i<=n;i++)scanf("%d",&a[i]);
	for(int i=1;i<=n;i++)scanf("%d",&p[i]);
	
	g[0][0][0] = 1;
	for(int i=1;i<=n;i++){
		dp[i][0][0] = 0;
		g[i][0][0] = 1ll * (1-p[i]+mod) * g[i-1][0][0] % mod;
		for(int j=1;j<=min(k, (i+1)/2);j++){
			(dp[i][j][0] += 1ll * (1-p[i]+mod) * (dp[i-1][j][1] + dp[i-1][j][0]) % mod) %= mod;
			(dp[i][j][1] += 1ll * p[i] * (dp[i-1][j-1][0] + 1ll * g[i-1][j-1][0] * a[i] % mod) % mod) %= mod;
			(dp[i][j][1] += 1ll * p[i] * (dp[i-1][j][1] + 1ll * g[i-1][j][1] * a[i] % mod) % mod) %= mod;
			(g[i][j][1] += 1ll * p[i] * (g[i-1][j][1]+g[i-1][j-1][0]) % mod) %= mod;
			(g[i][j][0] += 1ll * (1-p[i]+mod) * (g[i-1][j][1] + g[i-1][j][0]) % mod) %= mod;
		}
	}
	int bs = pw((g[n][k][1] + g[n][k][0])%mod, mod-2);
	cout<<(dp[n][k][1]+dp[n][k][0])%mod;

	return 0;
}