树上点到路径/链的最短距离
结论
树上一个点 \(x\) 到路径 \(u\rightarrow v\) 的最短距离为：
其中，\(dep\) 为该点的深度，\(\operatorname{lca}\) 为两点的最近公共祖先。
证明
我们提取出同时包含 \(x,u,v\) 的最小的子树，下图以红色表示。
我们发现其实只要证明了这样子树的情况结论成立，即可证明所有情况下结论成立，如下图，当子树扩展到整棵树时，子树内节点的 \(dep\) 都会变大相同值（图中示例 \(dep\) 全部 \(+2\)），因此结果并不会变。
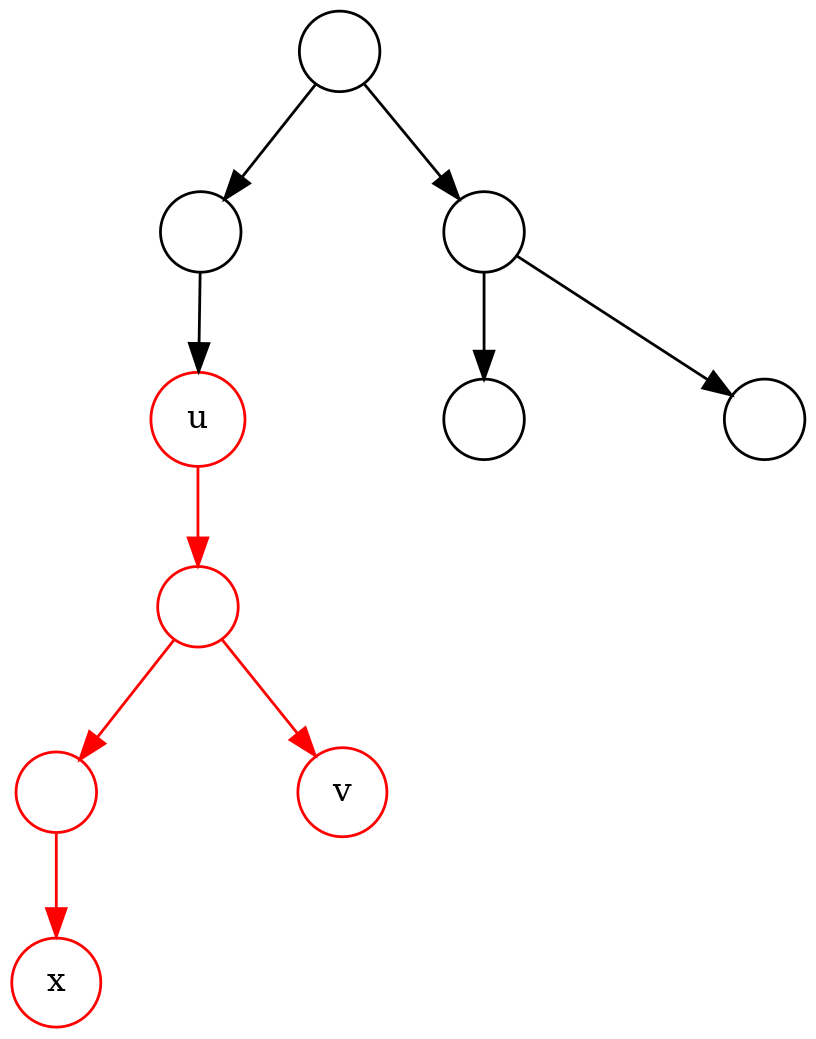
分讨证明
太长不看请跳转分析证明
分讨虽然是一种比较低效的方法，但是看完可能有助于理解，不过看完分讨仍建议继续读分析证明。
情况一 子树根为 \(u,v\) 之一
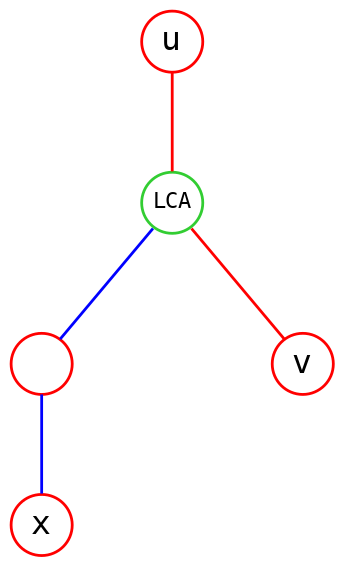
蓝线为最短距离，绿点为路径上离 \(x\) 最近的点。
不妨设此时 \(u\) 为根节点，因为容易发现，结论中的式子 \(u,v\) 交换其实是相等的。
我们发现该情况下 \(x\) 到 \(u\rightarrow v\) 路径上最近的点就是 \(\operatorname{lca}(x,v)\)，距离为 \(dep[x]-dep[\operatorname{lca}(x,v)]\)，而此时 \(dep[\operatorname{lca}(u,v)]\) 与 \(dep[\operatorname{lca}(x,u)]\) 都一定为 \(0\)。该性质对于所有 \(u\) 为根节点的情况都成立，包括下图 \(x\) 为 \(v\) 祖先和 \(v\) 为 \(x\) 祖先的情况。
 |
 |
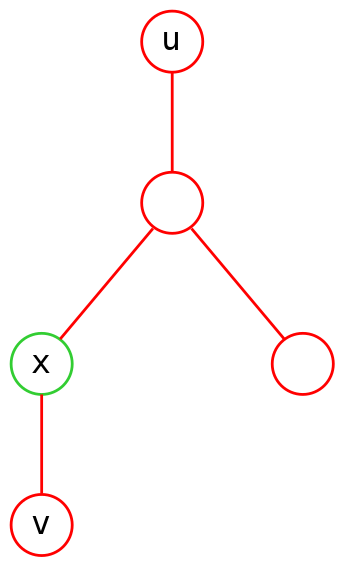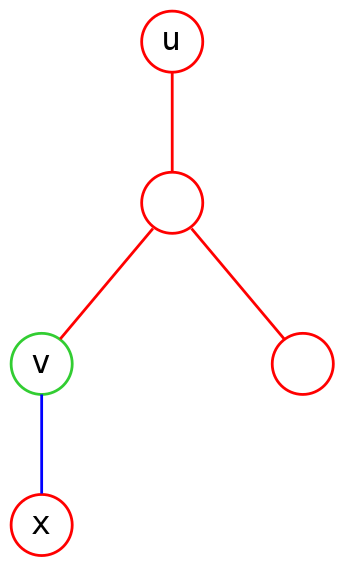情况二 子树根为 \(x\)
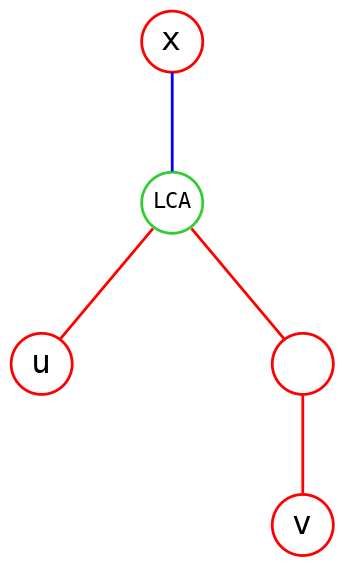
很明显该情况下路径上距离 \(x\) 最近的点为 \(\operatorname{lca}(u,v)\)，因此距离为 \(dep[\operatorname{lca}(u,v)]\)，而由于 \(x\) 是根节点剩下三个 \(dep\) 都为 \(0\)。
情况三 子树根不为 \(x,u,v\) 之一
这是最复杂的一种情况，又分为三种子情况考虑。
这里称（有根）树上两点 \(x,y\) 如果其中一个为另一个的祖先，称它们之间的路径为一条链。
不可能存在 \(u,v,x\) 在一条链上的情况，此时包含它们最小的子树的根一定为 \(u,v,x\) 之一，与情况三条件冲突。
1. \(u,v,x\) 互不成链
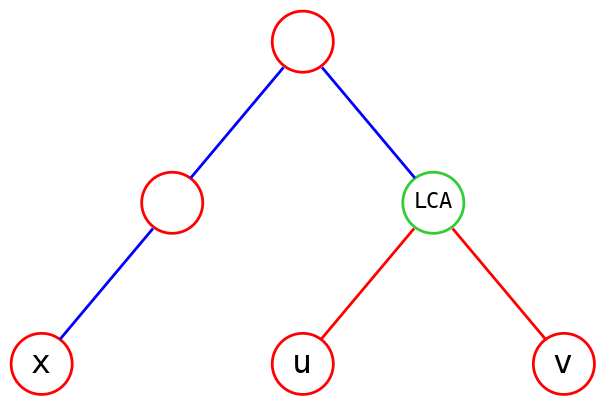
标出 \(dep[x]\) 与 \(dep[\operatorname{lca}(u,v)]\)，加起来正好为答案，此时 \(dep[\operatorname{lca}(x,u)], dep[\operatorname{lca}(x,v)]\) 为 \(0\)。
2. \(u,v\) 成链，但与 \(x\) 不成链
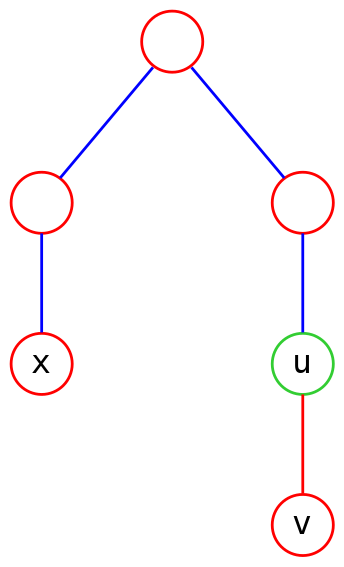
标出 \(dep[x]\) 与 \(dep[\operatorname{lca}(u,v)]\)，加起来为答案，可以发现与 \(x\) 不成链时 \(dep[\operatorname{lca}(x,u)], dep[\operatorname{lca}(x,v)]\) 肯定是为 \(0\) 的。
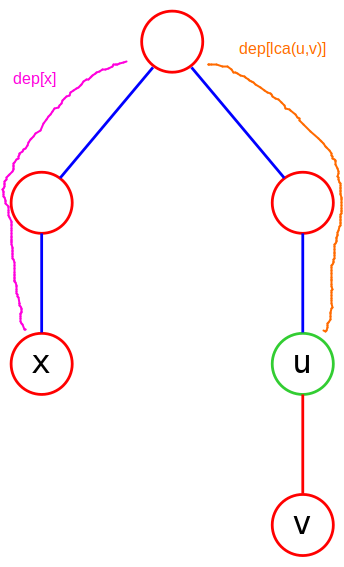
3. \(u,v\) 其中一个与 \(x\) 成链，\(u,v\) 之间不成链
同理此时 \(u,v\) 互换不影响结果，我们不妨设此时与 \(x\) 成链的为 \(u\)。
再分为 \(x\) 为 \(u\) 祖先以及反过来 \(u\) 为 \(x\) 祖先两种情况考虑。
\(x\) 为 \(u\) 祖先
刚好抵消，事实上答案也确实为 \(0\)。
\(u\) 为 \(x\) 祖先
相减为 \(1\)，答案正确。
分析证明
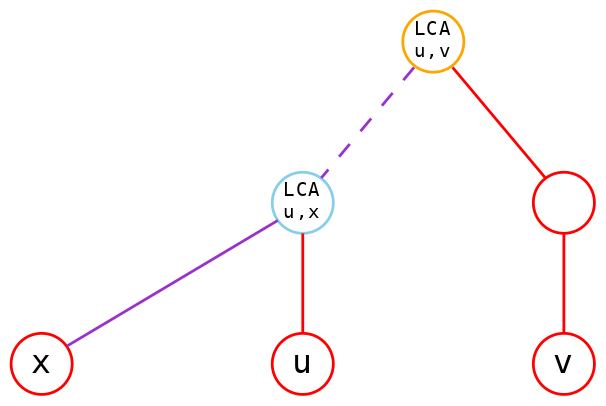
通过上方的枚举，我们可以总结出，其实 \(dep[x]\) 和 \(dep[\operatorname{lca}(u,v)]\) 是在处理 \(x\) 和 \(u,v\) 之间的关系，我们先将 \(u,v\) 当成一个整体用 \(\operatorname{lca}(u,v)\) 来代表，和 \(x\) 算距离，算距离的方式是用两者的 \(dep\) 加起来，最后再用 \(dep[\operatorname{lca}(x,u)]\) 和 \(dep[\operatorname{lca}(x,v)]\) 进行补偿。当然我们可以证明：还需要补偿的情况，一定是 \(\operatorname{lca}(u,v)\) 是子树根节点的情况（如果你想不明白就回去把分讨再看一下吧），因此我们以下的证明均假设 \(\operatorname{lca}(u,v)\) 是子树的根节点。
再进一步说：
\(x\) 在 \(u,v\) 的 LCA 的子树里才需要补偿。
反之 \(x\) 不在 \(u,v\) 的 LCA 的子树里那么 \(dep[x]+dep[\operatorname{lca}(u,v)]\) 已经足够，不需要补偿。
只是为了得到一个通式把两种情况合并成了一个式子。
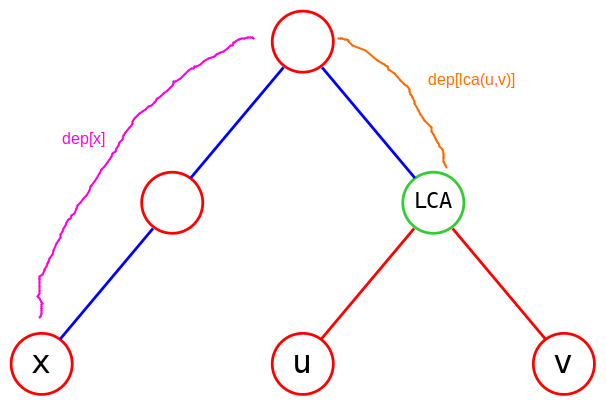
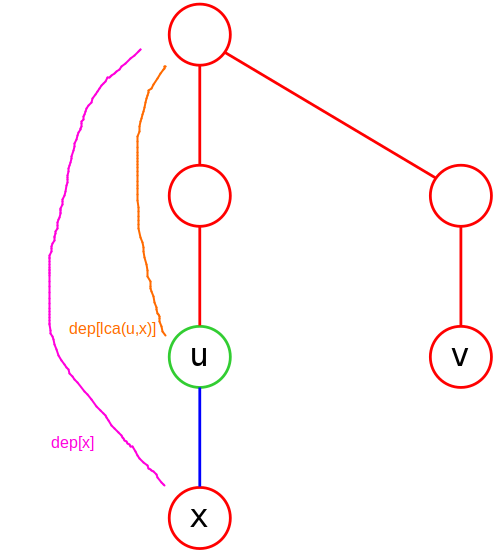
具体怎么补偿呢？看下图，我们先把 \(dep[x]\) 和 \(dep[\operatorname{lca}(u,v)]\) 加起来，也就是所有的紫色部分，我们原先以为 \(x\) 到 \(u\rightarrow v\) 路径上最近的点是 \(\operatorname{lca}(u,v)\)，但我们发现事实上不是，\(x\) 到 \(\operatorname{lca}(u,v)\) 的路径和 \(u\) 到 \(v\) 的路径有一部分重合了啊，于是把重合的虚线部分减掉。那这个虚线部分到底是怎么算出来的呢？我们知道树上每个点到根节点的路径是唯一的，我们也知道树上两个点的路径是从一个点出发到 LCA 再到另一个点，因此重合的部分当然就是 \(x\) 到 \(\operatorname{lca}(u,v)\) 的路径和 \(u\) 到 \(\operatorname{lca}(u,v)\) 的路径第一个重合的点（即 \(\operatorname{lca}(x,u)\)）到 \(\operatorname{lca}(u,v)\) 的部分，这部分距离就是 \(dep[\operatorname{lca}(x,u)]\)。
你说那现在 \(dep[\operatorname{lca}(x,u)]\) 的事解决了，那还要减 \(dep[\operatorname{lca}(x,v)]\) 干啥呢？你有没有发现这时候 \(dep[\operatorname{lca}(x,v)]=0\)？可以证明相同情况下 \(dep[\operatorname{lca}(x,u)]\) 和 \(dep[\operatorname{lca}(x,v)]\) 最多只会有一个起到补偿，一个有值另外一个一定为 \(0\)，不存在两者同时不为 \(0\) 的情况，只是我们为了得到一个通式于是两个都减了。
