NOI模拟 序列

涉及知识点：分治、贪心

前言

没错……又是一道叫序列的题……

题意

有一个长为 \(n\ (\leq10^5)\) 的序列 \(a\)，你可以花费 \(x^2\) 的代价将 \(a_i\) 变成 \(a_i+x\)，使得“代价”加上“\(a\) 两两数之差的绝对值乘以一个给定常数 \(c\)”的总和最小。

思路

拿到手觉得是一个贪心，但是直接贪有很多阻碍，一个数变大需要考虑很多因素。但我们发现，从最小的那个数入手相对来说更简单一些，最小的数变大，直到赶上第二小的数之前，代价的两个影响因素都是单调变化的——差值越来越小、\(x^2\) 越来越大。

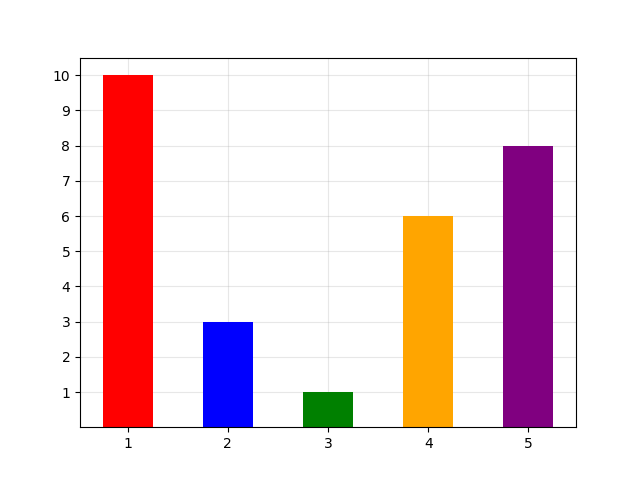
假设 \(a_3\) 一直变大更优，直到 \(a_2=a_3\)。

那这时，\(a_3\) 继续变大还会优吗？

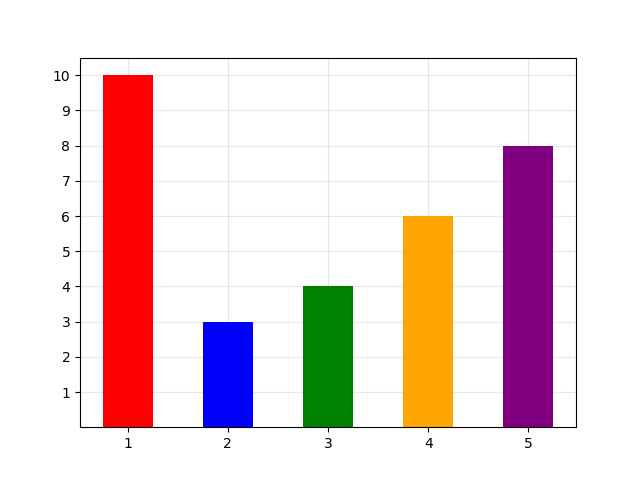
很明显，\(a_3\) 再变大不优了，虽然 \(a_4-a_3\) 的差值变小了 \(1\)，但是 \(a_3-a_2\) 的差值也变大了 \(1\)，二者抵消，但是我们还会多付出 \(a_3\) 变大的 \(x^2\) 的代价。因此我们总结出：当自己增加到和左右相邻的某个数一样大的时候，那么两个数之后只会要么一起增加要么一起停止才优。

形象地说，我们要将最底下的数往上推，推到旁边有一样高的就带着它一起推，直到推不动为止。

但是事情没这么简单，当遇到下面这种例子时，就不能简单的从最小的数向上一次推完。

我们可以用分治：每次找到区间内最大的数记为 \(a_{maxid}\)，以它为基准将区间划为左右部分，递归左右部分查询它们是否能够到 \(a_{maxid}\)​ 的高度，如果两边都可以的话就可以将当前这个大区间视为一个整体往上推，否则不优。

可以证明此时大区间左右相邻的数一定都大于等于区间内所有数，不会出现大区间推的比旁边还高的情况。

而如何查询能否到某个高度呢？我们发现向上推 \(h\) 层与推 \(h+1\) 层的区别在于，差值的贡献会减小 \(2c\) 或者 \(c\)（如果是 \(a_1\) 或 \(a_n\)），而每个数的代价会增多 \((x+1)^2-x^2=2x+1\)，因为此时差值和代价是满足单调性的，所以其实我们只用找代价增大值大于差值减小值的第一个 \(h\rightarrow h+1\) 即可，这个分界点可以二分求出，意味着这个整体能继续向上最多推 \(h\) 层。

实现

以上叙述了大体思路，下面具体讲述分治和二分的具体实现。

变量名意义：

n,c,a: 同题面
l,r,len: 分治的区间及区间长度
aimh: 区间整体希望达到的高度
maxid: 同上文，区间内最大的数的下标
resl,resr: 左右子区间分治的返回值，为一个pair，first为子区间内增加的高度总和（见下文），second为子区间最大能达到的高度
totadd: 当前区间增加的高度总和（见下文）
pos: 当前区间是否左右两边都相邻有数
L,R,mid,res: 二分用变量
ans: 总答案，初始值为不经过任何修改的差值总和，每次修改后将减小的差值加上去得到最终答案。

1. 首先判断一下是不是已经分治完了。

   if(l>r) return mkp(0,-1);
   

2. 获取左右子区间的返回值，如果无法到达 a[maxid]，那么整个区间就没法一起向上推了。

   int maxid=getmaxid(l,r);
   pii resl=solve(l,maxid-1,a[maxid]),resr=solve(maxid+1,r,a[maxid]);
   if((resl.second!=-1 && resl.second!=a[maxid]) || (resr.second!=-1 && resr.second!=a[maxid])) return mkp(0,0);
   

3. 二分找到第一个代价增大值大于差值减小值的增加高度（是增加的高度不是总高度！）。

   LL totadd=resl.first+resr.first,pos=(l==1||r==n)?1:2;
   int L=0,R=MAXA,mid,res=0,len=r-l+1;
   while(L<=R){
       mid=(L+R)/2;
       if(2*(totadd+mid*len)+len > pos*c){
           res=mid;
           R=mid-1;
       }
       else L=mid+1;
   }
   

   • 如何理解 2*(totadd+mid*len)+len 为代价增大值？

     我们要清楚所谓 \((x+1)^2-x^2=2x+1\) 中的 \(x\) 是该点已经增加过的高度值而非该点的高度，假设某个点 \(a_i\) 已经增加过 \(\Delta h_i\)，那么它高度再增加 \(1\) 的代价为 \(2\Delta h_i+1\)。所以我们记录下该区间内所有点已经增加过的高度值记为 \(totadd\)，另外由于在二分中我们计算的是 \(mid\rightarrow mid+1\) 这轮的代价，所以区间内每个点还得“假设”增高了 \(mid\)，因此计算时我们直接用乘法分配率整合了区间内所有点已经增加过的高度 \(x=totadd+mid*len\)。后面加的 \(len\) 很好理解，一个点增高最后要 \(+1\)，那 \(len\) 个点增高总共就是加 \(len\)。

   • 如何理解 pos*c 为差值减小值？

     如果它在边上（\(a_1\) 或 \(a_n\)），那么它变化只会影响和一个数的差值，否则为两个。

4. 二分结束后，如果无论 \(mid\)​ 怎么取都不优，那么干脆就不增加了，返回。

   if(L<1) return mkp(totadd,a[maxid]);
   

5. 如果可以增加很多甚至超过了希望达到的高度（区间相邻的点的高度），那没必要，只需要增加到一样高即可。

   res=min(res,aimh-a[maxid]);
   

6. 统计对答案的贡献。

   ans+=((2*totadd+len)+(2*(totadd+(res-1LL)*len)+len))*res/2 - pos*res*c;
   

   • 如何理解 ((2*totadd+len)+(2*(totadd+(res-1LL)*len)+len))*res/2？

     这是一个等差数列求和，2*totadd+len 为起点，即该区间作为整体向上推一次时的贡献；2*(totadd+(res-1LL)*len)+len) 为终点，即该区间作为整体向上推第 \(res-1\) 次的贡献。至于这东西为什么是等差数列是容易证明的。

   • 如何理解 pos*res*c？

     很明显，这是这个区间作为整体与它相邻点差值的减小值。

7. 返回。

   return mkp(totadd+1LL*res*len,a[maxid]+res);
   

代码

#include<bits/stdc++.h>
#define mkp make_pair
using namespace std;
#ifdef ONLINE_JUDGE
#define getchar __getchar
inline char __getchar(){
    static char ch[1<<20],*l,*r;
    return (l==r&&(r=(l=ch)+fread(ch,1,1<<20,stdin),l==r))?EOF:*l++;
}
#endif
template<class T>inline void rd(T &x){
    T res=0,f=1;
    char ch=getchar();
    while(ch<'0' || ch>'9'){if(ch=='-')f=-1; ch=getchar();}
    while('0'<=ch && ch<='9'){res=res*10+ch-'0';ch=getchar();}
    x=res*f;
}
template<class T>inline void wt(T x,char endch='\0'){
    static char wtbuff[20];
    static int wtptr;
    if(x==0){
        putchar('0');
    }
    else{
        if(x<0){x=-x;putchar('-');}
        wtptr=0;
        while(x){wtbuff[wtptr++]=x%10+'0';x/=10;}
        while(wtptr--) putchar(wtbuff[wtptr]);
    }
    if(endch!='\0') putchar(endch);
}
typedef long long LL;
typedef pair<int,int> pii;
const int MAXN=1e5+5,MAXA=1e6+5,MAXB=18;
int n,c,a[MAXN],lg[MAXN];
LL ans=0;
pii st[MAXN][MAXB];
inline pii getmax(const int& l,const int& r){
    int lglen=lg[r-l+1];
    return max(st[l][lglen],st[r-(1<<lglen)+1][lglen]);
}
pii solve(int l,int r,int aimh){
    if(l>r) return mkp(0,-1);
    int len=r-l+1,maxid=getmax(l,r).second;
    pii resl=solve(l,maxid-1,a[maxid]),resr=solve(maxid+1,r,a[maxid]);
    if((resl.second!=-1 && resl.second!=a[maxid]) || (resr.second!=-1 && resr.second!=a[maxid])) return mkp(0,0);
    LL totadd=resl.first+resr.first,pos=(l==1||r==n)?1:2;
    int L=0,R=MAXA,mid,res=0;
    while(L<=R){
        mid=(L+R)/2;
        if(2*(totadd+mid*len)+len > pos*c){
            res=mid;
            R=mid-1;
        }
        else L=mid+1;
    }
    if(L<1) return mkp(totadd,a[maxid]);
    res=min(res,aimh-a[maxid]);
    ans+=((2*totadd+len)+(2*(totadd+(res-1LL)*len)+len))*res/2 - pos*res*c;
    return mkp(totadd+1LL*res*len,a[maxid]+res);
}
int main(){
    // freopen("seq.in","r",stdin);
    // freopen("seq.out","w",stdout);
    rd(n);rd(c);
    lg[1]=0;
    for(int i=2;i<=n;i++) lg[i]=lg[i/2]+1;
    for(int i=1;i<=n;i++){
        rd(a[i]);
        st[i][0]=mkp(a[i],i);
        if(i>1) ans+=1LL*c*abs(a[i]-a[i-1]);
    }
    for(int j=1;j<MAXB;j++){
        for(int i=1;i+(1<<j)-1<=n;i++){
            st[i][j]=max(st[i][j-1],st[i+(1<<(j-1))][j-1]);
        }
    }
    solve(1,n,getmax(1,n).first);
    wt(ans);
    return 0;
}