省选模拟 序列

题面

Link

给定一个长度为 \(n\) 的序列 \(a\)，可以进行无限次下列操作：

对于 \(i\in [2,n-1]\)，依次执行（而不是择一执行）

\[a[i-1]+=a[i] \\ a[i+1]+=a[i] \\ a[i]=-a[i] \]

求最小的 \(\max^n_{i=1} |a[i]|\)

思路

考虑一次操作对于序列前缀和的影响，对于 \(x,y,z\)，其前缀和为 \(x,x+y,x+y+z\)，一次操作后原序列变为 \(x+y,-y,z+y\)，其前缀和变为 \(x+y,x,x+y+z\)，相当于对于任意连续的三个元素做一次操作，等价于前两个元素前缀和互换。而我们又知道，对于一个数列，相邻元素交换，最终可以构成任何这些元素的排列。因此题目转化为：重新排列前缀和数组 \(pre\) 的 \([1,n-1]\) 区间（由上述推论可知 \(pre[n]\) 永远不会被交换），使得 \(pre\) 两两元素之差尽可能小（包括 \(pre[1]\) 与 \(0\) 之差和 \(pre[n-1]\) 与 \(pre[n]\) 之差）。

可以构造出最优排列方案：

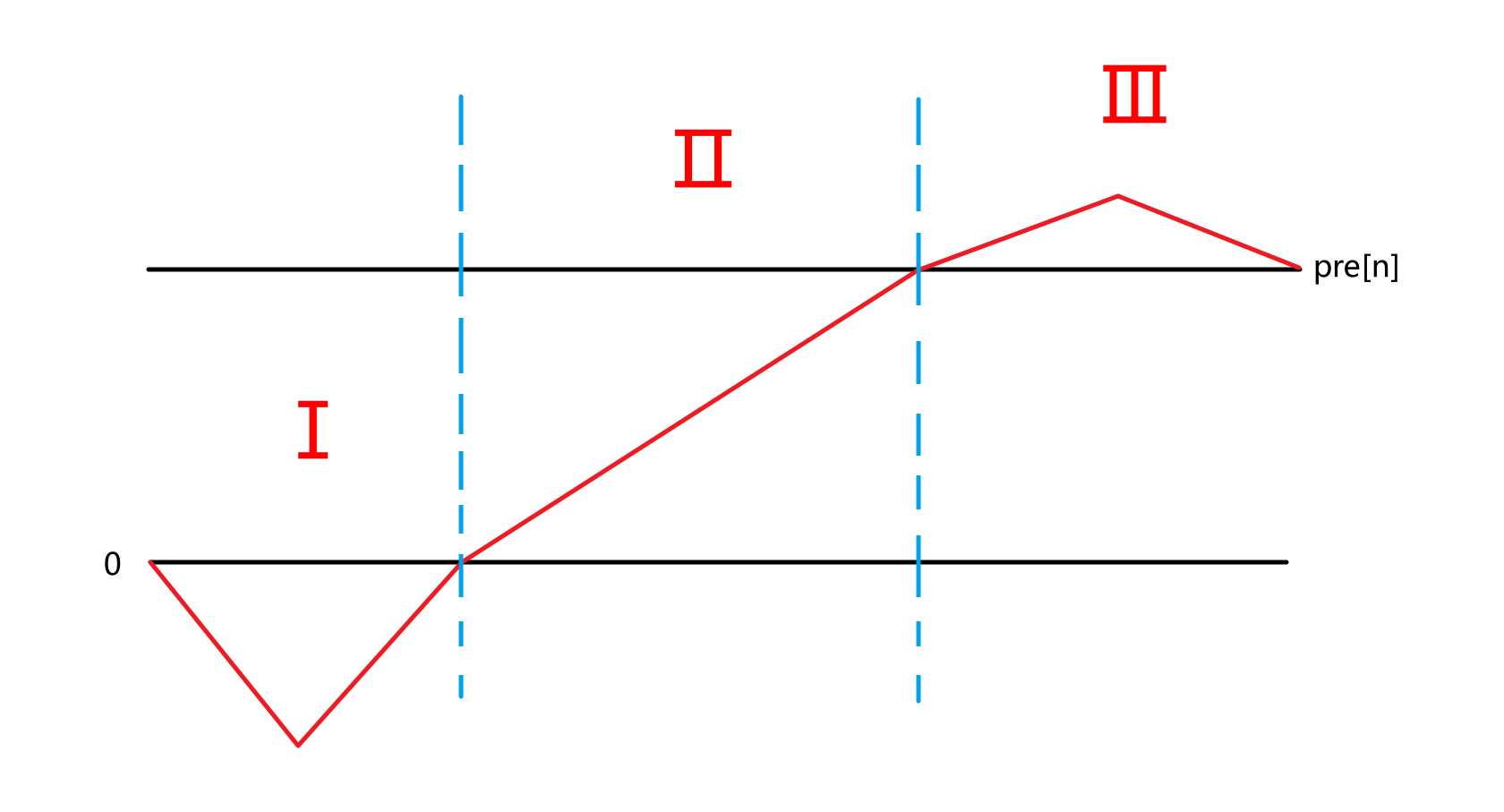
• 第Ⅰ段：取所有小于 \(0\) 的 \(pre[i]\)，逐渐递减再递增，具体实现即为从大到小依次左边放一个右边放一个直至放完（参见注意事项）

• 第Ⅱ段：取所有大于等于 \(0\) 小于 \(pre[n]\) 的 \(pre[i]\)，直接从小到大排列

• 第Ⅲ段：取所有剩下的大于 \(pre[n]\) 的 \(pre[i]\)，逐渐递增再递减，具体实现即为从小到大依次右边放一个左边放一个直至放完

参见示意图：

具体证明：

对于Ⅱ段，显然顺序排列最优
对于Ⅰ、Ⅲ段：

• 若交换对象在同一递增/递减区间，交换后打破了单调性，差值只会变高，不优
• 若交换对象在不同单调性区间，交换后即使未打破单调性，也造成一边差值更小一边差值更大的不平衡情况，不优

注意事项

1. 需要注意判断Ⅰ段与Ⅲ段长度的奇偶，处理落单的数

2. 第Ⅰ段开头需要与 \(0\) 做差而结尾需要与后面大于 \(0\) 的数做差，为使答案最优，应该从大到小从左边开始左右依次放，反之第Ⅲ段需要从小到大从右边开始

3. \(pre[n]\) 为负时，为了方便处理，需要将 \(pre\) 全部取反，由于答案是绝对值，因此不影响答案

代码

#include<bits/stdc++.h>
using namespace std;
template<class T>inline void rd(T &x){
    T res=0,f=1;
    char ch=getchar();
    while(!isdigit(ch)){if(ch=='-')f=-1; ch=getchar();}
    while(isdigit(ch)){res=res*10+ch-'0';ch=getchar();}
    x=res*f;
}
template<class T>inline void wt(T x){
    if(x<0){x=-x;putchar('-');}
    if(x>9) wt(x/10);
    putchar(x%10+'0');
}
const int MAXN=3e5+5;
typedef long long LL;
int n,a[MAXN];
LL pre[MAXN],ans[MAXN];
vector<LL>v1,v2,v3;
int main(){
    int t;
    rd(t);
    while(t--){
        pre[0]=0;ans[0]=0;
        v1.clear();v2.clear();v3.clear();
        rd(n);
        for(int i=1;i<=n;i++){
            rd(a[i]);
            pre[i]=pre[i-1]+a[i];
        }
        if(pre[n]<0){
            for(int i=1;i<=n;i++){
                pre[i]=-pre[i];
            }
        }
        for(int i=1;i<n;i++){
            if(pre[i]<0) v1.push_back(pre[i]);
            else if(pre[i]<pre[n]) v2.push_back(pre[i]);
            else v3.push_back(pre[i]);
        }
        sort(v1.begin(),v1.end(),greater<LL>());
        sort(v2.begin(),v2.end());
        sort(v3.begin(),v3.end());

        int l=1,r=v1.size();
        for(int i=0;i<v1.size() && l<r;){
            ans[r]=v1[i];r--,i++;
            ans[l]=v1[i];l++,i++;
        }
        if(l==r){//v1长度为奇数
            ans[l]=v1[v1.size()-1];
        }

        for(int i=0;i<v2.size();i++){
            ans[v1.size()+1+i]=v2[i];
        }

        l=1,r=v3.size();
        for(int i=0;i<v3.size() && l<r;){
            ans[v1.size()+v2.size()+l]=v3[i];l++,i++;
            ans[v1.size()+v2.size()+r]=v3[i];r--,i++;
        }
        if(l==r){//v3长度为奇数
            ans[v1.size()+v2.size()+l]=v3[v3.size()-1];
        }

        ans[n]=pre[n];
        LL maxx=-1e10;
        for(int i=1;i<=n;i++){
            maxx=max(maxx,abs(ans[i]-ans[i-1]));
        }
        wt(maxx);
        putchar('\n');
    }
    return 0;
}

启示

遇到对序列比较复杂、涉及多个元素的操作时，可以尝试研究操作对于序列前缀和、差分等的影响，将操作的影响简化，由此找到更优异的性质。