AGC027E ABBreviate
涉及知识点:DP、Ad-hoc
Update:大改,原先的解释有巨大 bug。
前言
可能是最简单的解法了。
这种做法太巧妙了,也启发了我们一些其他的类似二元字符串的问题。
题面
给你一个 \(n\) 个字符的字符串 \(s\),该字符串只由小写字母 \(a\) 和 \(b\) 组成,你能进行如下两种操作:
- 将子串
aa替换为b。 - 将子串
bb替换为a。
请问在进行若干次这样的操作后,最后可以得到多少种本质不同的字符串(对 \(10^9+7\) 取模)?
思路
我们首先直接特判没有任何相邻相同字符的情况。且容易证明,只要原串存在至少一对相邻相同字符,该串最后一定可以转化为一个字母。
我们把 a 用 \(1\) 表示,b 用 \(2\) 表示,我们惊喜的发现,对于题中描述的操作,操作前后字符串的字符和在 \(\bmod 3\) 意义下是相等的。
同时我们也可以发现,若干操作后生成的字符串的每个字符一定能对应原串的一段区间,并且结合刚才我们新定义的表示法,原串区间的字符和在模 \(3\) 意义下与最终的字符相等。即对于原串的任意合法区间(“合法”指存在相邻相同字符),如果区间和模 \(3\) 意义下等于 \(1\),则该区间最后可以通过一系列操作最后变为字符 a;等于 \(2\) 最后会变为字符 b;等于 \(0\) 则说明这段区间无法缩成一个字符。
于是我们的任务便转化为:在原串上分段,然后把每段转化成一个字符,问求能得到多少种本质不同的字符串。
(重点)并且我们还能发现,我们实际上并不需要在划分的时候保证每个划分段内有相邻相同字符,因为不合法(上文定义)的划分可以转化为合法的划分!这一点在很多题解里都没有提到,但却是本解法正确性的关键保证!
注意:不合法仅指区间内不存在相邻相同字符,但是区间和模 \(3\) 仍不能为 \(0\),不然无法缩成一个字符!
证明:
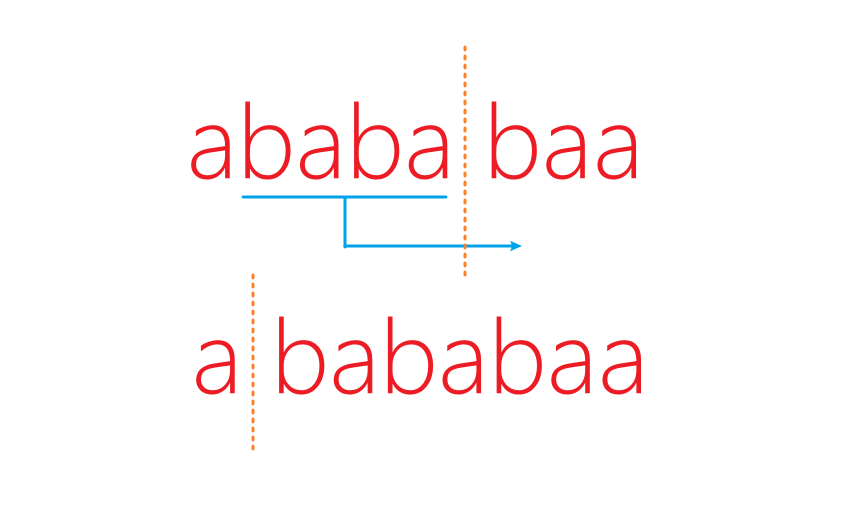
我们考虑这个串 abababaa,有一种不合法的划分,比如 a|bab|aba|a,合并后为 abaa,那么这个不合法的划分如何转化成合法的呢?将划分方式改为 a|b|a|babaaa,合并后还是 abaa。
欸?是巧合吗?并不是!我们可以发现,不合法的区间一定是形如 ababa...aba 或者 babab...bab 的形式(不存在 abab...ab 或者 baba...ba,因为这样区间和就为 \(0\) 了),以 ababa...aba 为例,一定可以拆成 a|baba...aba 或者 aba...abab|a,也就是左边或者右边单独拆出个 a,然后把另一边和原区间左边或右边的区间合并,因为另一半模 \(3\) 下的和为 \(0\),所以模 \(3\) 意义下的区间和仍不变,但划分变合法了。
有人会说这是因为右边这个区间 baa 是合法的,要是左右的区间都不合法怎么办?
运气好的话,接上旁边刚好就合法了:

运气不好的话,我们可以像击鼓传花一样,把这一大段 ababab...ababab 传到直到一个合法段。

因此得到结论:如果能通过不合法的划分方案得到某个合并后的字符串,一定也存在合法的划分方案能得到相同的字符串。
如果不明白的话可以对下面的这个例子手玩一下:
有了之前的结论,我们就不用再管划分的区间有没有相邻相同字符了,只要管模 \(3\) 不等于 \(0\) 就行,一下子问题变得可做了很多。
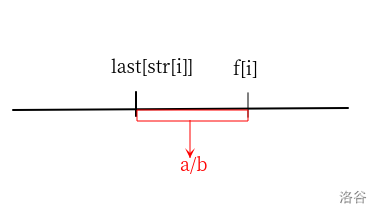
于是我们考虑 DP 计数,设 \(f[i]\) 表示原串 \([1,i]\) 的区间的划分方案数,并且我们要让每种方案合并之后的字符串本质不同。
称原串 \(i\) 的前缀和在 \(\bmod 3\) 意义下为 \(a[i]\)。设当前遍历到 \(i\),我们想在之前已经统计过的方案后面加上一个新段,即从上一个 \(a[j]\neq a[i]\) 的 \(j\) 转移,例如当前 \(a[i]=2\),我们就需要找前面第一个 \(a[j]=1\) 和 \(a[j]=0\) 来转移。\(f[i]+=f[j]\),表示我们在 \(f[j]\) 的基础上再将 \((j,i]\) 这个区间合成为一个字母。然后我们判断 \([1,i]\) 能否被直接缩成一个字符,因为现存的方案在后面接上一个新段后,合并后字母数至少都是 \(2\),所以将 \([1,i]\) 整个缩为 \(1\) 个字母一定是本质不同的。
- 为什么需要 \(a[j]\neq a[i]\)?
如下图,由于 \(a[i]\) 是模 \(3\) 意义下的前缀和,如果 \(a[j]=a[i]\),则说明 \((j,i]\) 这个区间内的字符和为 \(0\),不能缩成一个字符。
【勘误】下图中的 str 应该为 a。
- 为什么是从上一个 \(a[j]\ne a[i]\) 的 \(j\) 转移,而不是上上个?上上上个?……
这样做是为了确保方案之间合并后的字符串本质不同,假如说
babbb,\(i=5\),\(a=[2,0,2,1,0]\),你要是从第一个 \(2\) 转移,即把 \((1,5]\) 这个区间的abbb合并为a,最后得到ba,但我们发现ba早就在 \(i=2\) 的时候就被统计过了。
可以发现,这样转移是不会遗漏或多算的。
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL P=1e9+7;
const int MAXN=1e5+5;
int n,a[MAXN],f[MAXN],last[3];
string str;
int main(){
cin>>str;
n=str.size();
bool flag=1;
for(int i=1;i<=n;i++){
a[i]=(str[i-1]=='a'?1:2);
if(i>1 && str[i-1]==str[i-2]) flag=0;
}
if(flag){
puts("1");
return 0;
}
for(int i=1;i<=n;i++){
a[i]=(a[i]+a[i-1])%3;
}
for(int i=1;i<=n;i++){
f[i]=(int)(a[i]>=1);
for(int j=0;j<3;j++){
if(j!=a[i]) f[i]=(f[i]+f[last[j]])%P;
}
last[a[i]]=i;
}
cout<<f[n]<<endl;
return 0;
}