NFLS 231031 比赛总结
T1 蛋糕(JOI2014Final)
题面：给你一个环形，给你 \(n(n\leq1e5)\) 个切口以及两两切口之间环的面积 \(A_i\)，你需要选择 \(3\) 个切口切下将环分成三段，使得三段面积的最小值最大。
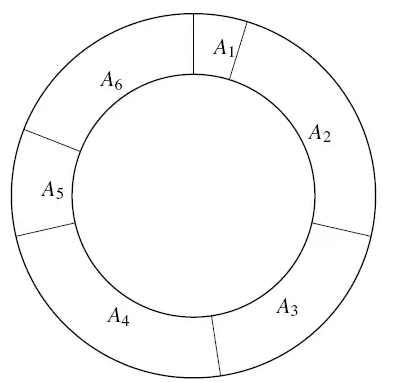
思路：首先由于是环我们不难想到要破环成链，\(O(n)\) 枚举每一种断环方式，二分查找这个最大的最小值，在 check 时，我们在链上再进行两次二分找到两个最小的面积大于 \(mid\) 的段，判断剩下的那个段面积是否大于 \(mid\) 即可。
总结：刚拿到题时一直在想如何做到 \(O(n)\) 枚举第一个切口然后 \(O(\log_n)\) 统计剩下两个切口的答案，却忽略了最重要的“最小值最大”这类经典套路。本题很难做到 \(O(\log_n)\) 的统计答案，但是如果我们逆向思维来看，完全可以做到用二分来寻找答案并在 \(O(\log_n)\) 的复杂度内 check 答案。
代码：
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e5+5;
typedef long long LL;
int n,n2,a[MAXN<<1],st,ed;
LL sum=0,ANS=0,pre[MAXN<<1];
inline bool check(LL x){
int l=st,r=ed,mid;
while(l<r){
mid=(l+r)/2;
if(pre[mid]-pre[st-1]>=x) r=mid;
else l=mid+1;
}
if(r==ed) return false;
int k=r;
l=k+1;r=ed;
while(l<r){
mid=(l+r)/2;
if(pre[mid]-pre[k]>=x) r=mid;
else l=mid+1;
}
if(r==ed) return false;
return pre[ed]-pre[r]>=x;
}
int main(){
freopen("cake.in","r",stdin);
freopen("cake.out","w",stdout);
cin>>n;
n2=n*2;
for(int i=1;i<=n;i++){
cin>>a[i];
a[i+n]=a[i];
sum+=a[i];
}
pre[0]=0;
for(int i=1;i<=n2;i++){
pre[i]=pre[i-1]+a[i];
}
for(st=1;st<n;st++){
ed=st+n-1;
// cout<<st<<' '<<ed<<endl;
LL l=1,r=sum/3,mid,ans=0;
while(l<=r){
mid=(l+r)/2;
// cout<<mid<<' ';
if(check(mid)){
ans=mid;
l=mid+1;
// cout<<"Y"<<endl;
}
else{
r=mid-1;
// cout<<"N"<<endl;
}
}
ANS=max(ANS,ans);
// cout<<endl;
}
cout<<ANS<<endl;
return 0;
}
/*
6
1 5 4 5 2 4
*/
T2 Chefina 与区间
题面：给你 \(n(n\leq1e5)\) 个区间，请你将这些区间分为两个非空的集合，满足两个有交的区间一定在同一集合中，你可以从中删除一些区间，问至少要删几个区间才能满足要求，如果无论如何都不能满足要求输出 \(-1\)。
思路：我们推一下性质，发现对于一种情况，只要极大的区间并数量大于等于二，该情况即符合要求。那么我们就可以枚举每个点，删掉覆盖了该点的每个区间后判断合法（该点左右是否有还剩有区间），如合法就统计答案。具体实现我们还可以进一步优化，我们 \(O(n)\) 求出对于某个点，右端点小于等于该点的区间的数量 \(bef[i]\)，以及反过来，左端点大于该点的区间的数量 \(aft[i]\)，然后再 \(O(n)\) 枚举分界点，如果这个点左右区间数量都不为 \(0\)，那么即合法，更新答案 \(n-bef[i]-aft[i]\)。
总结：以为是一道 DS 题，一上来就想到一个假的性质，手算小样例过后没多想就开写线段树了，写完测大样例发现错了，重新思考了一下立即就找到了反例。虽然这次没耽误太多时间，但这样的鲁莽做法不可取，万一下次不是线段树是 Splay 怎么办？所以想出性质后还是应该花几分钟想办法证明或者找反例证伪，避免浪费时间。
代码：
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e5+5,MAX2N=MAXN<<1;
typedef pair<int,int> pii;
int n,buck[MAX2N],len,ans,d[MAX2N],bef[MAX2N],aft[MAX2N];
pii co[MAXN];
inline void checkmin(int& x,int v){
if(x==-1) x=v;
x=min(x,v);
}
int main(){
freopen("chfran.in","r",stdin);
freopen("chfran.out","w",stdout);
int t;
cin>>t;
while(t--){
ans=-1;
cin>>n;
for(int i=1;i<=n;i++){
cin>>co[i].first>>co[i].second;
buck[i]=co[i].first;
buck[i+n]=co[i].second;
}
sort(buck+1,buck+1+2*n);
len=unique(buck+1,buck+1+2*n)-buck-1;
for(int i=1;i<=n;i++){
co[i].first=lower_bound(buck+1,buck+1+len,co[i].first)-buck;
co[i].second=lower_bound(buck+1,buck+1+len,co[i].second)-buck;
// cout<<co[i].first<<' '<<co[i].second<<endl;
}
memset(d,0,sizeof(d));
for(int i=1;i<=n;i++){
d[co[i].second]++;
}
bef[0]=0;
for(int i=1;i<=len;i++){
bef[i]=bef[i-1]+d[i];
}
memset(d,0,sizeof(d));
for(int i=1;i<=n;i++){
d[co[i].first]++;
}
aft[len+1]=0;
for(int i=len;i>=1;i--){
aft[i]=aft[i+1]+d[i];
}
for(int i=1;i<=len;i++){
if((bef[i]!=0) && (aft[i+1]!=0)){
checkmin(ans,n-bef[i]-aft[i+1]);
}
}
cout<<ans<<endl;
}
return 0;
}
