区间和线段树的各种操作

这篇文章我们来讲一下线段树

线段树，适用于对一个数列区间进行操作，可以求这段数列\(i\)到\(j\)的和、乘积、最大值、最小值等等等等，因此线段树有十分多的变种

问题提出

如果我给你一个数列\(a\)，要求你把\(a_i\)到\(a_j\)中所有的值全部加上\(k\)，并最后输出某些区间所有数的和

解决方案

最朴素的做法就是遍历从\(i\)到\(j\)全部加一遍，如果\(a\)最多有\(n\)个元素，操作次数为\(m\)，那么此时最坏复杂度为\(O(nm)\)，而有些题目恰好卡这类数据，怎么办呢？

那我们换一种思路，我们将对于某个区间的和全部存下来，区间\(i\)到\(j\)加上\(k\)时，我们就\(sum[i,j]+=k\)，先将对于某个区间修改存下来，而不将该修改直接实施在数列中的数上，而当我们询问到某个区间的值或某一个数修改后的值时，再将对它的操作递归累加下来，这样就快得多。

按刚才的说法，时间复杂度降下来了，但空间复杂度为\(O(n^2)\)，那么我们继续优化——有必要枚举所有区间吗？其实是没必要的，我们可以用二分的思想，如果区间太大了，我们就二分，切成两个子区间，继续下去……搜到合适的存储单元并囊括整个区间，将修改值累加上去；如果区间太小了，那么我们就像二分搜索一样由大到小搜到合适的区间，并将修改值累加……这么说很抽象，那么我们试图将这种数据结构画下来……

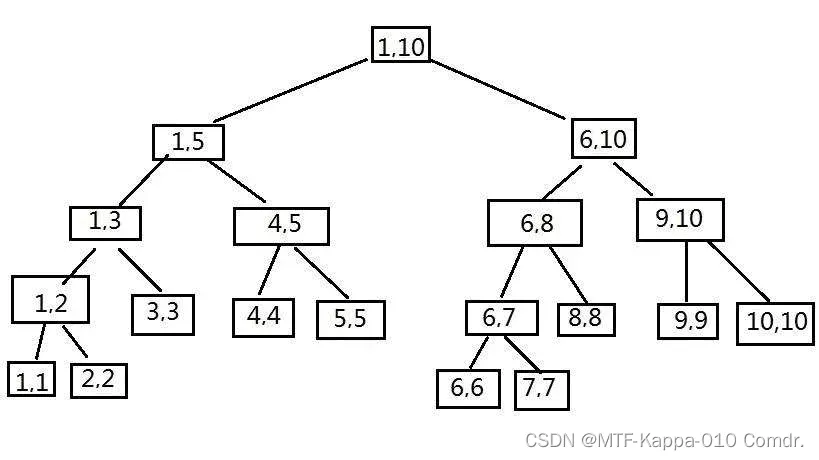
你发现了吗？没错，就是一棵树嘛！这就叫线段树

验证解法

那我们现在模拟一下线段树的操作过程

1 给出一个数列\(1,2,3,...,10\)（注意举例1到10只是为了方便，区间与存储的数据没有关系，上图中的数对是区间，不要混淆！）
2 将区间6,8中的数全部加上2
3 将区间2,5中的数全部加上1
4 输出区间6,10中所有数的和
5 输出区间1,4中所有数的和

1. 初始化线段树（红色的数为区间和）
   
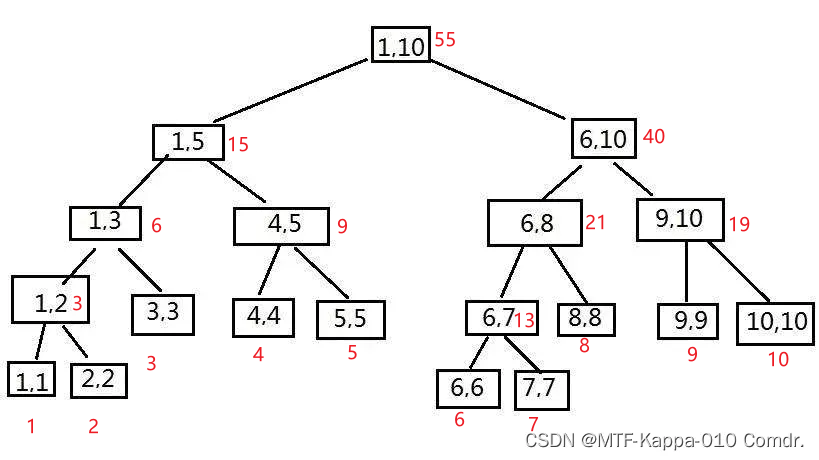
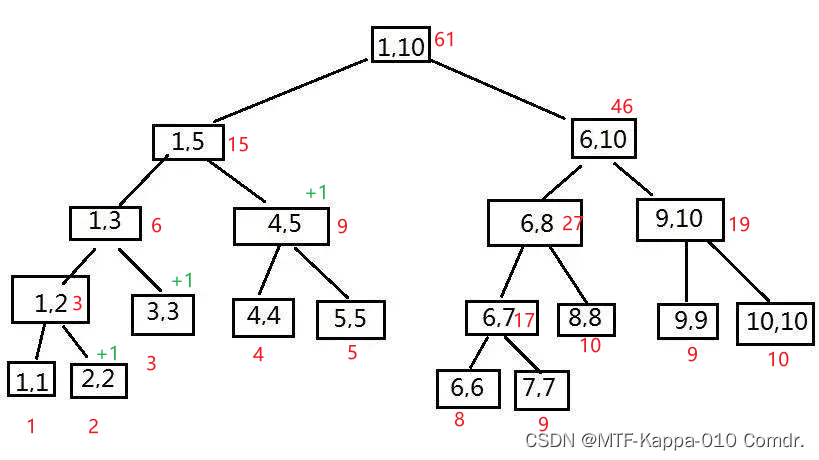
2. [6,8]每个数+2（绿色的数为修改标记）
   
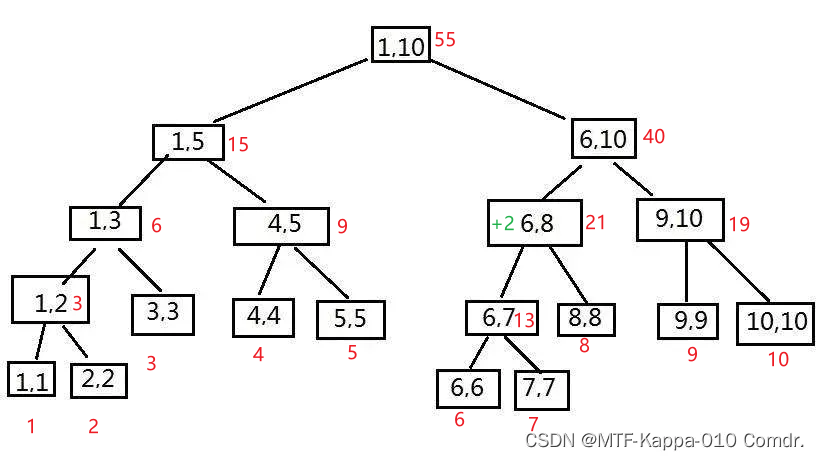
3. [2,5]每个数+1
   
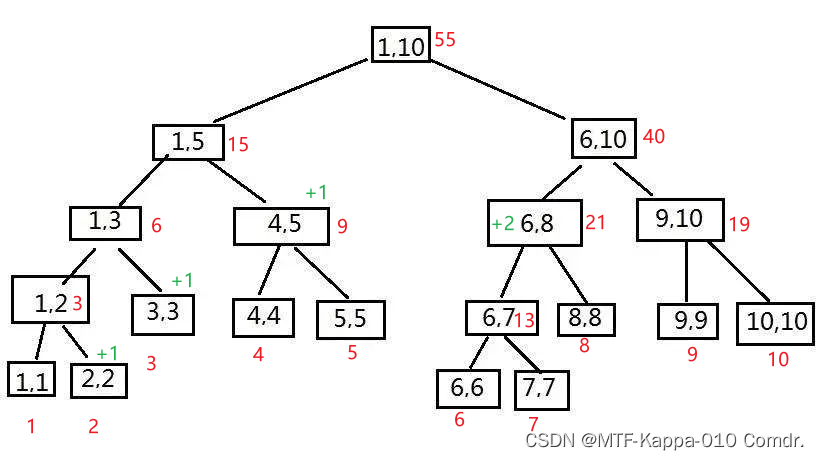
4. 输出[6,10]区间和（没涉及的地方不用更新数值，节省时间） 输出46
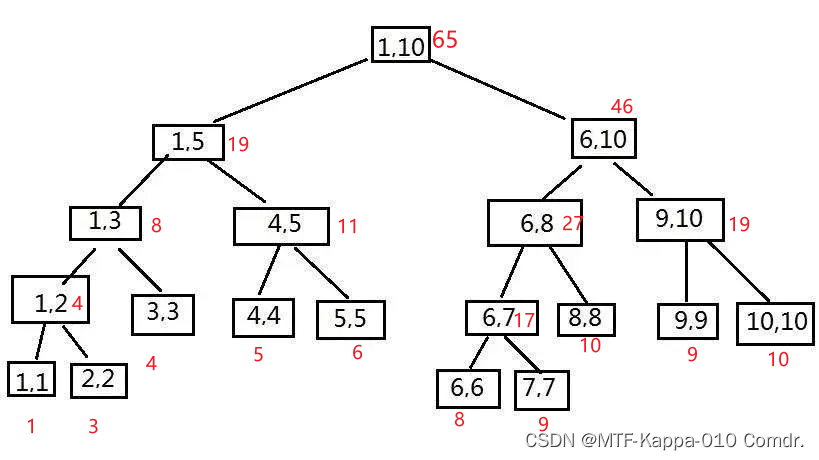
   6. 输出[1,4]区间和 输出[1,3]+[4,4]=13
   

---

代码实现

我们将这些操作变成一个个函数
分别是

• build() 初始化线段树
• push_down() 将某个区间的修改标记实现到每一个区间内的数上
• push_up() 修改完成后需要重新计算区间和，递归上去
• query() 查询某个区间的区间和
• update() 区间修改
• change() 单点修改

#include<bits/stdc++.h>
#define LL long long
using namespace std;
const int MAXN=1e5+10;
int m,n,arr[MAXN];
LL sum[MAXN<<2],add[MAXN<<2]={0};//数列长度为n，总共最多有4n个节点
void push_up(int pos){
	sum[pos]=sum[pos<<1]+sum[(pos<<1)+1];
}
void push_down(int pos,int len){
	if(add[pos]>0){
		add[pos<<1]+=add[pos];
		add[(pos<<1)+1]+=add[pos];
		sum[pos<<1]+=add[pos]*(len-len/2);
		sum[(pos<<1)+1]+=add[pos]*(len/2);
		add[pos]=0;
	}
}
void build(int l,int r,int pos){
	if(l==r){
		sum[pos]=arr[l];
		return;
	}
	int mid=(l+r)/2;
	build(l,mid,pos<<1);
	build(mid+1,r,(pos<<1)+1);
	push_up(pos);
}
void update(int SecL,int SecR,LL AddV,int NowL,int NowR,int pos){
	if(SecL<=NowL && NowR<=SecR){
		add[pos]+=AddV;
		sum[pos]+=(LL)(AddV*(NowR-NowL+1));
		return;
	}
	push_down(pos,NowR-NowL+1);
	int mid=(NowL+NowR)/2;
	if(SecL<=mid){
		update(SecL,SecR,AddV,NowL,mid,pos<<1);
	}
	if(mid+1<=SecR){
		update(SecL,SecR,AddV,mid+1,NowR,(pos<<1)+1);
	}
	push_up(pos);
}
LL query(int SecL,int SecR,int NowL,int NowR,int pos){
	if(SecL<=NowL && NowR<=SecR){
		return sum[pos];
	}
	push_down(pos,NowR-NowL+1);
	int mid=(NowL+NowR)/2;
	LL ans=0;
	if(SecL<=mid){
		ans+=query(SecL,SecR,NowL,mid,pos<<1);
	}
	if(mid+1<=SecR){
		ans+=query(SecL,SecR,mid+1,NowR,(pos<<1)+1);
	}
	return ans;
}
void change(int l,int r,int x,int pos,int v){
	if(r<x||l>x) return;
	if(l==r&&l==x){
		sum[pos]+=v;
		return;
	}
	int mid=(l+r)/2;
	change(l,mid,x,pos<<1,v);
	change(mid+1,r,x,(pos<<1)+1,v);
	push_up(pos);
}
int main(){
	cin>>n>>m;//n个数m个操作
	for(int i=1;i<=n;i++){
		cin>>arr[i];//输入初始数列
	}
	build(1,n,1);//建树，区间1到n
	//余下输入部分因题而异
	return 0;
}