各大排序算法的优缺点以及实现方法
这篇文章,我们来谈谈一些关于排序的东西
注意!这篇文章在写的时候混淆了一个概念,“稳定”本义指的是能保证两个相等的数,经过排序之后,序列的前后位置顺序不变。在本文中理解成了排序的复杂度是否固定!!!望读者分辨清楚!!!
排序是什么?
排序是什么?我们首先要来解决一下这个问题。
排序,就是把一串数字(程序里就是数组)内的东西按照一定的规律来调整顺序。
排序的目的是将一组“无序”的记录序列调整为“有序”的记录序列。
【正题】排序算法是哪些?长什么样?怎么实现?
知道了排序的意义,我们来了解一下排序的种类有哪些。
-
冒泡排序 BUB
冒泡排序的意思有点像一次次的交换,把最大/最小的量一次次“推”到最后。
它是这样实现的:
1.从头遍历到尾(a[1]到a[n]),把a[1]与a[2]作对比,如果a[1]大于/小于a[2]那么就要把两者交换(swap(a[1],a[2]));再把a[2]与a[3]作对比,如果a[2]大于/小于a[3]那么就要把两者交换;以此类推……直到比较到a[n-1]与a[n],那么此时的a[n]肯定是最大/最小的了。
2.然后再来一轮,从头遍历到尾(a[1]到a[n]),把a[1]与a[2]作对比;再把a[2]与a[3]作对比;
以此类推……
直到最后一轮:值得注意的是,这次只比较到a[n-2]与a[n-1](因为a[n]已经是最大/最小的了,不用比较a[n]),那么此时的a[n-1]肯定也是最大/最小的了。
这样子说可能有点绕,让我们看动图(黄色是已被排序的,绿色是正在比较中的):
素材来自VisuAlgo
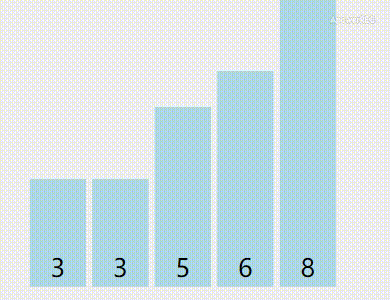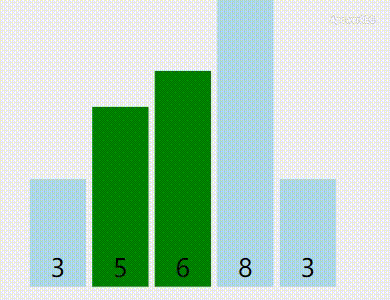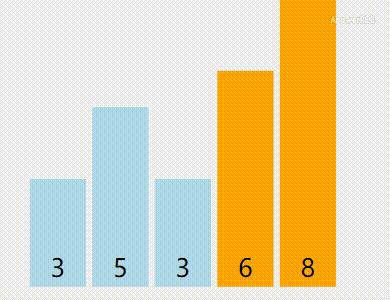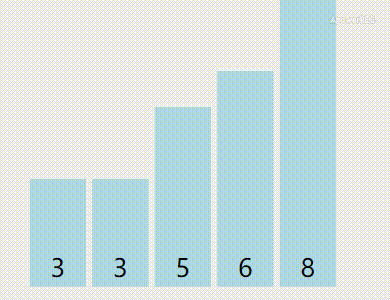
算法优点:稳定
算法缺点:所需时间太长,时间复杂度高,接近O(n²)
冒泡排序理论上总共要进行n(n-1)/2次交换 -
选择排序 SEL
选择排序比冒泡排序好理解一些。
它是这样实现的:
1.从头遍历到尾,找到其中的最小值,并把这个值与第一个没排序过的量交换。
2.然后再来一轮,从第二个量遍历到尾(a[2]到a[n]),因为此时第一个量已经被排序过了。
以此类推……
来个图(红色是当前最小值,黄色是已被排序的,绿色是比较中的):
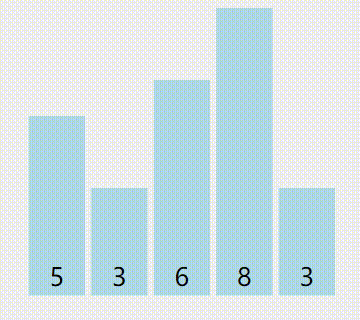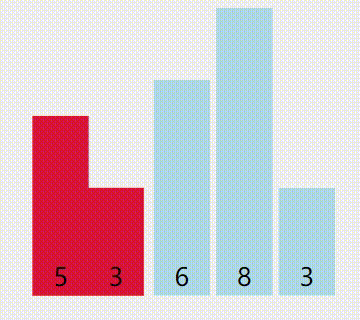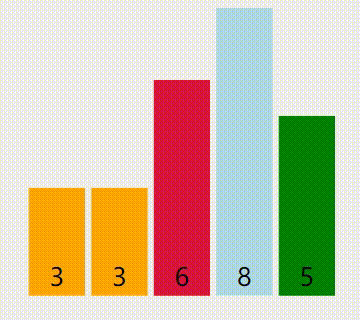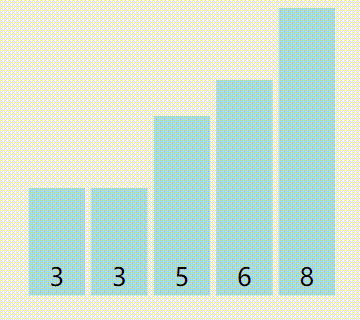
算法优点:移动数据的次数已知。
算法缺点:比较次数多,不稳定。
选择排序总共要进行n-1次交换 -
插入排序 INS
插入排序是这样实现的:
1.将第一个量标记为已排序。
2.然后把第一个没有排序过的量提取出来,一个一个往前寻找,直到找到一个比它小/大的量,然后插入在它后面。
3.然后再来一轮,重复第二步即可。
以此类推……
再来个图(红色是提取的待插入值,黄色是已被排序的,绿色是与红色比较的):
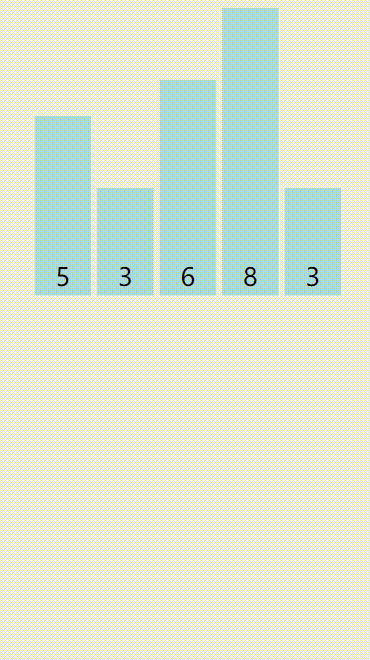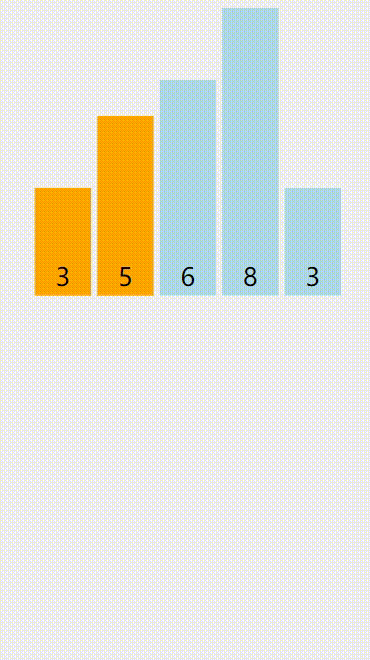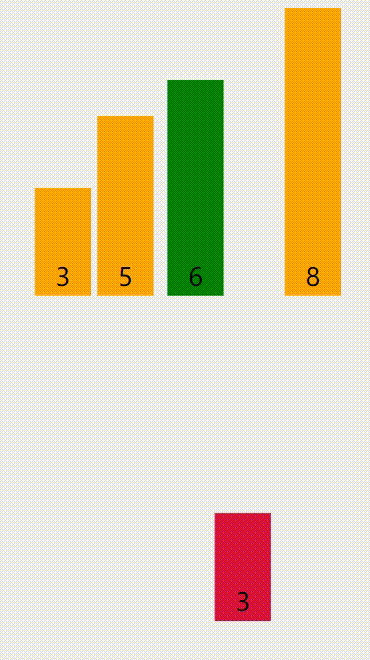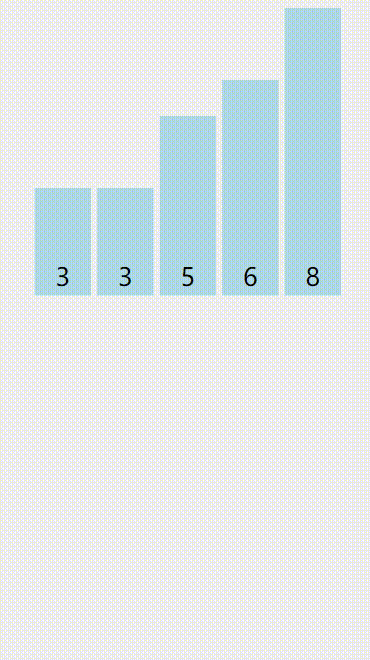
算法优点:稳定,快。
算法缺点:比较次数不一定,比较次数越多,插入点后的数据移动越多(特别是当数据总量庞大的时候)。但用链表可以解决这个问题。
最好情况:序列已经是期望顺序了,在这种情况下,需要进行的比较操作需(n-1)次即可。
最坏情况:序列是期望顺序的相反序列,那么此时需要进行的比较共有n(n-1)/2次。
插入排序算法的时间复杂度平均为O(n^2) -
归并排序 MER
归并排序就是把元素分为各个部分,让它们组合成有顺序的部分,最后一步步地组成一个整体,这就排完序了。
归并排序这其实让我也思考了很久:到底怎么给大家讲明白呢?
最后我想到一个非常贴切的例子:2048
大家想必都玩过2048这款游戏吧,游戏规则就是把相同的数字相组合,可以斗出一个更大的数(把两数相加)。
而归并排序也很像这款游戏,游戏中的数字就是我们归并部分的长度,唯一不同的地方在于:游戏中数字从2开始,而归并单位的长度初始为1,并且它也只能把相同长度的部分相组合(当然,除了最后一部分,长度为奇数时就无法拼凑完整)。
归并排序是这样实现的:
1.首先将每个元素拆分成大小为1的部分。
2.然后我们就把最前面的两个部分归并,归并步骤如下:- 把两个部分的第一个数字相比较,把当中的最大/最小值抽出来(意思原来的部分的第一个数被删了,第二个来接替,整体往前挪,有点像队列),进入临时队列当中
- 再次进行第一步
以此类推,直到原来的两个部分都没有数了为止,再把临时队列当中的数依次放回原数组
3.然后再来一轮,重复第二步即可。
以此类推……直到只剩下一个部分,组成一个整体。
大家配合下面的动图理解一下(不同的颜色代表不同的部分):
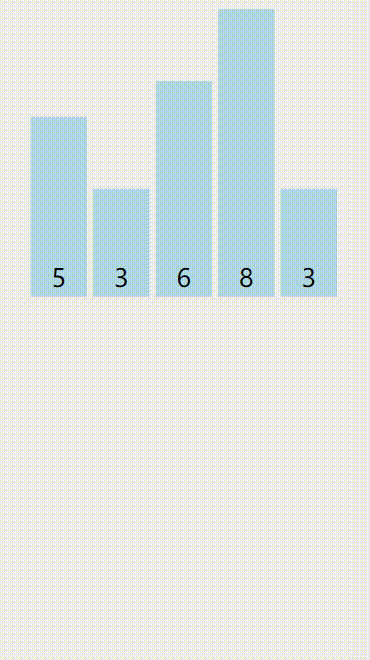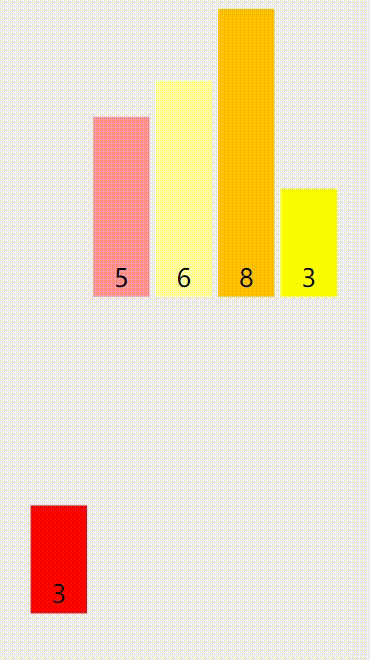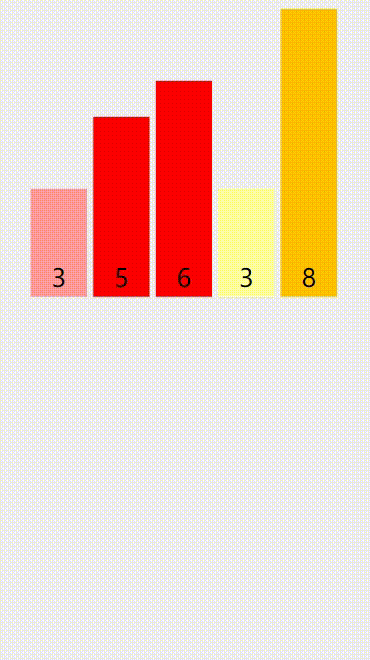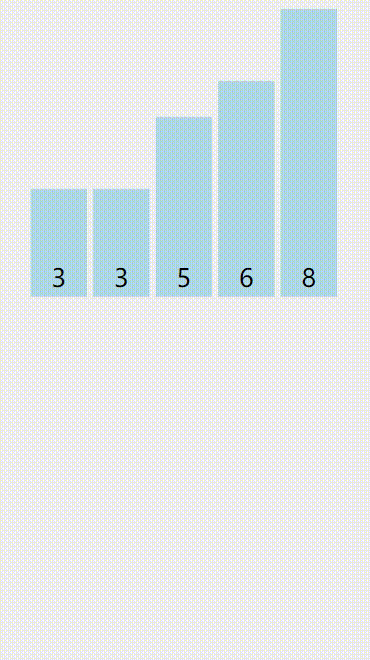
算法优点:稳定,快。
算法缺点:空间复杂度太高,为O(n)。 没办法,只能以空间换时间
归并算法的时间复杂度平均为O(nlog2n) -
计数排序 COU
计数排序是这样实现的:
1.开一个数组,数组长度为排序数据的最大值与排序数据最小值的差+1。
2.初始化数组,使得数组的每一个值都为0。
3.每处理一个数据,就再以这个数为下标的数组单元+1。(输入进来n,a[n]++)
4.再把数组从头到尾遍历一遍,遇到一个数组单元就输出数组存储的数个 数组下标。(循环i=1~n 每次输出a[i]个i)
又来个图:
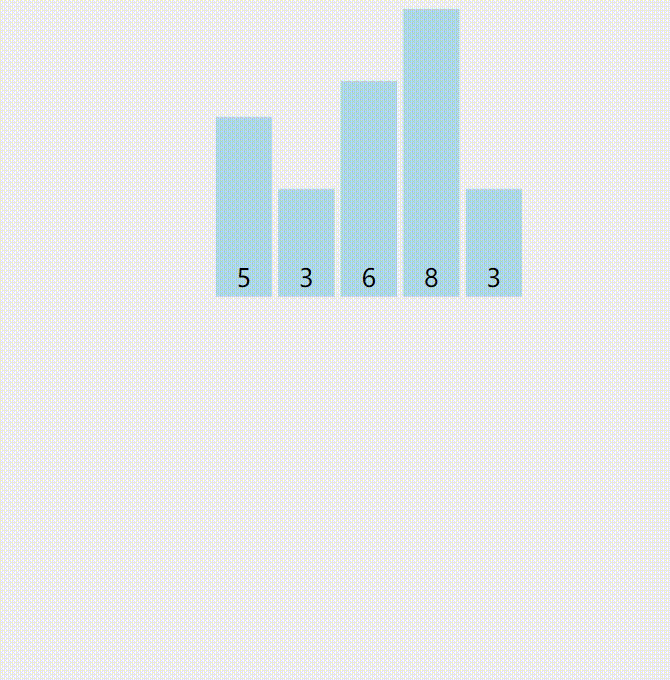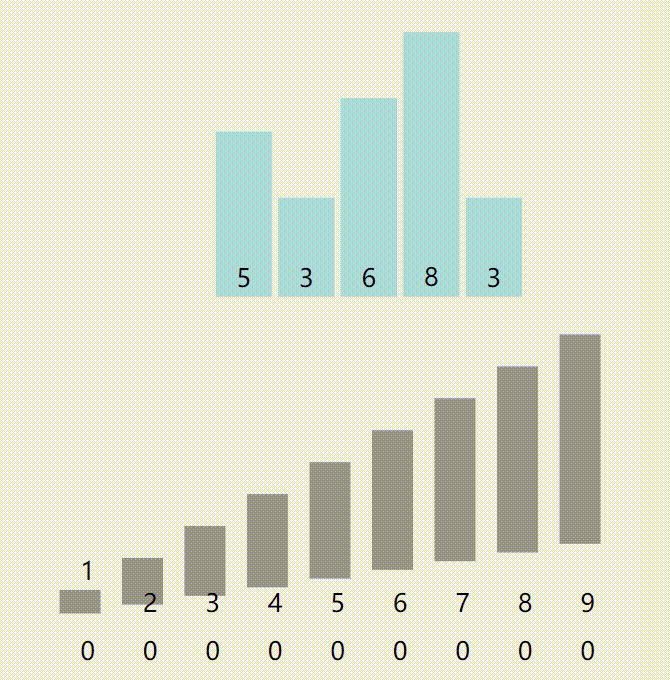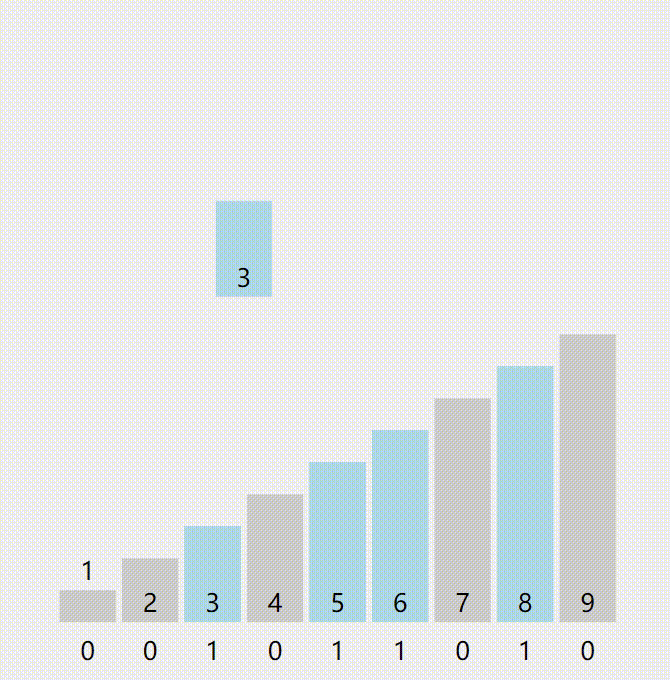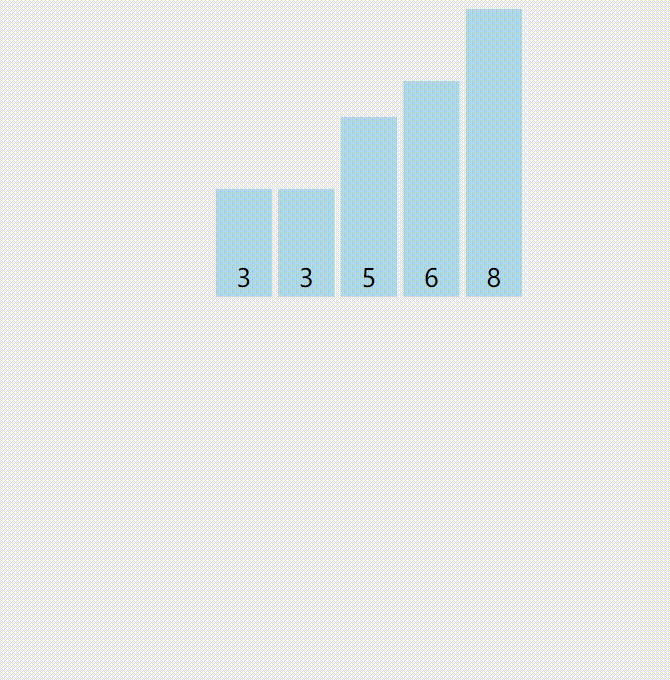
算法优点:快。
算法缺点:太太太太太耗内存了内存:“我做错了什么???”
最好情况: 空间复杂度非常高,且浪费的空间异常之多。排序数据的最大值有多少,它就得开多大的空间。
计数排序算法的时间复杂度平均为O(2n)
计数排序只适合处理小数据,不适合处理排列稀疏的大数据!!! -
基数排序/桶排序/箱排序 COU
不适用于负数!!!
“基数排序”与“计数排序”仅一字之差,却大相径庭!前面我们说过,计数排序只适合处理小数据,而计数排序恰恰适合处理位数很多的大数据,一定要注意这个“位数很多”。别急,等我讲完了你就明白了。
基数排序是把数的位数(个、十、百、千、万……)全部分割开来,从小位数到大位数遍历,把他们按照当前遍历到的位数上的数字分别放到10个队列中,分数为遍历排序。
基数排序是这样实现的:
1.开10个队列,队列代表着为0~9。
2.第一轮处理个位,每处理一个数据,就把这个数入代表这个数个位的队列中去,然后再一个个从代表0的队列到代表9的队列依次出队。
3.第二轮处理十位,每处理一个数据,就把这个数入代表这个数十位的队列中去(没有十位算十位为0),然后再一个个从代表0的队列到代表9的队列依次出队。
以此类推……直到所有数的最高位。
最后就可以得到排好序的队列了
以上方法是求升序的方法,那么求降序的方法请朋友们自己好好动脑筋思考!Answer:从代表9的队列到代表0的队列依次出队就可以了
示意动图:

有朋友会发现我们没有再使用之前的 5 3 6 8 3 为例子了,其实我是故意这样的,这样正好体现了基数排序适合处理位数很多的数据的特点!!!
算法优点:稳定,空间复杂度永远是O(10n)。
算法缺点:这是个比较中性的算法,没什么缺点
基数排序算法的时间复杂度为O(n)级(注意是“级”,因为它的时间复杂度变动幅度很大) -
快速排序 QUI
最厉害的当然是压轴啦!
快速排序(Quicksort)是对冒泡排序的一种改进。
作者认为这个比较难理解,请认真学习快排
快速排序是这样实现的:
1.将第一个没遍历过的元素设为轴心点。
2.再往后遍历没遍历过的元素,标记好小于等于轴心元素的与大于轴心元素的。
3.把轴心点放在最后一个小于等于轴心元素的元素的后面,第一个大于轴心元素的元素的前面,并把轴心点标记为已经遍历过的元素。
重复以上步骤,直到所有的元素都被标记为已经遍历过的元素
这是示意图(浅黄色是轴心点,黄色是已被排序的,绿色是小于等于轴心的,紫色是大于轴心的,红色是正在比较中的):
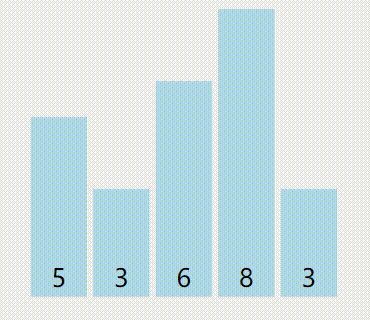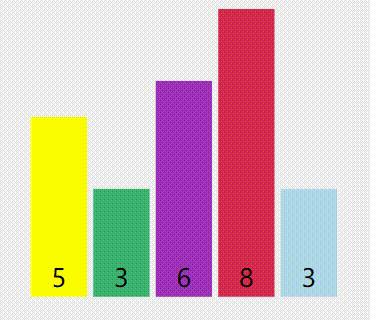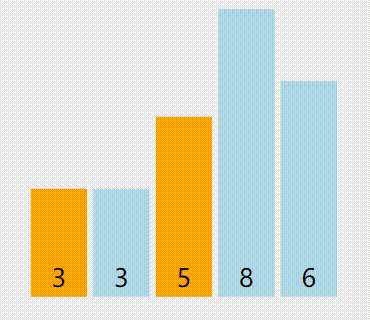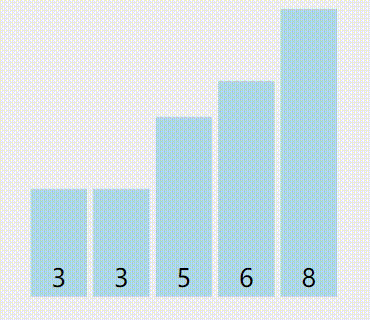
算法优点:用空间很少,用时一般很少,可谓是在时间复杂度和空间复杂度上找到了“平衡点”
算法缺点:非常不稳定
最好情况:时间复杂度:O(nlog2n)
最坏情况:时间复杂度:O(n^2)
快速排序算法的时间复杂度平均为O(nlog2n)
一些简单的做法
让我们学习一些简单的做法吧:
sort函数
这个函数的原型长这个样:
sort(start,end,cmp)
start表示要排序数组的起始地址;
end表示数组结束地址的下一位;
cmp用于规定排序的方法,可不填,默认升序。
sort函数用于C++中,对给定区间所有元素进行排序,默认为升序,也可进行降序排序。sort函数进行排序的时间复杂度为n*log2n,比冒泡之类的排序算法效率要高,sort函数包含在头文件为#include<algorithm>的c++标准库中。
比如说,我输入了n个数,存在数组arr当中,我想按升序排列(从a[1]开始输入),该怎么调用sort呢?
这样就可以了:
int main()
{
int n;
int arr[100];
cin>>n;
for(int i=1;i<=n;i++){
cin>>arr[i];
}
sort(arr+1,arr+1+n);//arr+1指的是a[1]的地址,arr+1+n同理
for(int i=1;i<=n;i++){
cout<<arr[i];
}
return 0;
}
但,如果我想以降序输出,怎么办呢?
有2种办法:
第一种:直接反过来输出。。。
int main()
{
int n;
int arr[100];
cin>>n;
for(int i=1;i<=n;i++){
cin>>arr[i];
}
sort(arr+1,arr+1+n);//arr+1指的是a[1]的地址,arr+1+n同理
for(int i=n;i>=1;i--){
cout<<arr[i];
}
return 0;
}
第二种:运用cmp
bool cmp(int x,int y){//cmp可以是bool,也可以是int
return x>y;
//x可以理解成前面的数,y 以理解成x后面的数
//升序就是 前面的数<后面的数 所以就是return x<y
//而降序就是 前面的数>后面的数 所以就是return x>y
}
int main()
{
int n;
int arr[100];
cin>>n;
for(int i=1;i<=n;i++){
cin>>arr[i];
}
sort(arr+1,arr+1+n,cmp);
for(int i=n;i>=1;i--){
cout<<arr[i];
}
return 0;
}
有人会说了:为什么还要学第二种方法呢?第一种比第二种简单多了!
但事实是这样的:如果你要给结构体struct排序,sort就不知道你要以哪个量为基准来排序了!
如果你要给结构体struct排序,请这样写:
struct Node{
int a,b;
}arr[100];
bool cmp(Node x,Node y){
return x.a<y.b;//同理,这是升序
}
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++){
cin>>arr[i].a>>arr[i].b;
}
sort(arr+1,arr+1+n,cmp);
for(int i=n;i>=1;i--){
cout<<arr[i].a<<' '<<arr[i].b<<endl;
}
return 0;
}
并且,这样写的好处是,结构体里的所有量也会跟着“捆绑在一起”排序,像上面代码里的arr,虽然以a作为基准排序,但b也会跟着a一起交换顺序,这可给我们带来了不少便利!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号