树与二叉树的基础概念与代码实现
树与二叉树的基础概念与代码实现
树,其实跟我们现实生活中的树是差不多的。
如果你还不了解树这个数据结构的话,你可能认为树是这样的:
但事实正好相反,在数据结构当中,树的模样是这样的,它更接近于一棵树的根部:
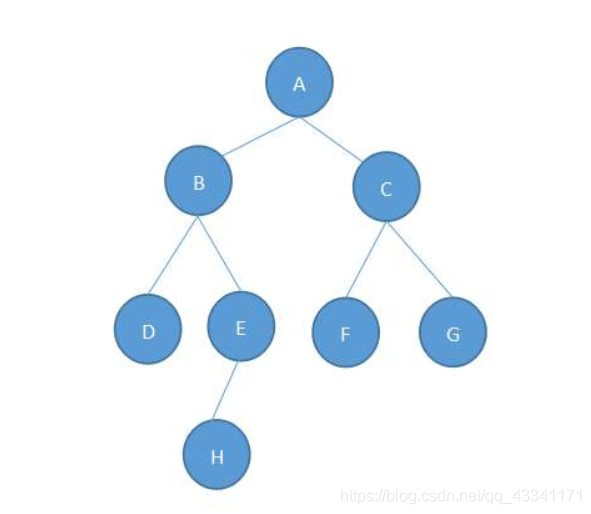
好吧,你现在应该对树有了一个大概的认识,但对它的定义还有些不了解,那么我们来看看度娘的解释吧:
树状图是一种数据结构,它是由n(n>=1)个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:
1.每个结点有零个或多个子结点
2.没有父结点的结点称为根结点
3.每一个非根结点有且只有一个父结点
4.除了根结点外,每个子结点可以分为多个不相交的子树。
要想认识树,我们还需要认识一下树的一些称谓:
空集合也是树,称为空树。空树中没有结点。
★结点的度:一个结点含有的子结点的个数称为该结点的度;
★叶结点或终端结点:度为0的结点称为叶结点;
★非终端结点或分支结点:度不为0的结点;
★双亲结点或父结点:若一个结点含有子结点,则这个结点称为其子结点的父结点;
★孩子结点或子结点:一个结点含有的子树的根结点称为该结点的子结点;
★兄弟结点:具有相同父结点的结点互称为兄弟结点;
★树的度:一棵树中,最大的结点的度称为树的度;
★结点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推;
★树的高度或深度:树中结点的最大层次;
★堂兄弟结点:双亲在同一层的结点互为堂兄弟;
★结点的祖先:从根到该结点所经分支上的所有结点;
★子孙:以某结点为根的子树中任一结点都称为该结点的子孙。
★森林:由m(m>=0)棵互不相交的树的集合称为森林。
这样说可能还不太直观,让我用一张图来解释一下这些概念:
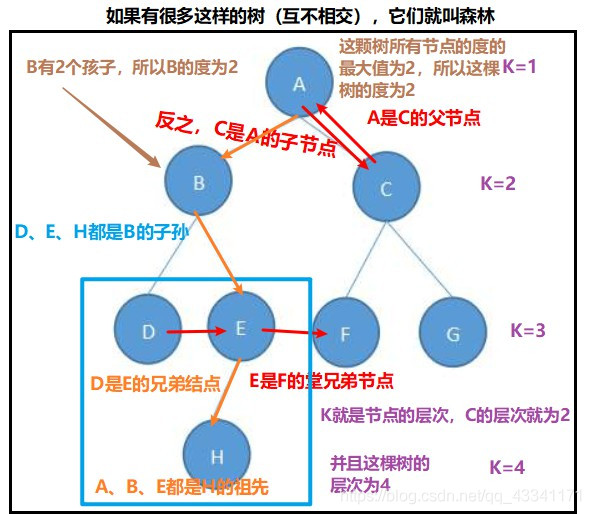
接下来讲讲树的分类,树分为这两类:
- 无序树:这种就是任意的树,没有顺序
- 有序树:这种就是有顺序的树,按照某种顺序排列(堆就是一种有序树)
学习完了树的分类,我们来学学一种非常著名的树:二叉树
所谓一个树是几叉树,其实就取决于这棵树的度。
二叉树,顾名思义就是度为2的树。(按此定义当然也有三叉树、四叉树等等)
给大家放张二叉树的图:
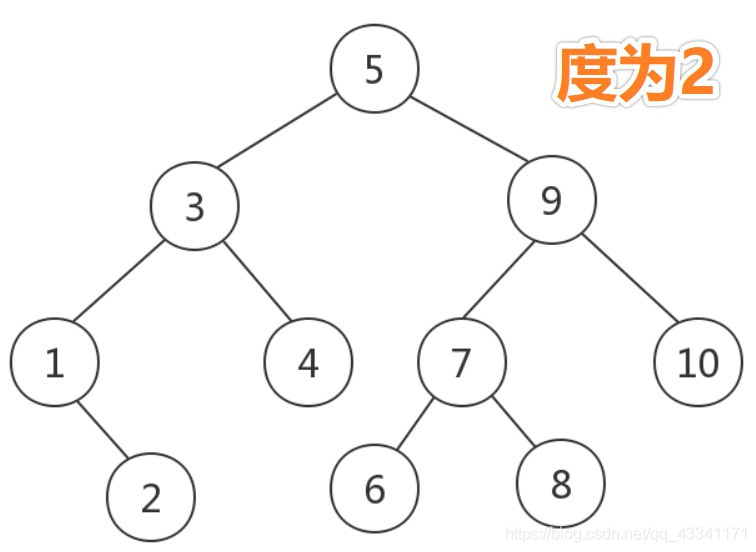
那么,我们再看看二叉树又有哪些分类呢?
- 普通二叉树
- 满二叉树
- 完全二叉树
满二叉树:
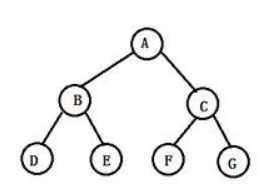
满二叉树的每一个层的结点数都达到最大值,每个节点(除了叶节点)的度都是2。
完全二叉树:
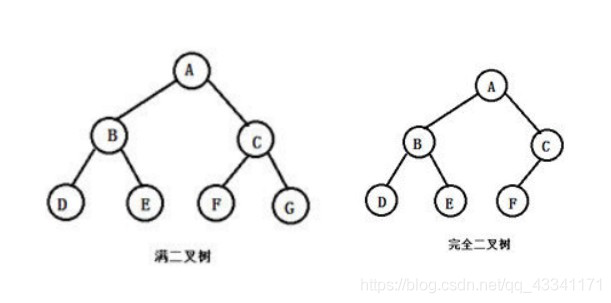
度娘解释:
完全二叉树的每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应。
完全二叉树来自于满二叉树。如果我们将完全二叉树与满二叉树重合,可以发现完全二叉树的节点编号与满二叉树的节点编号一一对应(如上图),只是在最后面可以少一些,但前面一个都不能少。
二叉树特性:
那么,比较全面地认识到了树/二叉树之后,我们来看看二叉树的一些基本操作吧!
-
二叉树的前中后续遍历
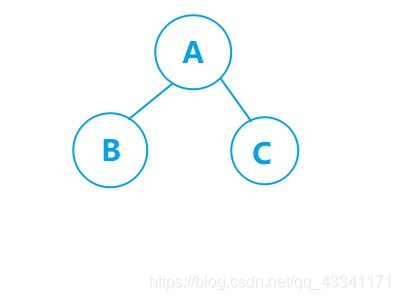
这是一个非常简单的二叉树,只有3个节点。那么我们该怎么遍历它呢?
有3种遍历顺序:
第一种:前序遍历/先序遍历/先根序遍历
这种顺序是按照 根-左-右 的顺序遍历,当我们遍历到一个节点时,先遍历它自己(以自己为根的子树的根),然后遍历它的左孩子,然后遍历右孩子。(没有就不遍历)。
以上图为例遍历结果为:A-B-C第二种:中序遍历/中根序遍历
这种顺序是按照 左-根-右 的顺序遍历,当我们遍历到一个节点时,先遍历它的左孩子,然后遍历它自己,然后遍历右孩子。(没有就不遍历)。
以上图为例遍历结果为:B-A-C第三种:后序遍历/后根序遍历
这种顺序是按照 左-右-根 的顺序遍历,当我们遍历到一个节点时,先遍历它的左孩子,然后遍历右孩子,然后遍历它自己。(没有就不遍历)。
以上图为例遍历结果为:B-C-A那么我们把难度加大,再来一个二叉树,试着用3种遍历顺序遍历一下吧!
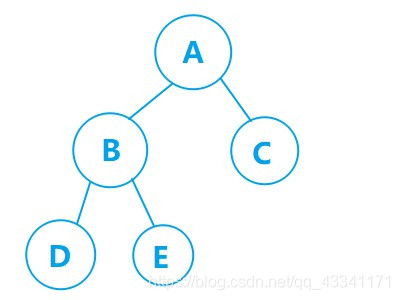
Answer:
前序遍历:A-B-D-E-C
中序遍历:D-B-E-A-C
后续遍历:D-E-B-C-AOK,那么我们已经把二叉树的前中后序遍历学完了,接下来看看代码是如何实现的吧!
#include<bits/stdc++.h>
using namespace std;
int n;
int ls[100]={0},rs[100]={0};//ls左孩子,rs右孩子
void f(int res)//first前序遍历
{
if(res==-1) return;//访问到了叶子节点的孩子(不存在)了
cout<<res<<' ';
f(ls[res]);
f(rs[res]);
}
void m(int res)//mid中序遍历
{
if(res==-1) return;//访问到了叶子节点的孩子(不存在)了
m(ls[res]);
cout<<res<<' ';
m(rs[res]);
}
void l(int res)//last后序遍历
{
if(res==-1) return;//访问到了叶子节点的孩子(不存在)了
l(ls[res]);
l(rs[res]);
cout<<res<<' ';
}
int main()
{
int father;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>father;//父节点
cin>>ls[root]>>rs[root];//输入左孩子和右孩子
}
f(1);
cout<<endl;
m(1);
cout<<endl;
l(1);
return 0;
}
2.求树的节点数:
int cnt(int root)
{
if(root==-1) return 0;
int sum=0;
sum+=cnt(ls[root]);//访问左孩子
sum+=cnt(rs[root]);//访问右孩子
return sum+1;//加上自己
}
注:为了节省空间,本文章后面的程序一些只给出函数,不给出主程序(主程序大致相同)
3.求树的叶节点数:
int cntleaf(int root)
{
if(root==-1)return 0;
if(ls[root]==-1&&rs[root]==-1)return 1;//root是叶节点
return cntleaf(ls[root])+cntleaf(rs[root]);//把左右孩子的结构加起来
}
4.求树的深度
int tdep(int root)
{
if(root==-1) return 0;//搜到叶节点了
int ldep=tdep(ls[root]);//搜左孩子
int rdep=tdep(rs[root]);//搜右孩子
return ldep>rdep?ldep+1:rdep+1;//三元操作符,相当于if(ldep>rdep)return ldep+1;else return rdep+1;
}
5.求数第k层的节点数:
int kcnt(int root,int h)//h是第h层,主程序调时参数为k
{
if(root==-1) return 0;//访问到叶节点了
if(h==1) return 1;//访问到了第k层了
return kcnt(ls[root],h-1)+kcnt(rs[root],h-1);
}
6.判断两棵树结构是否相同
#include<bits/stdc++.h>
using namespace std;
int n,m;
int lsx[100]={0},rsx[100]={0};//第一棵树
int lsy[100]={0},rsy[100]={0};//第二棵树
bool is(int x,int y)
{
if(x==-1&&y==-1) return 1;//结构相同
if(x==-1||y==-1) return 0;//结构不同
return is(lsx[x],lsy[y])&&is(rsx[x],rsy[y]);
}
int main()
{
int root;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>root;
cin>>lsx[root]>>rsx[root];
}
cin>>m;
for(int i=1;i<=n;i++)
{
cin>>root;
cin>>lsy[root]>>rsy[root];
}
//输入
if(is(1,1)) cout<<"True";
else cout<<"False";
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号