loj#6681.yww 与树上的回文串 做题记录
梦里的题目。
像这种路径统计的题目,一般是先点分治,转化为一个连通块统计经过重心的回文路径数量。
然后拼接两条路径,应该是形如这样:
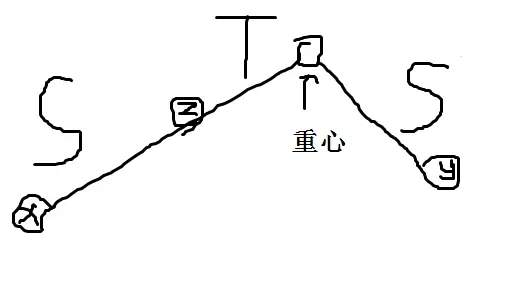
其中 \(T\) 是回文串。思考如何统计,观察到一点:对于所有结点,其到重心的路径上连接起来的字符串中,回文后缀可以被划分为若干个等差数列。这属于回文 Border 理论。
枚举 \(x\),我们需要统计的 \(S\) 长度形如若干个等差数列。对于单个长度的统计也是问题,考虑建立 ACAM,那么就是在 fail tree 上的某个祖先,倍增即可。
对于一个等差数列,不好直接求解。考虑根号分治,若公差 \(d > B\) 则暴力查,否则离线挂到 fail tree 上,贡献差分一下,然后 dfs 一遍 fail tree,实时维护 \(c_{i, j}\) 表示当前点的所有祖先的长度 \(\bmod i = j\) 的数量。
时间复杂度 \(\mathcal O(n ^ {\frac 32} + n\log ^ 3 n)\)。
启示:多观察问题模型,找到合适的解决方法。比如这题观察到 T-S-T 的结构时,需要思考如何统计 S 的信息(回文 Border 理论),以及如何找到对饮的 T(ACAM)。

