Border / 回文 Border 理论小记
普通 Border 理论
- \(\text{定理}(1)\)（弱周期引理）：若 \(p,q\) 是字符串 \(S\) 的两个周期，且 \(p+q\le |S|\)，那么 \(\gcd(p,q)\) 也是 \(S\) 的一个周期。
证明：不妨钦定 \(p<q\)，设 \(d=q-p\)
对于 \(i\in [p+1,|S|]\)，有 \(S_i=S_{i-p}=S_{i-p+q}=S_{i+d}\)。
对于 \(i\in [1,|S|-q]\)，有 \(S_i=S_{i+q}=S_{i+q-p}=S_{i+d}\)。
由 \(p+q\le |S|\)，推得 \(p+1>n-q\)，因此 \(d=q-p\) 也是 \(S\) 的一个周期。
使用更相减损术来归纳，即可得证。
当然有更厉害的强周期引理：若 \(p,q\) 是周期，且 \(p+q-\gcd(p,q)\le |S|\)，那么 \(\gcd(p,q)\) 也是周期。但是用的不多。
- \(\text{定理}(2)\)：对于两个字符串 \(S,T\)，若 \(|S|\le T\le 2|S|\)，那么 \(S\) 在 \(T\) 中的匹配位置是一个等差序列。
证明：我们只需考虑匹配次数 \(\ge 3\) 的情况。
考虑第一、二次匹配距离为 \(d_1\)，第二、三次匹配距离为 \(d_2\)。因为 \(2|S|\ge T\)，三个匹配相邻两两相交，那么 \(d_1,d_2\) 是 \(S\) 的两个周期。
又根据 \(2|S|\ge T\)，第三次匹配的位置 \(\le |T|-|S|+1\le 2|S|-|S|+1=|S|+1\)。
而第一次匹配的位置 \(\ge 1\)，则 \(d_1+d_2\le |S|\)。又知他们都是 \(S\) 的周期，根据弱周期引理，\(r=\gcd(d_1,d_2)\) 也是一个周期。
对于 \(S_{1...d_1}\)，因为 \(r=\gcd(d_1,d_2)|d_1\)，即 \(r\) 是 \(S_{1...d_1}\) 的正周期，会发现 \(r,2r,3r,...,d_1-r,d_1\) 都是匹配位置。
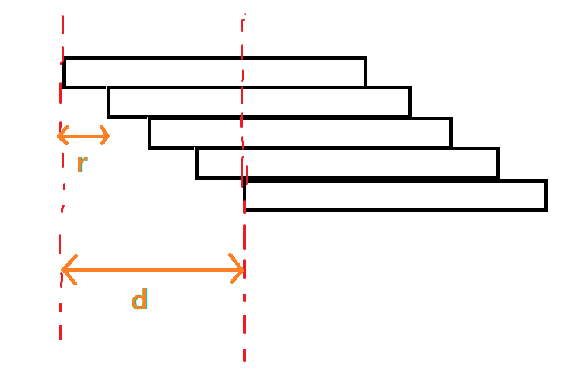
进一步可得这些匹配的位置是以 \(r\) 为公差的等差序列。
- \(\text{定理}(3)\)：对于一个字符串 \(S\)，\(S\) 的所有长度 \(\ge \dfrac {|S|}2\) 的 Border 的长度是一个等差序列。
证明：
考虑其中的两个长度 \(\ge \dfrac {|S|}2\) 的 Border，长度为 \(d_1,d_2\)，不妨设 \(d_1\) 为最大的 Border。
那么对应的，有周期 \(n-d_1,n-d_2\)。而 \(n-d_1+n-d_2\le n\)，根据弱周期引理有 \(r=\gcd(n-d_1,n-d_2)\) 也是周期。
因为 \(d_1\) 是最大的 Border，则有 \(r=n-d_1\)。
由于 \(r\) 是周期，则存在周期 \(r,2r,3r,...\)，以及存在对应的长度为 \(n-r,n-2r,n-3r,...\) 的 Border。
因此这些 Border 组成了公差为 \(r\) 的等差序列，证毕。
- \(\text{定理}(4)\)：一个字符串 \(S\) 的 Border 组成了 \(O(\log n)\) 个等差序列。
证明不会，直接拿结论用好了，这个用的比较广泛。
回文 Border 理论
- \(\text{定理}(1)\)：回文串的回文（前）后缀集合与其 Border 集合相同。
证明：
一个回文串 \(S\)，对于一个回文后缀 \(u\)，由于 \(S\) 的回文的，则 \(S\) 存在一个回文前缀 \(u\)。由于 \(u\) 是回文的，\(u=u_R\)，则 \(u\) 是 \(S\) 的前缀，进一步可知就是 Border。
对于一个 Border \(u\)，由 \(S\) 回文可知 \(u=u_R\)，即 \(u\) 是回文串。
证毕。
- \(\text{定理}(2)\)：对于字符串 \(S\) 的最长严格回文后缀 \(u\)，若 \(2|u|\ge |S|\)，那么 \(u\) 至多在 \(S\) 中出现两次：分别为前缀和后缀。
证明：考虑反证。
如果多出现了一次，起始位置为 \(p\)，那么有 \(1<p\le|u|\)。
那么 \(u_{p...|u|}\) 是 \(u\) 的一个 Border。根据 \(\text{定理}(1)\)，可知 \(u_{p...|u|}\) 是 \(u\) 的一个回文后缀，他是回文的。
而 \(u\) 也是回文的，因此 \((u_{1...p-1})_R=u_{|u|-p+1...|u|}\)，进而可知 \(u_{1...|u|+p-1}\) 也是回文的。而他又是 \(S\) 的一个前缀，且长度 \(>|u|\)，则他才是 \(S\) 的最长回文后缀，与 \(u\) 是最长回文后缀矛盾。
证毕。
结合普通 Border 论中的 \(\text{定理}(4)\) 和回文 Border 论中的 \(\text{定理}(2)\)，可以得到：一个回文串可以划分为若干个等差序列，并且每个序列内部满足相邻长度倍数 \(\le 2\)，显然个数为 \(O(\log n)\)。
回文划分 dp
考虑一个问题：一个由小写字母构成的字符串 \(S\)，求将 \(S\) 划分为若干个回文串的方案数。\(|S|\le 10^6\)
设 \(f[i]\) 表示以 \(i\) 结尾的方案数，转移：
我们把转移放到 PAM 上，可以枚举一条链上的点。
但还是 \(O(n^2)\)，我们考虑回文 Border 理论：字符串 \(S_{1...i}\) 的所有回文后缀可以划分成 \(O(\log n)\) 个等差序列。并且每个等差序列内部，前一个串在后一个串中作为前缀和后缀恰好出现两次。
设 \(g[x]\) 表示 PAM 上点 \(x\) 向上延伸的等差链对应的 dp 值的和。
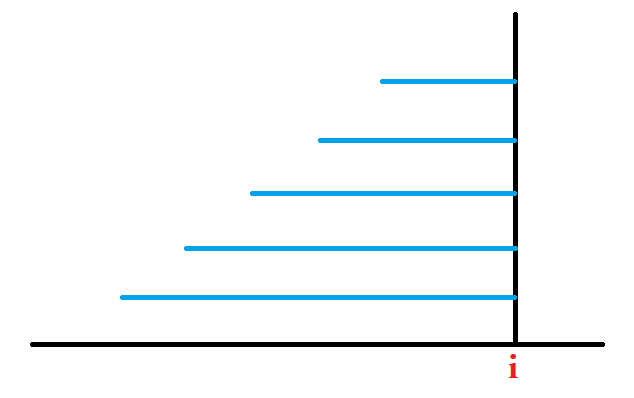
现在考虑一个等差序列，公差为 \(d\)，长这样：
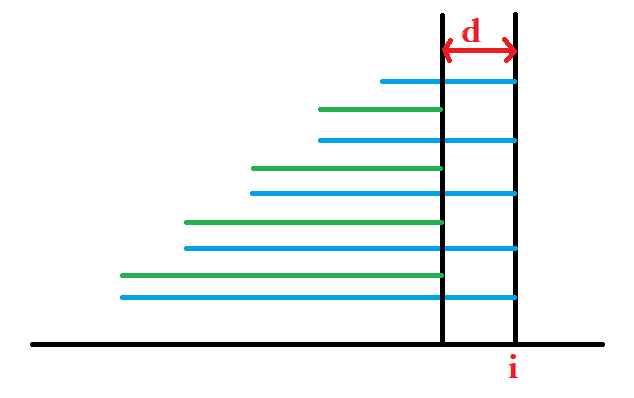
我们根据理论，很容易推出这些后缀上一次出现位置（除了最下面那个后缀）：
我们会发现除了最上面那个后缀，其他部分的贡献之前都在 \(f[i-d]\) 时算过。
每次取出链底 \(x\)，我们直接拿 \(g[fail(x)]\) 加上最上面那个后缀的贡献即可。
现在考虑正确性，我们可以证明上面的后缀上一次一定是对应的最长回文后缀：
反证，如果上面的后缀上一次出现时不是对应的最长后缀，因为他的长度的 \(2\) 倍 \(\ge\) 当前最长回文后缀的长度，所以往前接过去，当前回文后缀也会再次出现。而根据位置可知，当前回文后缀两次出现重叠，会出现一个更大的回文后缀，矛盾。
时间复杂度 \(O(n\log n)\)。
点击查看代码
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const ll maxn=1e6+10, mod=1e9+7;
struct node{
ll fail,len,ch[26],slk;
}a[maxn];
ll n,f[maxn],tot,las,dif[maxn],g[maxn];
char s[maxn];
ll ad(const ll &x,const ll &y) {return x+y>=mod? x+y-mod:x+y;}
void ins(ll i,ll c){
ll p=las;
while(s[i-a[p].len-1]-'a'!=c) p=a[p].fail;
if(!a[p].ch[c]){
ll np=las=++tot, q=a[p].fail;
while(s[i-a[q].len-1]-'a'!=c) q=a[q].fail;
if(!a[q].ch[c]) a[np].fail=2;
else a[np].fail=a[q].ch[c];
a[p].ch[c]=np, a[np].len=a[p].len+2;
dif[np]=a[np].len-a[a[np].fail].len;
a[np].slk=(dif[np]!=dif[a[np].fail]? a[np].fail:a[a[np].fail].slk);
} else las=a[p].ch[c];
}
int main()
{
scanf("%s",s+1); n=strlen(s+1);
tot=2, las=1;
a[1].fail=a[2].fail=1, a[1].len=-1;
f[0]=1;
for(ll i=1;i<=n;i++){
ins(i,s[i]-'a');
for(ll x=las;x>2;x=a[x].slk){
g[x]=f[i-a[a[x].slk].len-dif[x]];
if(a[x].slk!=a[x].fail) g[x]=ad(g[x],g[a[x].fail]);
f[i]=ad(f[i],g[x]);
}
}
printf("%lld",f[n]);
return 0;
}
例题
考虑把字符串改成 \(s_1s_ns_2s_{n-1}...\)，这样转为求划分为若干个偶回文串的方案数。
我们只在偶数的 \(i\) 处统计 \(f[i]\) 即可。记录
考虑可以离线怎么做。
\(r\) 从小到大扫描线，每个位置对应 PAM 上的一条链。
枚举链上的所有点，给 \(i-|u|+1\) 加上 \(1\)，每次查询就是求 \([l,n]\) 的总和。
考虑等差链划分，我们可以发现一条等差链很多贡献都会抵消，只需要求最上面长度和最下面的后缀上一次出现位置。
前者容易，后者考虑树上操作。每个 \(i\) 都对应一个点，然后链上所有点的出现时刻被刷新。考虑 dfn+线段树，单点修改，维护子树 max。
用主席树即可转为在线查询。记录
