cmd 的图论练习题
AGC010E Rearranging
题意:一个序列 \(a_{1...n}\),两个人游戏。先手打乱这个序列,然后后手可以多次选择一对相邻的互质的数交换。先手希望最终序列字典序尽量小,后手则相反。两人都绝顶聪明,求最终序列。
\(1\le n\le 2000,\space 1\le a_i\le 10^8\)
考虑不互质的两个数 \(a_i,a_j\),他们的相对顺序不会改变。可以发现,在确定所有数对的相对顺序情况下,后手可以任意操作。
在 \(i,j\) 之间连一条边,那么先手相当于给这些边定向成一个 DAG,然后后手给这个 DAG 找个字典序最大的拓扑序列。
因此现在要求的是:给一个图定向成 DAG,使得字典序最小的拓扑序最大。
可以先加一个超级源点,方便处理。
考虑 dfs。当前搜到了 \(u\),考虑所有连边,如果 \(v\) 没搜过则按 \(u\to v\) 的方向定向,否则 \(v\to u\)。我们先从大的点搜,如果可以连到小的话最好,否则也不亏。
最后一遍拓扑排序求最大字典序的拓扑序即可。记录
AGC038F Two Permutations
题意:两个 \(1\sim n\) 的排列 \(p_{1...n},q_{1...n}\),你需要确定另外两个排列 \(a,b\),满足 \(\forall i\in [1,n]\) 都有:
-
\(a_i=i\) 或 \(a_i=p_i\)
-
\(b_i=i\) 或 \(b_i=q_i\)
最大化 \(\sum\limits_{i=1}^n [a_i \not = b_i]\) 的个数,输出这个值。
\(1\le n\le 10^5\)
考虑求最小的 \(\sum\limits_{i=1}^n [a_i=b_i]\)。
对于 \(p\) 的每个环,对应的 \(a\) 要么全是 \(a_i=i\),要么全是 \(a_i=p_i\),\(q\) 同理。
那么相当于我们为 \(p\) 和 \(q\) 都选择若干个环,然后对于每个 \(i\) 分类讨论:
-
\(a_i=b_i=i\):此时贡献恒为 \(1\)
-
\(a_i\not=i,b_i=i\):当选择 \(p_i\) 所在环时贡献 \(1\)
-
\(a_i=i,b_i\not=i\):当选择 \(q_i\) 所在环时贡献 \(1\)
-
\(a_i\not=i,b_i\not=i,a_i\not=b_i\):当同时选择 \(p_i,q_i\) 所在环时贡献 \(1\)
-
\(a_i\not=i,b_i\not=i,a_i=b_i\):当同时选择或同时不选 \(p_i,q_i\) 所在环时贡献 \(1\)
考虑 \(p,q\) 环之间的“选、不选产生贡献”的问题,启发我们使用最小割。
(下面用 \(p,q\) 分别表示 \(p_i,q_i\) 所在环)考虑选择 \(p\) 则他与 \(S\) 连通,选择 \(q\) 则他与 \(T\) 连通。具体的:
-
\(a_i=b_i=i\):不用管
-
\(a_i\not=i,b_i=i\):连边 \(p\to T\)
-
\(a_i=i,b_i\not=i\):连边 \(S\to q\)
-
\(a_i\not=i,b_i\not=i,a_i\not=b_i\):连边 \(p\to q\)
-
\(a_i\not=i,b_i\not=i,a_i\not=b_i\):连边 \(p\to q\) 和 \(q\to p\)
时间复杂度 \(O(n\sqrt n)\)。
AGC008E Next or Nextnext
题意:给出 \(n,a_{1...n}\),其中 \(1\le a_i\le n\)。求有多少个 \(1\sim n\) 的排列 \(p\),满足对于 \(\forall i\in[1,n]\) 都有 \(a_i=p_i\) 或 \(a_i=p_{p_i}\)
\(1\le n\le 10^5\)
考虑连边 \(i\to a_i\),这是内向基环树森林,对于每个基环树分别求解。
先找出当前环。我们要构造 \(p\),环上点一定是错杂的排列在 \(p\) 的环上。
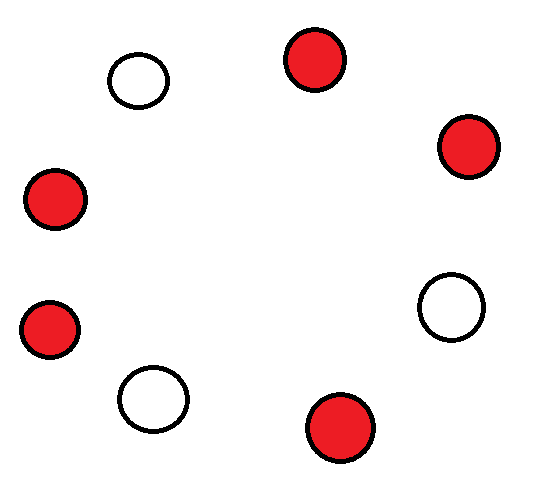
(红色是基环树的环上点)
不难发现,如果一个环上点与非环上点的连边数量 \(>1\),一定无解。
进一步的,如果存在一个点(可以不在环上),他和非环上点的连边数量 \(>1\),无解。
考虑判完之后基环树长这样:
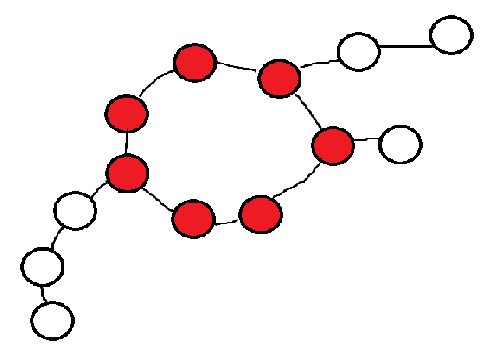
即每个环上点都可能带着一条链。
考虑一点环上点带着一个环外点,这个环外点可以塞进该环上点和前一个环上点的缝隙中。如果前一个点没有带着链,还可以塞入前一个的缝隙。
如果带着一条 \(s\) 个的链,考虑前面有 \(r\) 个缝隙:
-
\(s>r\):无解
-
\(s=r\):方案数为 \(1\)
-
\(s>r\):方案数为 \(2\)
这样就可以做了。
但是还要判断所有点都不带链的情况,稍微手玩一下会发现一个大小为 \(S\) 的环可以合并成大小为 \(2S\) 的环,方案数为 \(S\)。
一个长度 \(S\) 大于 \(1\) 的奇环可以让每个点都往后跳两步,操作后还是一个环,方案数为 \(2\)。
把单独的环分出来,按大小分类,枚举多少个环合并,随便乘一下。
时间 \(O(n)\)。记录
Luogu7054 Graph
题意:一张 \(n\) 个点、\(m\) 条有向边的 DAG,你可以加入至多 \(k\) 条有向边,满足加边后仍然是 DAG,使得最小的拓扑序尽量大。输出拓扑序以及加边方案。
\(1\le n,m\le 10^5\)
考虑拓扑序中第一个数,对于所有入度为零的点,我们会选择呢编号尽量大的,然后那个点向比他小的零入度点连有向边,之后继续做。
但这样是错误的。具体的,如果我们加入边 \(x\to y,x\to z,y\to z\),那么 \(x\to z\) 是没用的。
当前局面下,考虑有多少个 “已经加过入边” 的点 和 多少个 “还没加过入边” 的点。我们确定当前取出得点 \(u\) 时,对于 “已经加过入边” 的编号 \(<u\) 的点,我们其实是不需要加边的,只需让他的入边起点变成 \(u\);对于 “还没加过入边” 的点,我们才需要额外加边。
大致思路就是这样。考虑具体实现,我们需要把两类点分开,用大根堆 \(q_1\) 和小根堆 \(q_2\) 分别存储两类点。
每次判断剩余的 \(k\) 与 \(|q_2|\) 的大小关系来确定取出的点 \(u\):
-
\(k<|q_2|\):此时 \(u\) 为 \(q_2\) 中第 \(k+1\) 小的点。然后需要把 \(u\) 向前 \(1...k\) 小的点分别连边,即把这些点移到 \(q_1\)
-
\(k\ge |q_2|\):先把 \(q_2\) 中除了最大值,其他全部移到 \(q_1\)。再判断 \(q_1\) 最大值和 \(q_2\) 剩下一个点编号的大小,如果 \(q_2\) 大则 \(u\) 为 \(q_2\) 剩下的点,如果 \(q_1\) 最大值大则继续把 \(q_2\) 剩下一个点移到 \(q_1\),取 \(u\) 为 \(q_1\) 最大值,并更新 \(k\)。
出现一个零入度点 \(v\) 时,把 \(v\) 加入 \(q_2\)。
时间复杂度 \(O(n\log n+m)\)。记录
AGC016E Poor Turkeys
题意:有 \(n\) 个物品和 \(m\) 次操作,第 \(i\) 次给出 \(x_i,y_i\) 表示:
-
若第 \(x_i,y_i\) 个物品都存在,则随便选其中一个取走
-
若 \(x_i,y_i\) 恰好一个存在,则取走那一个
-
若都不存在,什么都不做
求有多少个无序二元组 \((i,j)\) 满足存在一种操作方案使得最终物品 \(i,j\) 都存在。
\(1\le n\le 400,\space 1\le m\le 10^5\)
考虑对于单个 \(i\),求最终物品 \(i\) 是否可能存在。
我们考虑“染色”,一开始把 \(i\) 染成白色,其他是黑色。
考虑倒着来扫描每个操作,如果当前操作的两个点中恰好一个是白色,把另一个染白;如果两个都是白色,无解;如果都是黑色,什么都不做。
一对 \((i,j)\) 合法的必要条件是 \(i,j\) 分别都有解。通过上面的过程,可知每个点都对应一棵该点为根的生成树。
现在考虑按照时间顺序合并这两棵生成树,根据 \(i,j\) 为根时每个点的染色时间来归并每次的染色。
然后我们会发现,比如一个点 \(x\) 在 \(i,j\) 为根的生成树中都染了色,时间为 \(p,q(p<q)\),那么 \(x\) 会在时刻 \(p\) 时染色。在时刻 \(q\) 时,由于他在 \(j\) 为根的生成树中的前驱已是白色,而他在之前时刻 \(p\) 时就已经染了白色,因此对于时刻 \(q\) 的这个操作,两个点都是白色,无解。
因此,\((i,j)\) 合法的充要条件是 \(i,j\) 这两棵生成树无交集。
因为数据范围很小,随便做就行,时间 \(O(n(m+n^2))\)。记录

