近期总结 2024.2.7

AGC035E Develop

题意：现在有 \(1,2,3,...,n\) 共 \(n\) 个数字，每次删去一个已有的数字 \(x\)，然后：若 \(x-2\) 不存在，且 \(x-2\in [1,n]\)，则重新加入 \(x-2\)；若 \(x+k\) 不存在，且 \(x+k\in [1,n]\)，则重新加入 \(x+k\)。问经过若干次删除后剩余数字集合有多少种可能，答案模 \(m\)。\(1\le k\le n\le 150,\space 10^8\le m\le 10^9\)

---

注意到只有唯一一种删除一个数的方法，当删除 \(x\) 时，如果 \(x-2,x+k\) 合法且已删去，我们就得加回来，这样一来先前删去 \(x-2\) 或 \(x+k\) 的操作是没有用的。

因此，我们必须保证删数过程中不能有数被加回来。

把 \(x\) 向 \(x-2,x+k\) 连边，相当于我们选 \(n\) 个点中的若干个点，这些点不构成环。

当 \(k\) 为偶数时，奇偶数字对应的点之间没有连边，奇偶可以分开算，此时相当于一排点中选若干个点，不存在连续 \(\frac k2\) 个点被选择，可以直接 dp 解决。

当 \(k\) 为奇数时，整张图如下

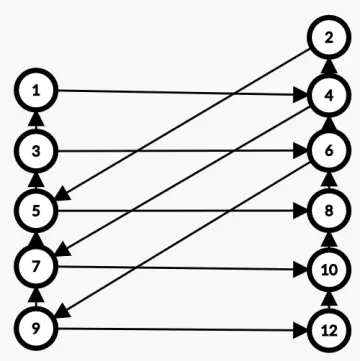
如图，注意到环上点的个数都是 \(k+2\)。

考虑一层一层来 dp。

设 \(f[i,j,x]\) 表示考虑了前 \(i\) 层，从右边往下走，然后在左边走一段，形如这样已走到左边第 \(i\) 层的路径最长长度为 \(j\)，右边已经连续选了 \(x\) 个点。

转移考虑左右边是否有点，分类讨论四种情况，然后用 \(x\) 去 chkmax \(j\) 即可。时间复杂度 \(O(n^3)\)。

---

CF627E Orchestra

题意：一个大小为 \(r\times c\) 的网格，有 \(n\) 个格子被染黑，求有多少个连续子矩阵至少包含 \(k\) 个黑格。

\(1\le r,c,n\le 3\times 10^3,\space 1\le k\le 10\)

---

枚举子矩阵的左上角坐标，考虑用类似于单调栈的东西维护右下角。

发现加入一个点时，单调栈的每个位置都要变化，难以维护。

考虑枚举子矩阵的上下边界。

设 \(p_i\) 表示左边界为第 \(i\) 列时，右边界的选择方案数。

当有点加入时，我们动态维护这些点的列的有序多重集，每连续 \(k\) 个点都会产生一次贡献。

用 multiset 维护多重集，每次支持快速查询一个数的前驱后继，暴力地查询新加入地数的前面 \(k\) 个数和后面 \(k\) 个数，更新贡献，时间复杂度 \(O(r(r+nk\log n))\)，无法通过。

考虑一个经典的操作，把从后往前枚举下边界，把加点改成删点，用链表维护，这和秃子酋长一题是类似的。

如此一来，时间复杂度 \(O(r(r+nk))\)。

---

CF1067D Computer Game

题意：有 \(n\) 个游戏，每个游戏有收益 \(a_i\)，升级后的收益 \(b_i\)，每次成功概率 \(p_i\)。每秒可以玩一个游戏，如果成功则得到当前收益，并且可以升级任意某个游戏。求 \(t\) 秒后的期望收益的最大值。\(n\le 10^5,\space t\le 10^{10},\space a_i<b_i\)

---

当我们玩一个游戏成功时，一定会解锁 \(b_i\cdot p_i\) 最大的游戏，然后剩下的时间就会一直玩这个游戏。

但是一开始我们应该玩哪个游戏？是成功概率高的还是期望收益大的呢？

设 \(f[i]\) 表示剩余 \(i\) 时间时的最大期望收益总和，设 \(M\) 为 \(b_i\cdot p_i\) 的最大值。

\[\begin{aligned} f[i] &= \max_{j}\{p_j(a_j+M(i-1))+(1-p_j)f[i-1]\} \\ &= f[i-1]+\max_{j}\{p_j(a_j+M(i-1)-f[i-1])\} \\ &= f[i-1]+\max_j\{p_ja_j-p_j(f[i-1]-M(i-1))\} \end{aligned} \]

对于 \(j\in[1,n]\)，对应一个点 \((p_j,p_ja_j)\) 在平面上，那么相当于我们用一条斜率为 \(f[i-1]-M(i-1)\) 的线去切这些点，所得到的截距最大值。先求出 \(n\) 个点的上凸包，然后用一条斜率为 \(f[i-1]-M(i-1)\) 去切这个凸包。

注意到 \(f[i-1]-M(i-1)\) 一定是在不断变小的，那么我们切到的点是从前往后有序的，即 \(i\in[1,t]\) 选择的决策是有序成段的。

枚举每个点，算出有多少个 \(i\in[1,t]\) 会切到这个点。考虑二分，然后求出对应斜率，与当前点和下一个点的斜率比较。

设我们已经处理了 \(f[1...x]\)，我们二分选择这个决策的状态个数，对于一个相应的 \(i\)，设决策为 \(j\)，不难得到

\[f[i]=p_j(a_j+M(i-1))+(1-p_j)f[i-1] \]

二分到的 \(mid\) 会很大，考虑矩阵优化这样的转移。

\[\begin{bmatrix} f[i-1] & i-1 & 1 \end{bmatrix} \times \begin{bmatrix} 1-p_j & 0 & 0 \\ M\cdot p_j & 1 & 0\\ p_j\cdot a_j & 1 & 1 \end{bmatrix} = \begin{bmatrix} f[i] & i & 1 \end{bmatrix} \]

这样是两只 \(\log\)，带 \(27\) 的常数，无法通过。

考虑一个经典的优化，预处理 \(2\) 的幂指数的矩阵幂，然后改二分为倍增。

这样时间复杂度为 \(O(n\log t)\)。