一种神奇的平衡树——WBLT

参考文献

王思齐《Leafy Tree 及其实现的加权平衡树》

WBLT 是一种神奇的平衡树，全名 Weight Balanced Leafy Tree。

lxl 在冬令营上简单地提及了这个东西，这个东西非常好用，当然的确非常好用。

下面我们来介绍这个东西。

Leafy Tree#

Leafy Tree，顾名思义，是一类只有叶子结点存储信息的数据结构，一个常见的例子是线段树。

用 Leafy Tree 维护 BST，其实跟线段树的写法是类似的。先抛开平衡，以普通平衡树为例，我们逐一介绍维护方法。

基本性质

先了解一下基本的性质。

每个点要么有两个儿子，要么没有儿子，显然对于 Leafy Tree 来说只有一个儿子的点没什么用。

每个点（包括非叶子）需要存储一个权值 $v a l$ ，如果是叶子存的就是键值，否则存的是子树内叶子的权值最大值。

由于子树内叶子的权值是中序遍历单调不降的，一个非叶点的权值是右儿子的权值。

每个点也可以同时维护子树内的叶子大小，这和其他平衡树是类似的。

下面一部分代码中的 maintain 是维护平衡，读者可以先忽略。

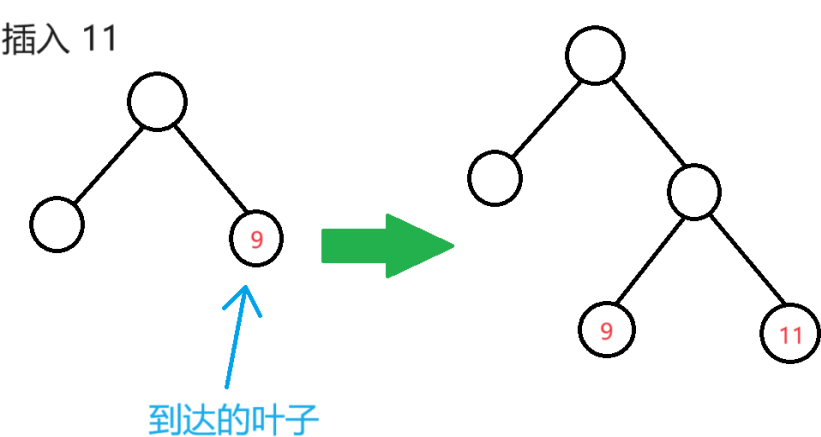
插入一个元素 ins

从根开始，逐一比较插入的值和左子树的权值，这和线段树上二分是类似的。

当我们到达叶子时，我们需要将插入的值和叶子合并。

一个显然的想法是，新建两个点，一个是表示插入的值的叶子，一个是这两个叶子的父节点。

下图是一个例子。

点击查看代码

void ins(ll p,ll v){
	if(isleaf(p)){
		ls(p)=Newnode(min(v,a[p].val));
		rs(p)=Newnode(max(v,a[p].val));
		pushup(p); return;
	}
	if(v<=a[ls(p)].val) ins(ls(p),v);
	else ins(rs(p),v);
	pushup(p); maintain(p);
}

删除一个元素 del

依然从根开始，走到对应的叶子，此时我们需要删掉这个叶子。

但是直接删会破坏性质（每个点要么两个儿子，要么没有儿子），需要把该叶子的兄弟搬到父亲上来。

只需要在递归的同时记录一下父亲即可。

点击查看代码

void del(ll p,ll v,ll fa){
	if(isleaf(p)){
		if(ls(fa)==p) a[fa]=a[rs(fa)];
		else a[fa]=a[ls(fa)];
		return;
	}
	if(v<=a[ls(p)].val) del(ls(p),v,p);
	else del(rs(p),v,p);
	if(!isleaf(p)) pushup(p);
	maintain(p);
}

维护平衡#

显然 Leafy Tree 可以被卡成平方。

因此引入 Weight Balanced Leafy Tree，来保持平衡。

具体的，WBLT 和许多平衡树一样，依靠旋转来保持平衡。

我们定义平衡因子 $α$ ，表示定义对于一个非叶点 $p$ ，当且仅当 $min (s i z [l s (p)], s i z [r s (p)]) \geq α \cdot s i z [p]$ 时点 $p$ 平衡。

为了维护平衡，WBLT 使用了单旋和双旋两种方式。

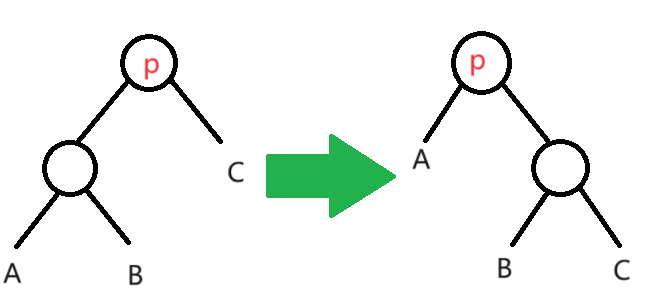
单旋

对于一个不平衡的点 $p$ ，不妨设 $s i z [l s (p)] > s i z [r s (p)]$ ，此时我们把 $l s (p)$ 旋转上来。

不难发现 $l s (p)$ 一定不是叶子，那么 $l s (p)$ 本质上是不存储信息的，为了不改变指针，我们可以直接把 $l s (p)$ 旋到 $p$ 的右儿子。

具体的：

但是旋转之后真的能保持平衡吗？考虑计算 $p$ 和旋转后 $r s (p)$ 能平衡的条件。

太麻烦了，略。

双旋

单旋对于 WBLT 来说是错误的，正确的解法是双旋。

具体的，假设我们要旋转 $l s (p)$ ，我们需要先判断 $l s (p)$ 的右边是否过重，否则旋转之后可能仍然不平衡。

具体的做法是，判断 $s i z [r s (l s (p))] > \frac{1 - 2 α}{1 - α} s i z [l s (p)]$ ，若满足条件则把 $l s (p)$ 的右儿子旋转。

证明见 oi-wiki。~~（直接背就行~~

一般取 $α = 0.25$ 。

点击查看代码

void rot(ll p,ll d){
	if(d==0){
		ll tmp=ls(p);
		ls(p)=ls(ls(p));
		ls(tmp)=rs(tmp);
		rs(tmp)=rs(p);
		rs(p)=tmp; pushup(tmp);
	} else{
		ll tmp=rs(p);
		rs(p)=rs(rs(p));
		rs(tmp)=ls(tmp);
		ls(tmp)=ls(p);
		ls(p)=tmp; pushup(tmp);
	} pushup(p);
}
void maintain(ll p){
	if(a[ls(p)].siz>a[rs(p)].siz*3){
		if(a[rs(ls(p))].siz>a[ls(ls(p))].siz*2){
			rot(ls(p),1);
		} rot(p,0);
	} else if(a[rs(p)].siz>a[ls(p)].siz*3){
		if(a[ls(rs(p))].siz>a[rs(rs(p))].siz*2){
			rot(rs(p),0);
		} rot(p,1);
	}
}

然后其他操作就直接略了。

下面是普通平衡树的代码。

点击查看代码

#include<bits/stdc++.h>
#define ls(p) a[p].lc
#define rs(p) a[p].rc
#define ll long long
using namespace std;
const ll maxn=2e5+10;
ll n,op,x,tot,rt;
struct node{
	ll lc,rc,val,siz;
}a[maxn];
ll Newnode(ll v){
	++tot;
	a[tot].val=v, a[tot].siz=1;
	return tot;
}
bool isleaf(ll p){
	return !ls(p)||!rs(p);
}
void pushup(ll p){
	a[p].siz=a[ls(p)].siz+a[rs(p)].siz;
	a[p].val=a[rs(p)].val;
}
void rot(ll p,ll d){
	if(d==0){
		ll tmp=ls(p);
		ls(p)=ls(ls(p));
		ls(tmp)=rs(tmp);
		rs(tmp)=rs(p);
		rs(p)=tmp; pushup(tmp);
	} else{
		ll tmp=rs(p);
		rs(p)=rs(rs(p));
		rs(tmp)=ls(tmp);
		ls(tmp)=ls(p);
		ls(p)=tmp; pushup(tmp);
	} pushup(p);
}
void maintain(ll p){
	if(a[ls(p)].siz>a[rs(p)].siz*3){
		if(a[rs(ls(p))].siz>a[ls(ls(p))].siz*2){
			rot(ls(p),1);
		} rot(p,0);
	} else if(a[rs(p)].siz>a[ls(p)].siz*3){
		if(a[ls(rs(p))].siz>a[rs(rs(p))].siz*2){
			rot(rs(p),0);
		} rot(p,1);
	}
}
void ins(ll p,ll v){
	if(isleaf(p)){
		ls(p)=Newnode(min(v,a[p].val));
		rs(p)=Newnode(max(v,a[p].val));
		pushup(p); return;
	}
	if(v<=a[ls(p)].val) ins(ls(p),v);
	else ins(rs(p),v);
	pushup(p); maintain(p);
}
void del(ll p,ll v,ll fa){
	if(isleaf(p)){
		if(ls(fa)==p) a[fa]=a[rs(fa)];
		else a[fa]=a[ls(fa)];
		return;
	}
	if(v<=a[ls(p)].val) del(ls(p),v,p);
	else del(rs(p),v,p);
	if(!isleaf(p)) pushup(p);
	maintain(p);
}
ll Count(ll p,ll v){
	if(isleaf(p)) return a[p].val<=v;
	if(a[ls(p)].val>v) return Count(ls(p),v);
	return Count(rs(p),v)+a[ls(p)].siz;
}
ll find(ll p,ll k){
	if(a[p].siz==k) return a[p].val;
	if(a[ls(p)].siz>=k) return find(ls(p),k);
	else return find(rs(p),k-a[ls(p)].siz);
}
int main(){
	rt=Newnode(1e17);
	scanf("%lld",&n);
	while(n--){
		scanf("%lld%lld",&op,&x);
		if(op==1) ins(rt,x);
		else if(op==2) del(rt,x,0);
		else if(op==3) printf("%lld\n",Count(rt,x-1)+1);
		else if(op==4) printf("%lld\n",find(rt,x));
		else if(op==5) printf("%lld\n",find(rt,Count(rt,x-1)));
		else printf("%lld\n",find(rt,Count(rt,x)+1));
	}
	return 0;
}

和 splay 对比一下。

测试点编号	Splay	WBLT
1	$3 m s$	$3 m s$
2	$3 m s$	$3 m s$
3	$3 m s$	$3 m s$
4	$3 m s$	$3 m s$
5	$4 m s$	$3 m s$
6	$10 m s$	$3 m s$
7	$45 m s$	$4 m s$
8	$3 m s$	$6 m s$
9	$94 m s$	$21 m s$
10	$94 m s$	$44 m s$

不难发现 WBLT 还挺快。

更常规的操作#

合并

合并两棵 WBLT，不妨设根为 $p, q$ 。

钦定 $s i z [p] \geq s i z [q]$

根据论文，进行分类讨论：

若 $s i z [q] \geq α (s i z [p] + s i z [q])$ ，直接新建一个点，为 $p, q$ 的父节点即可。

否则，若 $s i z [l s (p)] \geq α (s i z [p] + s i z [q])$ ，递归合并 $r s (p)$ 和 $q$ ，然后和 $l s (p)$ 合并。

否则，分别递归合并 $l s (p), l s (r s (p))$ ，以及 $r s (r s (p)), q$ ，最后把两个合并。

点击查看代码

ll merge(ll p,ll q){
	if(!p||!q) return p|q;
	if(4*min(a[p].siz,a[q].siz)>=(a[p].siz+a[q].siz)){
		ll x=Newnode(0);
		ls(x)=p, rs(x)=q;
		pushup(x); return x;
	}
	if(a[p].siz>=a[q].siz){
		if(4*a[ls(p)].siz>=a[p].siz+a[q].siz) return merge(ls(p),merge(rs(p),q));
		else return merge(merge(ls(p),ls(rs(p))),merge(rs(rs(p)),q));
	} else{
		if(4*a[rs(q)].siz>=a[p].siz+a[q].siz) return merge(merge(p,ls(q)),rs(q));
		else return merge(merge(p,ls(ls(q))),merge(rs(ls(q)),rs(q)));
	}
}

分裂

类似于线段树，先走到叶子。

然后逐一将分裂的一边的所有子树合并。

分裂的时间复杂度都是 $O (\log n)$ 的，而合并是 $O (\log \frac{m a x s i z e}{m i n s i z e})$

但是常数有一点大，注意分裂后走过的路径上的点都会废掉，一定要垃圾回收，否则空间容易爆炸。

点击查看代码

void split(ll p,ll k,ll &x,ll &y){
	if(isleaf(p)){
		if(k==0) y=p, x=0;
		else x=p, y=0;
		return;
	}
	if(a[ls(p)].siz>=k){
		split(ls(p),k,x,y);
		y=merge(y,rs(p));
	} else{
		split(rs(p),k-a[ls(p)].siz,x,y);
		x=merge(ls(p),x);
	} trs[++len]=p;
}

有了分裂与合并，WBLT 也能支持区间翻转。

点击查看代码

#include<bits/stdc++.h>
#define ls(p) a[p].lc
#define rs(p) a[p].rc
#define ll int
using namespace std;
const ll maxn=1e7+10;
ll n,m,l,r,tot,rt,trs[maxn],len;
struct node{
	ll lc,rc,val,siz,rev;
}a[maxn];
ll Newnode(ll v){
	ll p=(len? trs[len--]:++tot);
	a[p].val=v, a[p].siz=1;
	ls(p)=rs(p)=a[p].rev=0;
	return p;
}
bool isleaf(ll p){
	return !ls(p)||!rs(p);
}
void pushup(ll p){
	a[p].siz=a[ls(p)].siz+a[rs(p)].siz;
	a[p].val=a[rs(p)].val;
}
void pushdown(ll p){
	if(!a[p].rev) return;
	a[p].rev=0;
	swap(ls(p),rs(p));
	a[ls(p)].rev^=1, a[rs(p)].rev^=1;
}
void rot(ll p,ll d){
	if(d==0){
		ll tmp=ls(p);
		ls(p)=ls(ls(p));
		ls(tmp)=rs(tmp);
		rs(tmp)=rs(p);
		rs(p)=tmp; pushup(tmp);
	} else{
		ll tmp=rs(p);
		rs(p)=rs(rs(p));
		rs(tmp)=ls(tmp);
		ls(tmp)=ls(p);
		ls(p)=tmp; pushup(tmp);
	} pushup(p);
}
void maintain(ll p){
	if(a[ls(p)].siz>a[rs(p)].siz*3){
		if(a[rs(ls(p))].siz>a[ls(ls(p))].siz*2){
			rot(ls(p),1);
		} rot(p,0);
	} else if(a[rs(p)].siz>a[ls(p)].siz*3){
		if(a[ls(rs(p))].siz>a[rs(rs(p))].siz*2){
			rot(rs(p),0);
		} rot(p,1);
	}
}
ll build(ll l,ll r){
	if(l==r){
		return Newnode(l);
	} ll mid=l+r>>1;
	ll p=++tot;
	ls(p)=build(l,mid), rs(p)=build(mid+1,r);
	pushup(p); return p;
}
ll merge(ll p,ll q){
	if(!p||!q) return p|q;
	if(4*min(a[p].siz,a[q].siz)>=(a[p].siz+a[q].siz)){
		ll x=Newnode(0);
		ls(x)=p, rs(x)=q;
		pushup(x); return x;
	}
	if(a[p].siz>=a[q].siz){
		pushdown(p);
		if(4*a[ls(p)].siz>=a[p].siz+a[q].siz) return merge(ls(p),merge(rs(p),q));
		else{
			pushdown(rs(p));
			return merge(merge(ls(p),ls(rs(p))),merge(rs(rs(p)),q));
		}
	} else{
		pushdown(q);
		if(4*a[rs(q)].siz>=a[p].siz+a[q].siz) return merge(merge(p,ls(q)),rs(q));
		else{
			pushdown(ls(q));
			return merge(merge(p,ls(ls(q))),merge(rs(ls(q)),rs(q)));
		}
	}
}
void split(ll p,ll k,ll &x,ll &y){
	if(isleaf(p)){
		if(k==0) y=p, x=0;
		else x=p, y=0;
		return;
	}
	pushdown(p);
	if(a[ls(p)].siz>=k){
		split(ls(p),k,x,y);
		y=merge(y,rs(p));
	} else{
		split(rs(p),k-a[ls(p)].siz,x,y);
		x=merge(ls(p),x);
	} trs[++len]=p;
}
void dfs(ll p){
	if(isleaf(p)){
		printf("%d ",a[p].val); return;
	}
	pushdown(p);
	dfs(ls(p));
	dfs(rs(p));
}
ll s1,s2,s3;
int main(){
	scanf("%d%d",&n,&m);
	rt=build(1,n);
	for(ll i=1;i<=m;i++){
		scanf("%d%d",&l,&r);
		split(rt,r,s1,s3);
		split(s1,l-1,s1,s2);
		a[s2].rev^=1;
		rt=merge(merge(s1,s2),s3);
	}
	dfs(rt);
	return 0;
}

与 Splay 和 fhq-treap 的比较（根据文艺平衡树）

测试点	Splay	fhq-treap	WBLT
1	$4 m s$	$4 m s$	$3 m s$
2	$4 m s$	$4 m s$	$4 m s$
3	$13 m s$	$14 m s$	$17 m s$
4	$147 m s$	$188 m s$	$207 m s$
5	$151 m s$	$185 m s$	$202 m s$
6	$102 m s$	$91 m s$	$156 m s$

结果 WBLT 成了最慢的，惊奇的是 Splay 反倒成了最快的。

可知在只有区间翻转的时候，Splay 比较占优势。

或者说，分裂和合并的常数比较大？而且 Splay 不需要分裂和合并。

持久化操作#

当然 WBLT 也支持持久化。

在插入和删除时，和其他数据结构类似，WBLT 也是采用路径复制的方法。

在旋转 $l s (p)$ 的时候，不难发现只有插入和删除会触发旋转，因此 $p$ 是在插入或删除的时候已经通过路径复制新建的点，我们不需要对 $p$ 额外复制。

但是， $l s (p)$ 可能不是路径复制上的点，我们需要对 $l s (p)$ 复制。

模板题

点击查看代码

#include<bits/stdc++.h>
#define ls(p) a[p].lc
#define rs(p) a[p].rc
#define ll long long
using namespace std;
const ll maxn=1e7+10;
ll n,t,op,x,tot,rt[maxn],c;
struct node{
	ll lc,rc,val,siz;
}a[maxn];
ll Newnode(ll v){
	++tot;
	a[tot].val=v, a[tot].siz=1;
	return tot;
}
bool isleaf(ll p){
	return !ls(p)||!rs(p);
}
void pushup(ll p){
	a[p].siz=a[ls(p)].siz+a[rs(p)].siz;
	a[p].val=a[rs(p)].val;
}
void rot(ll p,ll d){
	if(d==0){
		a[++tot]=a[ls(p)], ls(p)=tot;
		ll tmp=ls(p);
		ls(p)=ls(ls(p));
		ls(tmp)=rs(tmp);
		rs(tmp)=rs(p);
		rs(p)=tmp; pushup(tmp);
	} else{
		a[++tot]=a[rs(p)], rs(p)=tot;
		ll tmp=rs(p);
		rs(p)=rs(rs(p));
		rs(tmp)=ls(tmp);
		ls(tmp)=ls(p);
		ls(p)=tmp; pushup(tmp);
	} pushup(p);
}
void maintain(ll p){
	if(a[ls(p)].siz>a[rs(p)].siz*3){
		if(a[rs(ls(p))].siz>a[ls(ls(p))].siz*2){
			rot(ls(p),1);
		}
		rot(p,0);
	} else if(a[rs(p)].siz>a[ls(p)].siz*3){
		if(a[ls(rs(p))].siz>a[rs(rs(p))].siz*2){
			rot(rs(p),0);
		}
		rot(p,1);
	}
}
void ins(ll &p,ll v){
	a[++tot]=a[p]; p=tot;
	if(isleaf(p)){
		ls(p)=Newnode(min(v,a[p].val));
		rs(p)=Newnode(max(v,a[p].val));
		pushup(p); return;
	}
	if(v<=a[ls(p)].val) ins(ls(p),v);
	else ins(rs(p),v);
	pushup(p); maintain(p);
}
void del(ll &p,ll v,ll fa){
	if(isleaf(p)){
		if(a[p].val!=v) return;
		if(ls(fa)==p) a[fa]=a[rs(fa)];
		else a[fa]=a[ls(fa)];
		return;
	}
	a[++tot]=a[p]; p=tot;
	if(v<=a[ls(p)].val) del(ls(p),v,p);
	else del(rs(p),v,p);
	if(!isleaf(p)) pushup(p);
	maintain(p);
}
ll Count(ll p,ll v){
	if(isleaf(p)) return a[p].val<=v;
	if(a[ls(p)].val>v) return Count(ls(p),v);
	return Count(rs(p),v)+a[ls(p)].siz;
}
ll find(ll p,ll k){
	if(a[p].siz==k) return a[p].val;
	if(a[ls(p)].siz>=k) return find(ls(p),k);
	else return find(rs(p),k-a[ls(p)].siz);
}
int main(){
	rt[0]=tot=1;
	ls(rt[0])=Newnode(-0x7fffffff), rs(rt[0])=Newnode(0x7fffffff);
	pushup(rt[0]);
	scanf("%lld",&n);
	for(ll i=1;i<=n;i++){
		scanf("%lld%lld%lld",&t,&op,&x);
		rt[i]=rt[t];
		if(op==1) ins(rt[i],x), ++c;
		else if(op==2) del(rt[i],x,0), --c;
		else if(op==3) printf("%lld\n",Count(rt[i],x-1));
		else if(op==4) printf("%lld\n",find(rt[i],x+1));
		else if(op==5) printf("%lld\n",find(rt[i],Count(rt[i],x-1)));
		else printf("%lld\n",find(rt[i],Count(rt[i],x)+1));
	}
	return 0;
}

分裂与合并的持久化

考虑合并的持久化。

观察合并的代码，不难发现合并的过程中并没有破坏原来树的结构，实际上普通的合并已经满足可持久化了。

分裂同理，也满足。

模板题中同时存在插入和翻转操作，注意叶子标记的处理。

点击查看代码

#include<bits/stdc++.h>
#define ls(p) a[p].lc
#define rs(p) a[p].rc
#define ll long long
using namespace std;
const ll maxn=2e7+10;
ll n,t,op,x,y,tot,c,s1,s2,s3;
int rt[200010];
struct node{
	int siz,lc,rc,rev;
	ll sum;
}a[maxn];
ll Newnode(ll v){
	++tot;
	a[tot].siz=1, a[tot].sum=v;
	return tot;
}
bool isleaf(ll p){
	return !ls(p)||!rs(p); 
}
void pushup(ll p){
	a[p].sum=a[ls(p)].sum+a[rs(p)].sum;
	a[p].siz=a[ls(p)].siz+a[rs(p)].siz;
}
void pushdown(ll p){
	if(isleaf(p)||!a[p].rev) return;
	a[p].rev=0;
	if(!isleaf(ls(p))) a[++tot]=a[ls(p)], ls(p)=tot;
	if(!isleaf(rs(p))) a[++tot]=a[rs(p)], rs(p)=tot;
	a[ls(p)].rev^=1, a[rs(p)].rev^=1;
	swap(ls(p),rs(p));
}
void rot(ll p,ll d){
	if(d==0){
		ll tmp=++tot; a[tmp]=a[ls(p)];
		ls(p)=ls(tmp);
		ls(tmp)=rs(tmp), rs(tmp)=rs(p);
		rs(p)=tmp; pushup(tmp);
	} else{
		ll tmp=++tot; a[tmp]=a[rs(p)];
		rs(p)=rs(tmp);
		rs(tmp)=ls(tmp), ls(tmp)=ls(p);
		ls(p)=tmp; pushup(tmp);
	} pushup(p);
}
void maintain(ll p){
	pushdown(p);
	if(a[rs(p)].siz*3<a[ls(p)].siz){
		pushdown(ls(p));
		if(a[ls(ls(p))].siz*2<a[rs(ls(p))].siz){
			pushdown(rs(ls(p))); rot(ls(p),1);
		} rot(p,0);
	} else if(a[ls(p)].siz*3<a[rs(p)].siz){
		pushdown(rs(p));
		if(a[rs(rs(p))].siz*2<a[ls(rs(p))].siz){
			pushdown(ls(rs(p))); rot(rs(p),0);
		} rot(p,1);
	}
}
void ins(int &p,ll k,ll v){
	a[++tot]=a[p], p=tot;
	if(isleaf(p)){
		ls(p)=Newnode(k==0? v:a[p].sum), rs(p)=Newnode(k==1? v:a[p].sum);
		a[p].rev=0; //注意叶子标记问题！！！  
		pushup(p); return;
	} pushdown(p);
	if(k<=a[ls(p)].siz) ins(ls(p),k,v);
	else ins(rs(p),k-a[ls(p)].siz,v);
	pushup(p); maintain(p);
}
void del(int &p,ll k){
	a[++tot]=a[p], p=tot;
	pushdown(p);
	if(k<=a[ls(p)].siz){
		if(isleaf(ls(p))) a[p]=a[rs(p)];
		else{
			del(ls(p),k);
			pushup(p); maintain(p);
		}
	} else{
		if(isleaf(rs(p))) a[p]=a[ls(p)];
		else {
			del(rs(p),k-a[ls(p)].siz);
			pushup(p); maintain(p);
		}
	}
}
ll merge(ll p,ll q){
	if(!p||!q) return p|q;
	if(4*min(a[p].siz,a[q].siz)>=a[p].siz+a[q].siz){
		ll r=++tot; ls(r)=p, rs(r)=q;
		pushup(r); return r;
	}
	if(a[p].siz>=a[q].siz){
		pushdown(p);
		if(4*a[ls(p)].siz>=a[p].siz+a[q].siz) return merge(ls(p),merge(rs(p),q));
		pushdown(rs(p));
		return merge(merge(ls(p),ls(rs(p))),merge(rs(rs(p)),q));
	} else{
		pushdown(q);
		if(4*a[rs(q)].siz>=a[p].siz+a[q].siz) return merge(merge(p,ls(q)),rs(q));
		pushdown(ls(q));
		return merge(merge(p,ls(ls(q))),merge(rs(ls(q)),rs(q)));
	}
}
void split(ll p,ll k,ll &x,ll &y){
	if(isleaf(p)){
		if(k==1) x=p, y=0;
		else x=0, y=p;
		return;
	} pushdown(p);
	if(a[ls(p)].siz>=k){
		split(ls(p),k,x,y);
		y=merge(y,rs(p));
	} else{
		split(rs(p),k-a[ls(p)].siz,x,y);
		x=merge(ls(p),x);
	}
}
int main(){ 
	rt[0]=Newnode(0);
	scanf("%lld",&n);
	for(ll i=1,lst=0;i<=n;i++){
		scanf("%lld%lld%lld",&t,&op,&x); x^=lst;
		rt[i]=rt[t];
		if(op==1){
			scanf("%lld",&y); y^=lst;
			ins(rt[i],x,y);
		} else if(op==2){
			del(rt[i],x);
		} else if(op==3){
			scanf("%lld",&y); y^=lst;
			split(rt[i],y,s1,s3);
			split(s1,x-1,s1,s2);
			a[s2].rev^=1;
			rt[i]=merge(merge(s1,s2),s3);
		} else{
			scanf("%lld",&y); y^=lst;
			split(rt[i],y,s1,s3);
			split(s1,x-1,s1,s2);
			printf("%lld\n",lst=a[s2].sum);
		}
	}
	return 0;
}

此处 fhq-treap 与 WBLT 的比较

测试点编号	WBLT	fhq-treap
1	$9 m s$	$9 m s$
2	$8 m s$	$9 m s$
3	$9 m s$	$9 m s$
4	$8 m s$	$9 m s$
5	$9 m s$	$9 m s$
6	$9 m s$	$9 m s$
7	$303 m s$	$378 m s$
8	$294 m s$	$380 m s$
9	$295 m s$	$379 m s$
10	$298 m s$	$388 m s$
11	$293 m s$	$383 m s$
12	$315 m s$	$372 m s$
13	$292 m s$	$356 m s$
14	$286 m s$	$351 m s$
15	$281 m s$	$352 m s$
16	$282 m s$	$352 m s$
17	$289 m s$	$347 m s$
18	$288 m s$	$340 m s$
19	$297 m s$	$338 m s$
20	$294 m s$	$339 m s$
21	$278 m s$	$280 m s$

不难发现 WBLT 还是比较快的。

一个小优化

在 pushdown 下放标记时，设当前点为 $p$ ，若 $p$ 在持久化 WBLT 上是 $l s (p)$ 的唯一父亲，我们便并不需要新建结点。

具体的，对于每个点记录一个 use，表示该点父亲数量。若 use $\leq 1$ 则不需要新建点，否则新建一个点，新的 use 赋为 $1$ ，原来点的 use 减一。

在复制一个点时，令两个儿子的 use 加一。

总结#

WBLT 还算是比较优秀的平衡树，时间复杂度一般优于 (fhq-)Treap 和 Splay，可能和替罪羊差不多吧。但是 WBLT 支持完全持久化，这就超越了许多的平衡树。

简单来说，除了 LCT，处处可用 WBLT。

一些例题#

CF702F T-Shirts#

题意：一个序列 $a_{1. . . n}$ ，多次询问，每次给出一个数 $k$ ，从 $1. . . n$ 扫描每个 $a_{i}$ ，若 $k \geq a_{i}$ 则 $k \leftarrow k - a_{i}$ ，问一共减了多少次。 $1 \leq n \leq 2 \times 5$

考虑 dp。设 $f [i, j]$ 表示从 $i$ 开始扫，当前数字为 $j$ ，会减多少次。

若 $j < a_{i}$ ，则 $f [i, j] = f [i + 1, j]$ ；若 $j \geq a_{i}$ ，则 $f [i + 1, j - a_{i}] + 1$ 。

相当于把 $f [i + 1, 0. . . a_{i} - 1]$ 这部分原封不动复制过来，然后 $f [i + 1,]$ 整个数组往右移 $a_{i}$ 位并 $+ 1$ 放到 $f [i, a_{i} . . .]$ 。

可以用持久化 WBLT 实现数组 $+ 1$ 和数组合并。

但是至今仍然过不了，毕竟这玩意空间是问题。

经过几个小时的大战，我终于过了。

只需要合并随机化即可。

点击查看代码

#include<bits/stdc++.h>
#define ls(p) a[p].lc
#define rs(p) a[p].rc
#define fi first
#define se second
#define mkp make_pair
#define ll int
#define pir pair<ll,ll>
#define pb push_back
#define ls(p) a[p].lc
#define rs(p) a[p].rc 
using namespace std;
const ll maxn=2e5+10, M=53e6+10, inf=1e9+3;
const double alpha=0.25;
struct WBLT{
	ll rt[maxn],tot;
	struct node{
		ll lc,rc,tag,use;
		ll siz;
	}a[M];
	void pushup(ll p){
		a[p].siz=a[ls(p)].siz+a[rs(p)].siz;
		if(a[p].siz>inf) a[p].siz=inf;
	}
	bool isleaf(ll p){
		return !ls(p)||!rs(p);
	}
	void refresh(ll &p){
		if(a[p].use<=1) return;
		--a[p].use;
		a[++tot]=a[p]; p=tot;
		++a[p].use;
		if(!isleaf(p)) ++a[ls(p)].use, ++a[rs(p)].use;
	}
	void pushdown(ll p){
		if(isleaf(p)||!a[p].tag) return;
		refresh(ls(p));
		refresh(rs(p));
		a[ls(p)].tag+=a[p].tag, a[rs(p)].tag+=a[p].tag;
		a[p].tag=0;
	}
	ll merge(ll p,ll q){
		if(!p||!q) return p|q;
		if(min(a[p].siz,a[q].siz)>=alpha*(a[p].siz+a[q].siz)||rand()<10000){
			ll x=++tot;
			ls(x)=p, rs(x)=q;
			++a[p].use, ++a[q].use;
			pushup(x); return x;
		}
		if(a[p].siz>=a[q].siz){
			pushdown(p);
			if(a[ls(p)].siz>=alpha*(a[p].siz+a[q].siz)||rand()<10000) return merge(ls(p),merge(rs(p),q));
			else{
				pushdown(rs(p));
				return merge(merge(ls(p),ls(rs(p))),merge(rs(rs(p)),q));
			}
		} else{
			pushdown(q);
			if(a[rs(q)].siz>=alpha*(a[p].siz+a[q].siz)||rand()<10000) return merge(merge(p,ls(q)),rs(q));
			else{
				pushdown(ls(q));
				return merge(merge(p,ls(ls(q))),merge(rs(ls(q)),rs(q)));
			}
		}
	}
	void split(ll p,long long k,ll &x,ll &y){
		if(isleaf(p)){
			if(k==0) y=p, x=0;
			else x=p, y=0;
			return;
		}
		pushdown(p);
		if(a[ls(p)].siz>=k){
			split(ls(p),k,x,y);
			y=merge(y,rs(p));
		} else{
			split(rs(p),k-a[ls(p)].siz,x,y);
			x=merge(ls(p),x);
		}
	}
	ll query(ll p,ll k){
		if(isleaf(p)) return a[p].tag;
		pushdown(p);
		if(a[ls(p)].siz>=k) return query(ls(p),k);
		return query(rs(p),k-a[ls(p)].siz);
	}
}T;
struct Ts{
	ll c,q;
}b[maxn];
bool cmp(Ts a,Ts b){
	return a.q==b.q? a.c<b.c:a.q>b.q;
}
ll n,m,w[maxn];
int main(){ 
	scanf("%d",&n); srand(time(0));
	for(ll i=1;i<=n;i++){
		scanf("%d%d",&b[i].c,&b[i].q);
	}
	sort(b+1,b+1+n,cmp);
	T.rt[n+1]=T.tot=1;
	T.a[1].siz=1;
	for(ll i=1;i<=30;i++) T.rt[n+1]=T.merge(T.rt[n+1],T.rt[n+1]);
	for(ll i=n;i;i--){
		ll s1=0, s2=0;
		T.split(T.rt[i+1],b[i].c,s1,s2);
		T.a[++T.tot]=T.a[T.rt[i+1]];
		++T.a[T.tot].tag;
		T.rt[i]=T.merge(s1,T.tot);
	}
	scanf("%d",&m);
	for(ll i=1;i<=m;i++){
		ll x; scanf("%d",&x);
		printf("%d ",T.query(T.rt[1],x+1));
	}
	return 0;
}

出处：https://www.cnblogs.com/Sktn0089/p/18009219

版权：本作品采用「署名-非商业性使用-相同方式共享 4.0 国际」许可协议进行许可。

posted @ 2024-02-06 10:01 Lgx_Q 阅读(362) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· LCT详解（2022修）

· 析合树小记

· 【模板】可持久化的 WBLT

· 从 Leafy-Tree 到 WBLT

· Weight Balanced Leafy Tree 学习笔记

阅读排行：
· 无需6万激活码！GitHub神秘组织3小时极速复刻Manus，手把手教你使用OpenManus搭建本
· C#/.NET/.NET Core优秀项目和框架2025年2月简报
· Manus爆火，是硬核还是营销？
· 一文读懂知识蒸馏
· 终于写完轮子一部分：tcp代理了，记录一下

公告

昵称： Lgx_Q
园龄： 1年7个月
粉丝： 27
关注： 23

+加关注

2025年3月

日

一

二

三

四

五

六

Loading

Lgx_

一种神奇的平衡树——WBLT

Leafy Tree#

维护平衡#

更常规的操作#

持久化操作#

总结#

一些例题#

CF702F T-Shirts#

公告

搜索

常用链接

我的标签

随笔档案

阅读排行榜

评论排行榜

推荐排行榜

最新评论