模拟赛10.11 解题报告
T1 染色#
题意:给出
我们通过爆搜发现对于
由于样例直接给出
T2 序列#
题意:
考场写了一个错解。
枚举
但是会超时,感性认为这是一个单峰函数,考虑直接二分。
被卡
正解咕着。
T3 树上询问#
题意:一棵树,
一眼
考虑拆成
对于第一部分,需满足
对于第二部分,需满足
把询问标记放到
T4 莫队#
题意:一个序列
-
1 x y修改 -
2 l r查询
设
设
对于每个询问
-
对于
-
对于
第一部分的贡献为
第二部分的贡献为
现在有三个问题:
-
动态修改,动态维护
-
快速找出分界点
-
快速查询
对于第一个问题,考虑在值域上搞,设
修改
删除
插入
可以用
对于第二个问题,我们考虑对
对于第三个问题,我们不禁想到经典题——Luogu4198 楼房重建,这里使用兔队线段树维护前缀最大值之和即可。
时间复杂度
出处:https://www.cnblogs.com/Sktn0089/p/17757279.html
版权:本作品采用「署名-非商业性使用-相同方式共享 4.0 国际」许可协议进行许可。

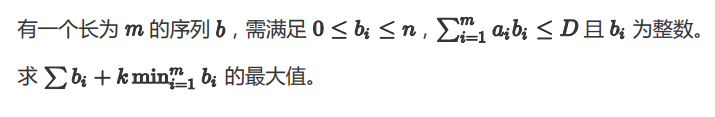



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】