一般图最大匹配——带花树算法

一般图最大匹配问题

---

题意：给出一张无向图，求出最大匹配的匹配数。$1\le |V|,|E|\le {10}^3$

我们学过，二分图最大匹配有个算法——匈牙利算法，其主要思想就是枚举起点，不断寻找增广路，然后把找出的路径匹配状态取反，即可多出一个匹配。

当这个图存在奇环时，就不是二分图了，也就不能使用匈牙利算法。

容易发现，我们的增广路径不能经过奇环，否则就不符合匹配的条件了。

奇环的情况非常复杂，如果仍使用 $\text{DFS}$ 的方法搜索增广路，我们不能保证时间复杂度——因为遇到奇环后不能简单地退出，奇环上的任意一点都可以成为向环外增广的点，时间复杂度可能会炸裂。

用 $\text{BFS}$，我们并不能简单判断搜到的路径是否走过一整个奇环。我们需要更强大的算法——带花树算法。

算法思想

采用 $\text{BFS}$ 的方法。我们要先做没有奇环的情况，所以需要进行黑白染色。设 $vis[u]$ 表示点 $u$ 的状态，$vis[u]=0$ 表示没有访问过，$vis[u]=1/2$ 表示（黑/白）颜，设 $mch[u]$ 表示 $u$ 匹配的点色。根据匈牙利算法的思想，我们只需要把 $vis[u]=1$ 的点 $u$ 放进队列里搜索即可。当搜到一条边 $u,v$ 满足 $vis[u]=vis[v]=1$，设 $rt$ 表示 $u,v$ 在搜索树上的 $\text{LCA}$，那么 $rt-u-v-rt$ 形成了一个奇环。

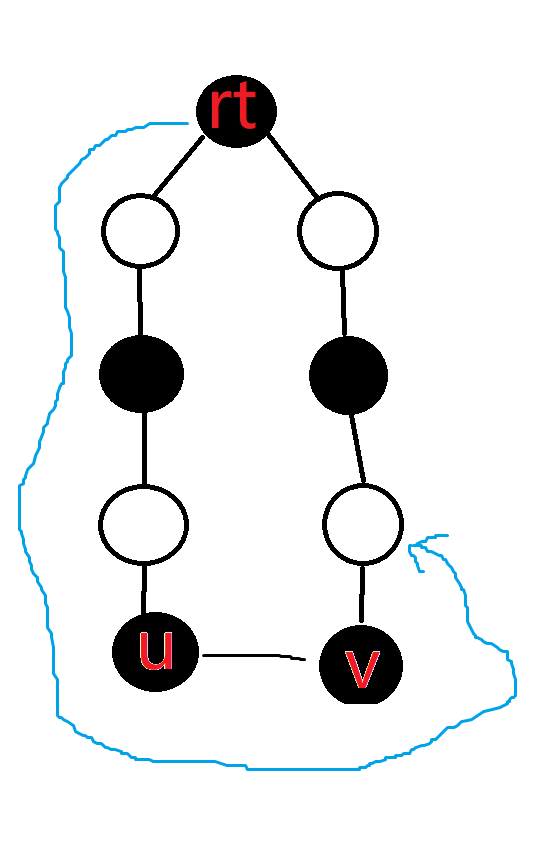
此时我们搜的增广路径经过了这个奇环，设增光路从这个奇环出来的点为 $x$（从 $x$ 搜出的必要条件为 $vis[x]=1$），不难发现，$x$ 可以取所有点。对于黑点，结论显然成立；对于白点，我们显然可以从这个环的另一边走过来。

考虑把这个奇环上的点的 $vis$ 全部改成 $1$，在队列里加入相应的点。记 $pre[u]$ 表示搜索树上 $u$ 的前驱（为了简便，我们只考虑 $vis[u]=2$ 的 $u$ 的前驱），我们求 $\text{LCA}$ 和处理奇环上的点都可以暴力搞。

在更一般的情况，我们可能存在“奇环套奇环”的情况，考虑用一个并查集维护，设 $d[u]$ 表示点 $u$ 所在的奇环的 $\text{LCA}$（严格来说不是 $\text{LCA}$……，应该是环上最接近搜索起点的那个点），我们求 $u,v$ 的 $\text{LCA}$ 时，每次暴力跳可以先用并查集找到所在奇环的根。

为了简便处理更多情况，在一个奇环上，对于原来非匹配边上的两点 $x,y$，令 $pre[x]=y,pre[y]=x$（具体地……因为当 $vis[u]=1$ 时我们没有把 $pre[u]$ 赋值，所以可能会遇到 $pre[u]=0$ 的情况，我们需要处理这种情况）。

综上，对于处理一个奇环，我们分为两部分：

• 找 $u,v$ 在搜索树上的 $\text{LCA}$。

• 把奇环上的点的 $pre$ 值处理一下，把 $vis=2$ 的点加入队列并改为 $1$。

ll lca(ll u,ll v) //找 LCA
{
	++T; //第 T 次找 LCA
	u=find(u); v=find(v);
	while(dfn[u]!=T)
	{
		dfn[u]=T; //跳过的点打标记
		u=find(pre[mch[u]]);
		if(v) swap(u,v); //u,v 轮流向上跳
	}
	return u;
}
void shrink(ll u,ll v,ll rt) //更新奇环上的点的信息
{
	while(find(u)!=rt)
	{
		pre[u]=v; v=mch[u]; //更新 vis=1 的点的 pre 值
		if(vis[v]==2) //把 vis=2 的点加入队列并改成 1
		{
			vis[v]=1; q[++r]=v;
		}
		if(find(u)==u) d[u]=rt; // 把奇环里面的点的并查集信息更新
		if(find(v)==v) d[v]=rt;
		u=pre[v];
	}
}

除了处理奇环，当我们找到增广路后，暴力更新路径：

void aug(ll u)
{
	ll tmp;
	while(u)
	{
		tmp=mch[pre[u]];
		mch[u]=pre[u]; mch[pre[u]]=u;
		u=tmp;
	}
}

总代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const ll maxn=1e5+10;
ll n,m,u,v,ans,head[maxn],tot,pre[maxn],mch[maxn],q[maxn],l,r,vis[maxn],d[maxn],dfn[maxn],T;
struct edge
{
	ll v,nxt;
}e[maxn];
void insert(ll u,ll v)
{
	e[++tot]=(edge){v,head[u]};
	head[u]=tot;
}
ll find(ll x)
{
	if(d[x]==x) return x;
	return d[x]=find(d[x]);
}
ll lca(ll u,ll v)
{
	++T;
	u=find(u); v=find(v);
	while(dfn[u]!=T)
	{
		dfn[u]=T;
		u=find(pre[mch[u]]);
		if(v) swap(u,v);
	}
	return u;
}
void shrink(ll u,ll v,ll rt)
{
	while(find(u)!=rt)
	{
		pre[u]=v; v=mch[u];
		if(vis[v]==2)
		{
			vis[v]=1; q[++r]=v;
		}
		if(find(u)==u) d[u]=rt;
		if(find(v)==v) d[v]=rt;
		u=pre[v];
	}
}
void aug(ll u)
{
	ll tmp;
	while(u)
	{
		tmp=mch[pre[u]];
		mch[u]=pre[u]; mch[pre[u]]=u;
		u=tmp;
	}
}
ll bfs(ll s)
{
	for(ll i=1;i<=n;i++) pre[i]=vis[i]=0, d[i]=i;
	q[l=r=1]=s; vis[s]=1;
	while(l<=r)
	{
		ll u=q[l++];
		for(ll i=head[u];i;i=e[i].nxt)
		{
			ll v=e[i].v;
			if(vis[v]==0)
			{
				pre[v]=u;
				if(!mch[v])
				{
					aug(v);
					return 1;
				}
				else
				{
					vis[v]=2; vis[mch[v]]=1;
					q[++r]=mch[v];
				}
			}
			else if(vis[v]==1&&find(u)!=find(v))
			{
				ll rt=lca(u,v);
				shrink(u,v,rt);
				shrink(v,u,rt);
			}
		}
	}
	return 0;
}
int main()
{
	scanf("%lld%lld",&n,&m);
	for(ll i=1;i<=m;i++)
	{
		scanf("%lld%lld",&u,&v);
		insert(u,v);
		insert(v,u);
	}
	for(ll i=1;i<=n;i++)
		if(!mch[i]) ans+=bfs(i);
	printf("%lld\n",ans);
	for(ll i=1;i<=n;i++) printf("%lld ",mch[i]);
	return 0;
}