【学习笔记】WQS二分
又是DP...
WQS二分学习笔记
前情提要
CSP-S 2022 考场上惊奇的发现最后十几天中90%的时间都在复习的DP竟然根本没考（除了根本不会的DDP），考前没怎么（根本没）复习的最短路和数据结构竟然全部中招，但无论如何作为“算法竞赛的宠儿”的DP依旧是我较为喜欢的一部分内容，因此特地学习一些没有接触过的DP相关的内容
注：喜欢的另一部分内容为高级数据结构 图论去死 long long去死
WQS其人 && 参考文献
王钦石，哈三中巨佬，（曾经的）同省国集神犇，在2012国家集训队论文《浅谈一类二分方法》中首次提出这一算法
原文晦涩难懂，十分简短而且找到的TM要VIP看不了 因此参考了其他几篇博客
感谢 感谢 感谢 以及 十分感谢 差不多各个博客网站的都有了属于是
有什么用
一般用来处理一些带有限制的问题 例如
有\(n\)个物品，物品\(i\)的权重为\(w_i\)。我们需要从中正好选择\(k\)件物品，要求取出的物品总权重最大/最小
怎么去用
我们设\(dp_i\)为选i个物品时的最大收益，可得
理解一下，我们要使\(dp_i\)更大,假设产生选第\(i+1\)件物品\(a\)产生的收益为\(x=dp_{i+1}-dp_i\)，而选择第\(i\)件物品\(b\)产生的收益为\(y=dp_i-dp_{i-1}\)，可以知道要使当前的收益最大化，那么当前选的一定是剩下的里面收益最大的，即我当前选的物品\(b\)的收益\(y\)一定要大于等于我下一个选的物品\(a\)的收益\(x\)
因此两次选择之间的差值是有单调性的（这里是单调递减），可以把\((i,dp_i)\)看做平面直角坐标系上的点，可得以下内容
点\((i-1,dp_{i-1})\)与点\((i,dp_i)\)之间的斜率为\(\frac{dp_i-dp_{i-1}}{i-(i-1)}=dp_i-dp_{i-1}\)，我们已知\(dp_{i+1}-dp_i\leq dp_i-dp_{i-1}\)，因此斜率是单调递减的（非严格），根据斜率优化之前学过的可以知道形成了一个凸包（这里是上凸包）
如何实现
因为斜率具有单调性，可以得到斜率的图像大概的形状（一个目前求不出来的凸包），我们要找到点\((k,dp_k)\)，可以对斜率进行二分查找直到与图像相切的点
如图，图片来自这里
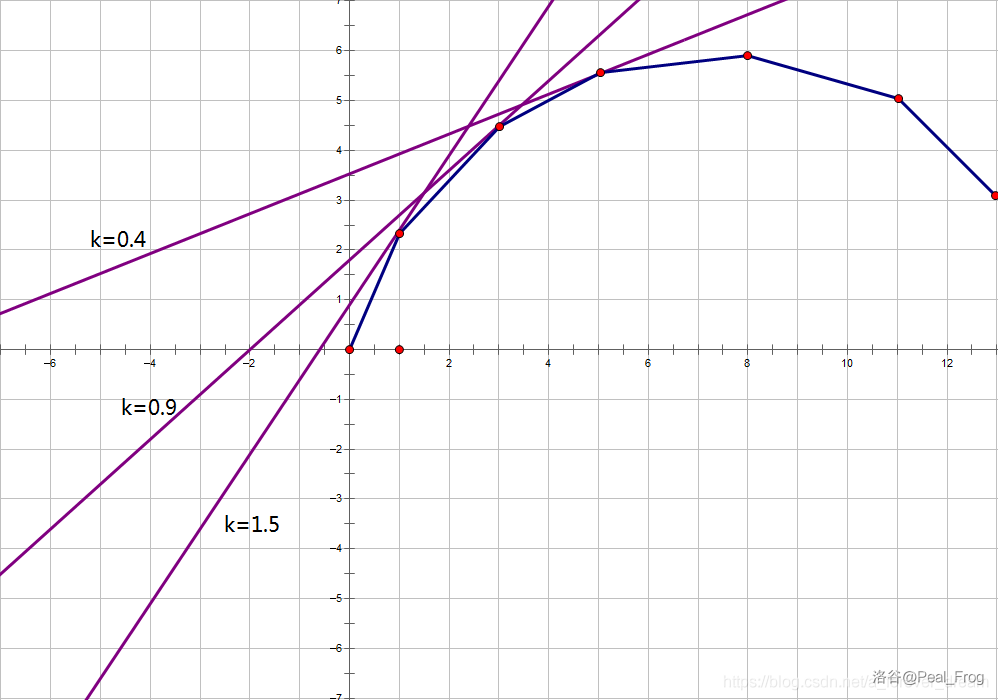
然后二分找到切点
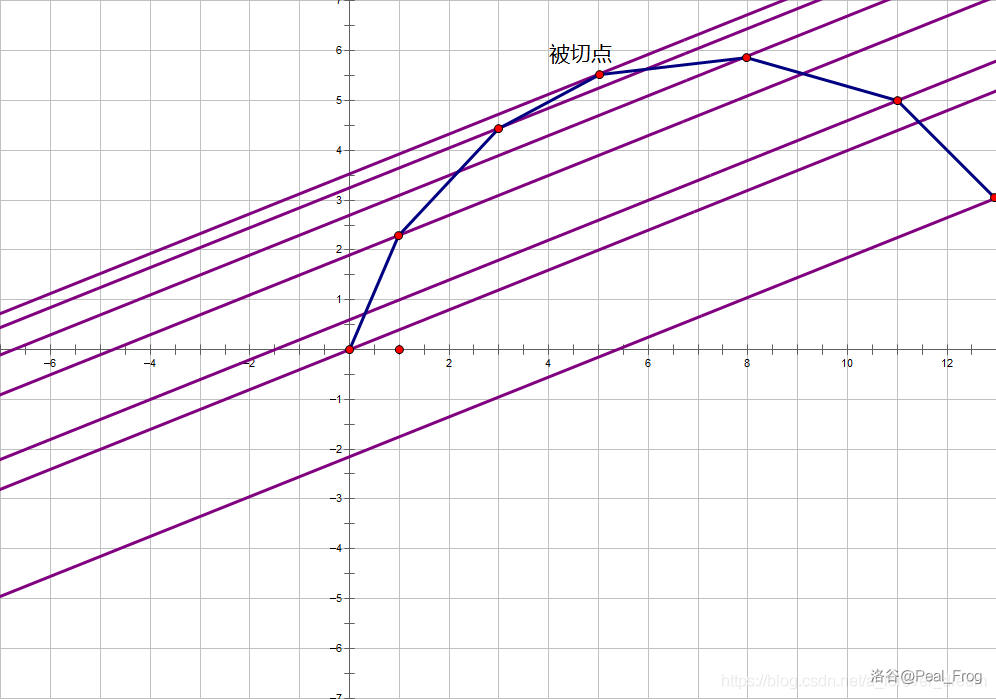
切点又不一定满足\(x=k\)，为什么要找到切点呢？我们思考一下这个函数有什么意义
设斜率为\(c\)，我们用直线切凸包,可以得到解析式\(y=c\times x+b\)，易得到\(b=y-c\times x\)，此时我们可以看做选\(x\)个物品，每个物品的代价为\(val_i-c\)，此时我们忽略个数的限制，对于目前check的\(c\)，可以求一下最大的减去代价后的总权值，以这个总权值为纵截距，我们在选择的时候可以容易统计出来选了多少个物品，即x，如果x小于我要选择的数量，根据单调性，说明k大了，否则说明k小了，这样可以找出最合适的斜率，最终答案为\(y=c\times x+b\)
存在问题
如果最终的斜率是实数怎么办？实数二分？有大佬证明过会T
我们想一下是否真的需要得到精确的斜率？
某dalao云:"我们二分，当选的物品个数≥m时我们更新答案，同时排序上做点手脚"
因为一个范围内切出来k对应的整数大多都在一个x点上
经典例题
【国家集训队】Tree I
WQS在论文中的练习题，在最小生成树上跑wqs即可，这题和DP没什么太大关系
将所有要选择的白边加上一个值mid，因为我们跑一边MST，得到的树中不一定有正好need条白边，加上二分一个mid,看什么时候加上的mid能够使MST中正好有need条白边，找出这时的生成树的权值，最后减去每条边加上的mid即为最终答案
AC code
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<algorithm>
#include<ctime>
using namespace std;
const int maxn=1e5+5;
inline int read()
{
int w=0,f=1;
char ch=getchar();
while(ch<'0' || ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9')
{
w=(w<<3)+(w<<1)+(ch^48);
ch=getchar();
}
return w*f;
}
int fa[maxn];
int V,E,k,tot,ans;
int head[maxn];
struct edge
{
int to,col;
int from,val;
}e[maxn];
bool cmp(edge a,edge b)
{
if(a.val==b.val)
{
return a.col<b.col;
}
return a.val<b.val;
}
int find(int x)
{
if(x==fa[x]) return x;
else return fa[x]=find(fa[x]);
}
void merger(int x,int y)
{
srand(time(0));
if(rand()%2) fa[y]=x;
else fa[x]=y;
}
int kruskal()
{
for(int i=1;i<=V;i++)
{
fa[i]=i;
}
sort(e+1,e+E+1,cmp);
ans=0;int cnt=0,wheit_cnt=0;
for(int i=1;i<=E;i++)
{
int u=find(e[i].from);
int v=find(e[i].to);
if(u==v) continue;
merger(u,v);
if(e[i].col==0) wheit_cnt++;
cnt++;
ans+=e[i].val;
if(cnt==V-1) break;
}
return wheit_cnt;
}
bool check(int mid)
{
for(int i=1;i<=E;i++)
{
if(e[i].col==0)
{
e[i].val+=mid;
}
}
bool res=(kruskal()>=k);
for(int i=1;i<=E;i++)
{
if(e[i].col==0)
{
e[i].val-=mid;
}
}
return res;
}
int main()
{
V=read(),E=read(),k=read();
for(int i=1;i<=E;i++)
{
e[i].from=read()+1;
e[i].to=read()+1;
e[i].val=read();
e[i].col=read();
}
int l=-100,r=100;
int mid_ans;
while(l<=r)
{
int mid=(l+r)>>1;
if(check(mid))
{
l=mid+1;
mid_ans=mid;
}
else
{
r=mid-1;
}
}
check(mid_ans);
cout<<ans-mid_ans*k;
return 0;
}
课下练习
总而言之
WQS是一个非常好用的优化技巧，不只是DP，其他很多方面都可以用到WQS二分，而且经常会与费用流（我还不会）结合起来使用
最后说一句 望CCF数据水一些，long long别卡的太严
UPD 2022-11-2
感觉自己之前的理解有点问题，补充一下精简版
大体上就是二分一个偏移量delta，强制让每一个物品都加上这个偏移量，然后进行没有限制的做法，最后判断选了几个物品，是不是等于k个，否则调整偏移量（二分）
