【集训总结】CSP-S 2022 机房集训总结
CSP-S 2022 校内集训
Day -18
【LNOI 2014】LCA/【GXOI/GZOI 2019】旧词
单独写了篇题解 点这里
【NOIP 2016】天天爱跑步
被称为“NOIP史上最毒瘤题目”
题意大概是是给你一棵树,每个节点都有个观察员盯着,而每个节点的观察员只在特定的时间内盯着你,再给你一些路径,速度是每个时刻走过一条边,问你第i个观察员能看到多少个人
关于路径,给出的两点s和t,由于是在树上两点间的最短路径,必然会经过两点的LCA,(树剖)预处理出两点间的LCA
统计贡献,如果枚举每个路径,然后再去看路径上的观察员对路径产生的贡献,基本上就是\(O(n\times m)\)的暴力,\(3e5\times 3e5\)肯定是会T掉滴,果断放弃。我们可以反着考虑,就是考虑路径对观察员产生的贡献
路径对节点i产生的贡献主要分为一下两种情况
1.i在起点向上到LCA的路径上,若起点对i有贡献,则起点的深度为deep[i]+w[i],这个蛮好理解
2.i在LCA向下到终点的路径上,若终点对i有贡献,则终点的深度为w[i]-deep[i],这个也好理解
就是\(deep[u]+deep[v]-2\times deep[LCA]-deep[v]=w[i]-deep[i]\),其中\(deep[u]+deep[v]-2\times deep[LCA]\)是利用树上差分的思想来求u到v的距离(u为起点,v为终点),我们对每个深度上的节点产生的贡献开两个桶来维护,分别是上行贡献与下行贡献
然后就是一些细节
如果起点/终点对LCA会产生贡献,则统计过程中将会进行重复计算,提前减掉就好
由于桶在这里是递归更新且没有清空,则将会进行大量重复计算以及历史上的遗留,我们应对其进行差分统计答案(其实就是这次统计后的结果减去统计前的结果)
假设有一种情况下当前进行递归的子树以节点P为根,而其中的路径没有经过P节点,那么这条路径是对子树中的一些其他节点产生了贡献,并没有对P产生贡献,更不会对回溯过程中遇到的其他节点产生贡献,所以这条路径只对当前的子树有意义,那么我们应该及时删除这条路径的贡献,否则将会影响对后续回溯过程中遍历的节点贡献的统计,而当前的子树的根应为路径两短点的LCA
简言之,对于以当前遍历的节点为LCA的两个端点形成的路径,只对当前的节点形成的子树产生贡献,应在回溯前减去其贡献,从而消除对接下来回溯过程中统计贡献不应该产生的贡献
最后就是用桶记录下行贡献的下标w[i]-deep[i]可能会产生负数,要对其加上maxn值避免负数导致RE
AC code
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<vector>
#include<algorithm>
#define int long long
using namespace std;
const int maxn=3e5+5;
inline int read()
{
int w=0,f=1;
char ch=getchar();
while(ch<'0' || ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9')
{
w=(w<<3)+(w<<1)+(ch^48);
ch=getchar();
}
return w*f;
}
int n,m,tot;
int dis[maxn];
int head[maxn];
int ans[maxn];
struct edge
{
int to,next;
}e[maxn*2];
int w[maxn];
struct gamer
{
int s,t;
}g[maxn];
void add(int x,int y)
{
e[++tot].to=y;
e[tot].next=head[x];
head[x]=tot;
}
int cnt[maxn];
int bucket_1[maxn*2];
int bucket_2[maxn*2];
int fa[maxn],id[maxn];
int siz[maxn],deep[maxn];
int max_son[maxn],top[maxn];
vector <int> end_e[maxn];
vector <int> LCA_e[maxn];
void dfs_first(int x,int f)
{
siz[x]=1;fa[x]=f;
deep[x]=deep[f]+1;
for(int i=head[x];i;i=e[i].next)
{
int to=e[i].to;
if(to==f) continue;
dfs_first(to,x);
siz[x]+=siz[to];
if(siz[to]>siz[max_son[x]]) max_son[x]=to;
}
}
void dfs_second(int x,int t)
{
id[x]=++tot;top[x]=t;
if(!max_son[x]) return ;
dfs_second(max_son[x],top[x]);
for(int i=head[x];i;i=e[i].next)
{
int to=e[i].to;
if(to!=fa[x] && to!=max_son[x]) dfs_second(to,to);
}
}
int LCA(int x,int y)
{
while(top[x]!=top[y])
{
if(deep[top[x]]<deep[top[y]])
{
swap(x,y);
}
x=fa[top[x]];
}
if(deep[x]>deep[y]) swap(x,y);
return deep[x]<deep[y] ? x : y;
}
void dfs(int x)
{
int cnt_1=bucket_1[deep[x]+w[x]];
int cnt_2=bucket_2[w[x]-deep[x]+maxn];
for(int i=head[x];i;i=e[i].next)
{
int to=e[i].to;
if(to==fa[x]) continue;
dfs(to);
}
bucket_1[deep[x]]+=cnt[x];
for(int i=0;i<end_e[x].size();i++)
{
int path=end_e[x][i];
bucket_2[dis[path]-deep[g[path].t]+maxn]++;
}
ans[x]+=bucket_1[w[x]+deep[x]]-cnt_1+bucket_2[w[x]-deep[x]+maxn]-cnt_2;
for(int i=0;i<LCA_e[x].size();i++)
{
int path=LCA_e[x][i];bucket_1[deep[g[path].s]]--;
bucket_2[dis[path]-deep[g[path].t]+maxn]--;
}
}
signed main()
{
n=read();m=read();
for(int i=1;i<n;i++)
{
int u=read(),v=read();
add(u,v); add(v,u);
}
tot=0,dfs_first(1,0);
tot=0,dfs_second(1,1);
for(int i=1;i<=n;i++)
{
w[i]=read();
}
for(int i=1;i<=m;i++)
{
g[i].s=read();g[i].t=read();
int lca=LCA(g[i].s,g[i].t);
dis[i]=deep[g[i].s]+deep[g[i].t]-deep[lca]*2;
cnt[g[i].s]++; end_e[g[i].t].push_back(i);
LCA_e[lca].push_back(i);
if(deep[lca]+w[lca]==deep[g[i].s]) ans[lca]--;
}
dfs(1);
for(int i=1;i<=n;i++) cout<<ans[i]<<" ";
return 0;
}
Day -17
【SCOI 2013】摩托车交易
听钟神(zhx)讲课说这题和货车运输一模一样,可以直接复制粘贴的内种,然后我就复制粘贴了。。。
然后看了下题发现连输入都不一样,【数据删除】
思路就是kruskal重构树和树剖
对于题目给出的两种限制,我们完全可以不考虑,因为买入交易是不需要输出的
我们完全可以每次贪心的全拿走,全卖出,然后路上扔掉拿不了的(被限制住的),而有列车站的城市之间可以拿无穷多的黄金,那么两种限制就没有存在的意义,唯一的限制就是路径边权
所以问题可以变为给出一个图,让你使其连通,然后还要求两点之间的边权尽量大,我们可以求一个最大生成树,让边权为高速的载重限制,列车站之间的边权设为INF
那么我们每次能携带的黄金数量就等于上一个城市到这个城市经过的所有边的最小边权和现在有的黄金数量的较小值,路径上边权最小值可以用树剖求解
然后这题就切了QwQ
AC code
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<algorithm>
#include<climits>
#include<cstdlib>
#define int long long
using namespace std;
const int maxn=2e5+5;
inline int read()
{
int w=0,f=1;
char ch=getchar();
while(ch<'0' || ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9')
{
w=(w<<3)+(w<<1)+(ch^48);
ch=getchar();
}
return w*f;
}
int now_money;
int root,cnt;
int n,m,q,tot;
int head[maxn];
int b[maxn];
int fa[maxn];
struct edge
{
int from,to,val;
}e[maxn*3];
struct node
{
int to,next,val;
}edg[maxn*3];
int order[maxn];
bool cmp(edge a,edge b)
{
return a.val>b.val;
}
void add(int x,int y,int z)
{
edg[++tot].to=y;
edg[tot].next=head[x];
edg[tot].val=z;
head[x]=tot;
}
int find(int x)
{
if(x==fa[x]) return x;
else return fa[x]=find(fa[x]);
}
void merger(int x,int y)
{
if(rand()%2) fa[x]=y;
else fa[y]=x;
}
void kruskal()
{
for(int i=1;i<=n;i++) fa[i]=i;
sort(e+1,e+m+max(q,1ll),cmp);cnt=0;
for(int i=1;i<=m+max(q,1ll)-1;i++)
{
int u=find(e[i].from);
int v=find(e[i].to);
if(u==v) continue;
merger(u,v);cnt++;
add(e[i].from,e[i].to,e[i].val);
add(e[i].to,e[i].from,e[i].val);
if(cnt==n-1) break;
}
}
int a[maxn];
int id[maxn],val[maxn];
int siz[maxn],deep[maxn];
int max_son[maxn],top[maxn];
struct s_t
{
int l,r;
int val;
}t[maxn*4];
void dfs_first(int x,int f)
{
siz[x]=1;fa[x]=f;
deep[x]=deep[f]+1;
for(int i=head[x];i;i=edg[i].next)
{
int to=edg[i].to;
if(to==f) continue;
val[to]=edg[i].val;
dfs_first(to,x);
siz[x]+=siz[to];
if(siz[to]>siz[max_son[x]])
{
max_son[x]=to;
}
}
}
void dfs_second(int x,int t)
{
id[x]=++tot;top[x]=t;
a[tot]=val[x];
if(!max_son[x]) return ;
dfs_second(max_son[x],top[x]);
for(int i=head[x];i;i=edg[i].next)
{
int to=edg[i].to;
if(to!=fa[x] && to!=max_son[x])
{
dfs_second(to,to);
}
}
}
void build(int p,int l,int r)
{
t[p].l=l,t[p].r=r;
if(l==r)
{
t[p].val=a[l];
return ;
}
int mid=(l+r)>>1;
build(p*2,l,mid);
build(p*2+1,mid+1,r);
t[p].val=min(t[p*2].val,t[p*2+1].val);
}
int query(int p,int l,int r)
{
if(l<=t[p].l && t[p].r<=r) return t[p].val;
int mid=(t[p].l+t[p].r)>>1;int ans=LLONG_MAX;
if(l<=mid) ans=min(ans,query(p*2,l,r));
if(r>mid) ans=min(ans,query(p*2+1,l,r));
return ans;
}
int get_min(int x,int y)
{
int ans=LLONG_MAX;
while(top[x]!=top[y])
{
if(deep[top[x]]<deep[top[y]]) swap(x,y);
ans=min(ans,query(1,id[top[x]],id[x]));
x=fa[top[x]];
}
if(deep[x]>deep[y]) swap(x,y);
ans=min(ans,query(1,id[x]+1,id[y]));
return ans;
}
signed main()
{
n=read();
m=read();
q=read();
for(int i=1;i<=n;i++)
{
order[i]=read();
}
for(int i=1;i<=n;i++)
{
b[i]=read();
}
for(int i=1;i<=m;i++)
{
e[i].from=read();
e[i].to=read();
e[i].val=read();
}
for(int i=1;i<=q;i++)
{
if(i==1)
{
root=read();
}
else
{
e[m+i-1].from=root;
e[m+i-1].to=read();
e[m+i-1].val=LLONG_MAX;
}
}
kruskal();
tot=0,dfs_first(1,0);
tot=0,dfs_second(1,1);
build(1,1,n);
now_money=b[order[1]];
if(now_money<=0)
{
now_money=0;
cout<<0<<endl;
}
for(int i=2;i<=n;i++)
{
now_money=min(get_min(order[i],order[i-1]),now_money);
if(b[order[i]]<0)
{
cout<<min(now_money,-b[order[i]])<<endl;
now_money-=min(now_money,-b[order[i]]);
}
else
{
now_money+=b[order[i]];
}
}
return 0;
}
Power Tree
给出一棵n个节点的树,每个节点有一个代价,你可以花费这个代价来使以其为根节点的子树内的叶子节点的权值同时增加v(可以为负数),花费最小代价,使其所有叶子节点权值都变为0,输出最小权值及所有可能在最优解内的点
很巧妙的做法,也是钟神上课讲的
对叶子节点权值进行差分,那么每次对节点修改,相当于对一个节点可控制的叶子节点的dfs序的左端点加上v,右端点+1的位置减去v(毕竟是差分么),我们可以产生n个区间[l,r+1],因为要清空权值,相当于把差分序列的权值也清空即可,可以看作对每个区间从l到r+1进行连边,然后把区间[l,r]的权值转移到r+1,最后把dfs序区间[1,n]的权值全部转移到n+1即可,那我们就要保证连边后所有区间是连通的,且代价最小,那么我们就可以对新产生的边求最小生成树,最小生成树的大小就是最小代价
然后再看所有可能在最优解内的点,这一点也是在保证连通的前提下进行的,而之所以是可能是因为可能含有边权相同的边,即大小相等的最小生成树有多种形成的方法,在kruskal求最小生成树的过程中就可以进行判断处理
AC code
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<climits>
#include<string>
#include<cmath>
#include<algorithm>
#define int long long
using namespace std;
const int maxn=200010;
inline int read()
{
int w=0,f=1;
char ch=getchar();
while(ch<'0' || ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9')
{
w=(w<<3)+(w<<1)+(ch^48);
ch=getchar();
}
return w*f;
}
bool ok[maxn];
int head[maxn],n,tot,cnt;
int w[maxn],fa[maxn],ans;
int dfn_l[maxn],dfn_r[maxn];
struct edge
{
int to,next;
}e[maxn*2];
struct node
{
int from,to,val,point;
}edg[maxn];
void add(int x,int y)
{
e[++tot].to=y;
e[tot].next=head[x];
head[x]=tot;
}
void e_add(int x,int y,int p)
{
edg[++tot].from=x,edg[tot].to=y;
edg[tot].val=w[p],edg[tot].point=p;
}
void dfs(int x,int fa)
{
bool check=true;dfn_l[x]=INT_MAX;
for(int i=head[x];i;i=e[i].next)
{
int to=e[i].to;
if(to==fa) continue;
check=false;
dfs(to,x);
dfn_l[x]=min(dfn_l[x],dfn_l[to]);
dfn_r[x]=max(dfn_r[x],dfn_r[to]);
}
if(check)
{
dfn_l[x]=dfn_r[x]=++cnt;
}
e_add(dfn_l[x],dfn_r[x]+1,x);
}
int find(int x)
{
if(x==fa[x]) return x;
return fa[x]=find(fa[x]);
}
void merger(int x,int y)
{
fa[x]=y;
}
bool cmp(node a,node b)
{
return a.val<b.val;
}
void kruskal()
{
for(int i=1;i<=n+1;i++)
{
fa[i]=i;
}
sort(edg+1,edg+n+1,cmp);
int l,r;
for(l=1;l<=n;l=r+1)
{
r=l;
while(r<n && edg[r].val==edg[r+1].val) r++;
for(int i=l;i<=r;i++)
{
int u=edg[i].from,v=edg[i].to;
if(find(u)==find(v)) continue;
cnt++,ok[edg[i].point]=true;
}
for(int i=l;i<=r;i++)
{
int u=find(edg[i].from);
int v=find(edg[i].to);
if(u==v) continue;
merger(u,v);
ans+=edg[i].val;
}
}
}
signed main()
{
n=read();
for(int i=1;i<=n;i++)
{
w[i]=read();
}
for(int i=1;i<n;i++)
{
int u=read();
int v=read();
add(u,v),add(v,u);
}
tot=0,dfs(1,0);
cnt=0,kruskal();
cout<<ans<<" "<<cnt<<endl;
for(int i=1;i<=n;i++)
{
if(ok[i]) cout<<i<<" ";
}
return 0;
}
【CQOI 2007】余数求和
前几天隔离的时候C_liar大佬考了我这道题,后来才得知这玩应叫什么数论分块
\(k\mod i\)可以转化为\(k-\left \lfloor \frac{k}{i} \right \rfloor \times i\)
所以\(\sum_{i=1}^{n}k\mod i\)=\(\sum_{i=1}^{n}k-\left \lfloor \frac{k}{i} \right \rfloor \times i\)
所以答案就是\(k\times n-\sum_{i=1}^{n}\left \lfloor \frac{k}{i} \right \rfloor \times i\)
柿子减号前的一项比较好说,主要说减号之后的
我们可以通过样例打表找规律
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| \(\left \lfloor \frac{k}{i} \right \rfloor\) | 5 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
可以发现在某一特定的区域内,\(\left \lfloor \frac{k}{i} \right \rfloor\)的值是不变的
所以想到了分块,每块的和\(sum=\left \lfloor \frac{k}{i} \right \rfloor \times (r-l+1)\times (l+r)\div 2\) 就是i的平均值乘块长乘\(\left \lfloor \frac{k}{i} \right \rfloor\)
r分情况讨论求出,时间复杂度\(O\sqrt{k}\)
AC code
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,k,ans,l,r,t;
signed main()
{
scanf("%lld%lld",&n,&k);
ans=n*k;
for(int l=1;l<=n;l=r+1)
{
(t=(k/l))?r=min(k/t,n):r=n;
ans-=t*(r-l+1)*(l+r)>>1;
}
cout<<ans;
return 0;
}
Day -16
ABC Transform
给定一个由ABC三种字母组成的字符串,\(S^0=S\),\(S^i\)表示对\(S^{i-1}\)进行操作:A变为BC,B变为CA,C变为AB,询问\(S^t\)的第k个字母
思维题,对于原始字符串的每个字母而言,都相当于形成了一颗二叉树,询问第t层的第k个节点,可以发现对于一个节点,都可以向上递归到最左侧一条链,即\(k=1\)的情况,我们可以发现\(k=1\)时从上到下一定是按照ABC为循环节进行循环,所以当前节点对应字母一定是(初始序列首字母+层数)%3
然后在考虑到达k=1以下时的情况,分为左右子节点来考虑
如果当前节点是左儿子,即\(k\mod 2=1\),我们可以发现其对应字母一定是按照父节点对应字母+1来循环,即\((\frac{k+1}{2}+1)\mod 3\)(A变为B,B变为C,C变为A),否则其对应字母按照父节点对应字母+2来循环,即\((\frac{k+1}{2}+2)\mod 3\)(A变为C,B变为A,C变为B),然后递归求解即可
AC code
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<algorithm>
#define int long long
using namespace std;
inline int read()
{
int w=0,f=1;
char ch=getchar();
while(ch<'0' || ch>'9')
{
if(ch=='-')
{
f=-1;
}
ch=getchar();
}
while(ch>='0' && ch<='9')
{
w=(w<<3)+(w<<1)+(ch^48);
ch=getchar();
}
return w*f;
}
int q;
string str;
char query(int t,int k)
{
if(t==0) return str[k-1];
if(k==1) return 'A'+(str[0]-'A'+t)%3;
if(k%2==0) return 'A'+(query(t-1,(k+1)/2)-'A'+2)%3;
if(k%2==1) return 'A'+(query(t-1,(k+1)/2)-'A'+1)%3;
}
signed main()
{
cin>>str;
q=read();
for(int i=1;i<=q;i++)
{
int t,k;
t=read();
k=read();
cout<<query(t,k)<<endl;
}
return 0;
}
Delivery Club
和上边的那道题一样,都是一位学长在暑假的时候出的模拟赛题,现在才来补
有两个人,初始位置给出,在n个位置上有n个任务,他俩去一个人就行,要求最小化两者之间的产生的最大距离
一眼二分答案,然后check假了,正推无法寻求到正解(当时只有15pts),所以我们只能倒推
我们用区间[l,r]表示两人中一人在\(x_i\)的位置,另一人所在位置的合法范围,然后开始从区间i+1向区间i倒推,最后s1或s2中的一处在区间内即可(另一个人在x[1]处)
存在两种情况
- \(x_i\)位于现在的区间(区间i+1)内,差不多是这个样子
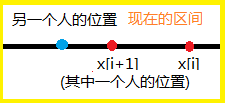
直接让蓝点位置的人过去就行,\(x_i+1\)就在区间\([x_i-mid,x_i+mid]\)内,区间i直接就可以变为\([x_i-mid,x_i+mid]\)
- \(x_i\)不在现在的区间内,那应该满足这个样子
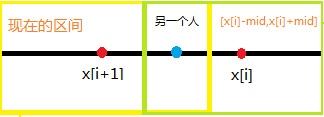
让\(x_{i+1}\)位置的人去\(x_i\),然后另一个人在两个区间的交集即可,新区间就是两区间的交集
然后就这样更新出原始区间,判断s1、s2与区间的关系即可AC
AC code
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<climits>
#include<algorithm>
using namespace std;
const int INF=1e9;
const int maxn=100010;
inline int read()
{
int w=0,f=1;
char ch=getchar();
while(ch<'0' || ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9')
{
w=(w<<3)+(w<<1)+(ch^48);
ch=getchar();
}
return w*f;
}
int n,s1,s2;
int x[maxn];
bool check(int k)
{
int l=-INF,r=INF;
for(int i=n;i>=1;i--)
{
if(l<=x[i] && x[i]<=r)
{
l=x[i]-k,r=x[i]+k;
}
else
{
l=max(l,x[i]-k);
r=min(r,x[i]+k);
}
}
return ((l<=s1 && s1<=r) || (l<=s2 && s2<=r));
}
int main()
{
n=read(),s1=read(),s2=read();
for(int i=1;i<=n;i++) x[i]=read();
int l=abs(s1-s2),r=INF;
while(l<=r)
{
int mid=(l+r)>>1;
if(check(mid)) r=mid-1;
else l=mid+1;
}
cout<<l;
return 0;
}
Minimum Sum
给你一个序列,求\(\sum^{N}_{l=1}\sum^{N}_{r=l}min(a_l,a_{l+1},\dots,a_r)\)
一个技巧就是转化为\(a_i\)对答案的贡献,求出其左右两边的第一个比自己小的值,这让就会产生一个区间,即最长的以\(a_i\)为最小值的区间,然后其所有子区间都以\(a_i\)为最小值,而所有以\(a_i\)为最小值的区间乘\(a_i\)就是\(a_i\)对答案的贡献,最终答案为所有\(a_i\)对答案的贡献之和
左右两边第一个比自己小的值正反跑两遍单调栈即可求出,记得开long long(没开long long挂成30pts)
AC code
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<cstdlib>
#include<algorithm>
#include<queue>
#include<stack>
#include<vector>
#include<map>
#define int long long
using namespace std;
const int maxn=200010;
inline int read()
{
int w=0,f=1;
char ch=getchar();
while(ch<'0' || ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9')
{
w=(w<<3)+(w<<1)+(ch^48);
ch=getchar();
}
return w*f;
}
int n,ans;
int a[maxn];
int l[maxn];
int r[maxn];
stack <int> s;
signed main()
{
n=read();
for(int i=1;i<=n;i++) a[i]=read();
for(int i=1;i<=n;i++)
{
while(!s.empty() && a[s.top()]>=a[i]) s.pop();
if(!s.empty()) l[i]=s.top(); s.push(i);
}
while(!s.empty()) s.pop();
s.push((n+1));
for(int i=n;i>=1;i--)
{
while(!s.empty() && a[s.top()]>=a[i]) s.pop();
if(!s.empty()) r[i]=s.top(); s.push(i);
}
for(int i=1;i<=n;i++) ans+=(r[i]-i)*(i-l[i])*a[i];
cout<<ans;
return 0;
}
小清新人渣的本愿
暑假有幸听lxl讲了十几天课,深受其毒瘤数据结构之害,看到题目提供者就想到了莫队
考虑莫队+bitset
我们开两个bitset,一个来判断\(x\)是否存在,另一个来判断\(N-x\)是否存在,N取到数据范围上限
- 减法操作 \(a-b=x\)
可以转化为\(a-x=b\),然后用第一个bitset判断a与a-x是否同时存在即可 (liv&(liv<<x))是否为1
- 加法操作 \(a+b=x\)
构造一个\(b'=N-b\),所以\(a+N-b'=x\),\(a-b'=x-N\),\(a-(x-N)=b'\),问题就转化为了减法操作,判断a与a-(x-N)是否同时存在 (liv&(rev>>(N-x))是否为1
- 乘法操作 \(a\times b=x\)
直接枚举x的约数i,然后判断i与$ \frac{x}{i} $是否同时存在,应该没有什么更好的方法了吧
AC code
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<bitset>
#include<algorithm>
using namespace std;
const int maxn=1e5+5;
inline int read()
{
int w=0,f=1;
char ch=getchar();
while(ch<'0' || ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9')
{
w=(w<<3)+(w<<1)+(ch^48);
ch=getchar();
}
return w*f;
}
int n,m,N;
int a[maxn];
int siz,num;
int cnt[maxn];
int ans[maxn];
int bel[maxn];
bitset <maxn> liv;
bitset <maxn> rev;
struct que
{
int id,l,r,opt,x;
}q[maxn];
bool cmp(que a,que b)
{
if(bel[a.l]!=bel[b.l])
{
return bel[a.l]<bel[b.l];
}
return a.r<b.r;
}
void add(int x)
{
if(cnt[a[x]]==0)
{
liv[a[x]]=1;
rev[N-a[x]]=1;
}
cnt[a[x]]++;
}
void del(int x)
{
cnt[a[x]]--;
if(cnt[a[x]]==0)
{
liv[a[x]]=0;
rev[N-a[x]]=0;
}
}
int main()
{
n=read(),m=read();
for(int i=1;i<=n;i++)
{
a[i]=read();
}
N=maxn;
siz=sqrt(n),num=ceil((double)n/siz);
for(int i=1;i<=num;i++)
{
for(int j=(i-1)*siz+1;j<=min(n,i*siz);j++)
{
bel[j]=i;
}
}
for(int i=1;i<=m;i++)
{
q[i].id=i,q[i].opt=read();
q[i].l=read(),q[i].r=read();
q[i].x=read();
}
sort(q+1,q+m+1,cmp);
int l=1,r=0;
for(int i=1;i<=m;i++)
{
while(l<q[i].l) del(l++);
while(l>q[i].l) add(--l);
while(r<q[i].r) add(++r);
while(r>q[i].r) del(r--);
int opt=q[i].opt,x=q[i].x;
if(opt==1) ans[q[i].id]=(liv&(liv<<x)).any();
if(opt==2) ans[q[i].id]=(liv&(rev>>(N-x))).any();
if(opt==3)
{
for(int k=1;k*k<=x;k++)
{
if(x%k) continue;
ans[q[i].id]=(liv[k]&&liv[x/k]);
if(ans[q[i].id]) break;
}
}
}
for(int i=1;i<=m;i++)
{
if(ans[i]) cout<<"hana"<<endl;
else cout<<"bi"<<endl;
}
return 0;
}
Day -15
Anonymity Is Important
CF上2200的题,对我来说就这么困难了。。。
然后这题思路真的很妙,尤其是对STL的应用
用0表示这个人确定了没病,1表示这个人可能有点大病
如果是一定有病应该是这样的
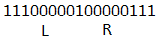
我们起初把所有不确定的人insert进一个set里面,判断是否一定有病也就是需要判断其在set里对应的的前驱l,后继r是否满足存在一个操作二产生的区间[l',r']属于区间(l,r)(这里是开区间,不能取到l,r),可以用线段树维护每个由操作二产生的区间对应的l所可以对应的最小的r,即支持单点修改,区间查询最小值
然后查询时,如果这个人不在set里说明他没病,如果在且有上述区间满足说明他有病,否则不能说他有病,也不能证明他没病
AC code
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<string>
#include<set>
#include<climits>
#include<algorithm>
using namespace std;
const int maxn=2e5+5;
inline int read()
{
int w=0,f=1;
char ch=getchar();
while(ch<'0' || ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9')
{
w=(w<<3)+(w<<1)+(ch^48);
ch=getchar();
}
return w*f;
}
int n,q;
struct s_t
{
int l,r;
int val;
}t[maxn*4];
set <int> s;
void build(int p,int l,int r)
{
t[p].l=l,t[p].r=r,t[p].val=n+1;
if(l==r) return ;
int mid=(l+r)>>1;
build(p*2,l,mid);
build(p*2+1,mid+1,r);
}
void update(int p,int l,int r,int k,int val)
{
if(t[p].l==t[p].r)
{
t[p].val=min(t[p].val,val);
return ;
}
int mid=(t[p].l+t[p].r)>>1;
if(k<=mid) update(p*2,l,r,k,val);
else update(p*2+1,l,r,k,val);
t[p].val=min(t[p*2].val,t[p*2+1].val);
}
int query(int p,int l,int r)
{
if(l<=t[p].l && t[p].r<=r)
{
return t[p].val;
}
int mid=(t[p].l+t[p].r)>>1;
int ans=INT_MAX;
if(l<=mid) ans=min(ans,query(p*2,l,r));
if(r>mid) ans=min(ans,query(p*2+1,l,r));
return ans;
}
int main()
{
n=read();
q=read();
build(1,1,n);
for(int i=0;i<=n+1;i++)
{
s.insert(i);
}
for(int i=1;i<=q;i++)
{
int opt=read();
if(opt==0)
{
int l=read(),r=read(),op=read();
if(op==0)
{
int k=*s.lower_bound(l);
while(!s.empty())
{
int k=*s.lower_bound(l);
if(k<=r) s.erase(k);
else break;
}
}
else
{
update(1,1,n,l,r);
}
}
else
{
int k=read();
if(!s.count(k))
{
cout<<"NO"<<endl;
continue;
}
auto l=s.lower_bound(k);
auto r=s.upper_bound(k);
l--;
if(query(1,*l+1,k)<*r)
{
cout<<"YES"<<endl;
}
else
{
cout<<"N/A"<<endl;
}
}
}
return 0;
}
Meaningful Mean
给你好几个数,然后对于这个序列的所有区间,让你求其平均值大于等于k的区间个数
先用前缀和预处理一下,对于某个区间[l,r]的平均值为\(\frac{sum_r-sum_{l-1}}{r-l+1}\geq k\)
\(sum_r-sum_{l-1}\geq k\times(r-l+1)\),我们可以通过一些操作使k变成零(输入\(a_i\)时都减去k就好啦),可以得到\(sum_r-sum_{l-1}\geq 0\),即\(sum_r\geq sum_{l-1}\),然后就变成了二维偏序(数点),用树状数组处理即可
还有就是sum数组要进行离散化 预处理时要记得把l=1时的贡献统计进去(树状数组会统计不到)
AC code
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<algorithm>
#define int long long
using namespace std;
const int maxn=2e5+5;
inline int read()
{
int w=0,f=1;
char ch=getchar();
while(ch<'0' || ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9')
{
w=(w<<3)+(w<<1)+(ch^48);
ch=getchar();
}
return w*f;
}
int n,k,ans;
int a[maxn];
int sum[maxn];
int cop[maxn];
int tree[maxn];
int lowbit(int x){ return x&-x; }
void update(int x,int y)
{
for(;x<=n;x+=lowbit(x))
{
tree[x]+=y;
}
}
int query(int x)
{
int ans=0;
for(;x;x-=lowbit(x))
{
ans+=tree[x];
}
return ans;
}
signed main()
{
n=read();
k=read();
for(int i=1;i<=n;i++)
{
a[i]=read()-k;
}
for(int i=1;i<=n;i++)
{
sum[i]=sum[i-1]+a[i];
cop[i]=sum[i-1]+a[i];
if(sum[i]>=0) ans++;
}
sort(cop+1,cop+n+1);
int num=unique(cop+1,cop+n+1)-cop-1;
for(int i=1;i<=n;i++)
{
sum[i]=lower_bound(cop+1,cop+n+1,sum[i])-cop;
}
for(int i=1;i<=n;i++)
{
ans+=query(sum[i]);
update(sum[i],1);
}
cout<<ans;
return 0;
}
Day -14/Day -13
先鸽两天,学DP去了
斜率优化好难啊我敲
不过应该是CSP-S前学的最后一个知识点了
Day -12
以后的题都是DP(毕竟是考试重点)
所以搬到了这里
这篇blog就到这里吧
Day -7
【COCI 2017-2018#5】Karte
贪心的发现牌上数字越小的在上面的结果越正确,我们可以将错误的全部放在最后K个
所以先按从小到大排序,在最后k个按从大到小排序
然后就O(n)枚举判断是否恰好等于k即可
AC code
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<algorithm>
using namespace std;
const int maxn=5e5+5;
inline int read()
{
int w=0,f=1;
char ch=getchar();
while(ch<'0' || ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9')
{
w=(w<<3)+(w<<1)+(ch^48);
ch=getchar();
}
return w*f;
}
int n,k,cnt;
int a[maxn];
bool cmp(int x,int y)
{
return x>y;
}
int main()
{
n=read(),k=read();
for(int i=1;i<=n;i++) a[i]=read();
sort(a+1,a+n+1);
sort(a+n-k+1,a+n+1,cmp);
for(int i=n;i>=1;i--)
{
if(cnt<a[i]) cnt++;
}
if(cnt!=k) { cout<<-1;return 0; }
for(int i=1;i<=n;i++) cout<<a[i]<<" ";
return 0;
}
【NOI Online #2 入门组】建设城市
分为两种情况
一种是\(x\leq n\)且\(y>n\)
这种情况枚举x,y的高度i,分成的四个区间,每个区间相当于n栋楼放入i或m-i+1个高度中的方案数(每个高度可空)
另一种情况是x,y同时大于或小于等于n
将x到y之间全部都当做一栋楼,然后按照上述组合数方法分析
(阶乘逆元一定要处理好qwq)
AC code
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<cstdlib>
#include<algorithm>
#define int long long
using namespace std;
const int maxn=2e5+5;
const int mod=998244353;
int fc[maxn];
int ifc[maxn];
int ans,m,n,x,y;
int ksm(int a,int b)
{
int ans=1;
for(;b;b>>=1,a=(a*a)%mod)
{
if(b&1) ans=(ans*a)%mod;
}
return ans;
}
int c(int m,int n)
{
return fc[n+m-1]*ifc[n]%mod*ifc[m-1]%mod;
}
signed main()
{
scanf("%lld%lld%lld%lld",&m,&n,&x,&y);
fc[0]=1;
for(int i=1;i<=n+m;i++)
{
fc[i]=(fc[i-1]*i)%mod;
}
ifc[m+n]=ksm(fc[m+n],mod-2);
for(int i=n+m-1;i>=0;i--)
{
ifc[i]=ifc[i+1]*(i+1)%mod;
}
if(x<=n && y>n)
{
for(int i=1;i<=m;i++)
{
ans=(ans+c(i,x-1)*c(m-i+1,n-x)%mod*c(m-i+1,y-n-1)%mod*c(i,2*n-y)%mod)%mod;
}
}
else
{
ans=c(m,n)*c(m,n+x-y)%mod;
}
cout<<ans;
return 0;
}
【Cnoi 2021】自我主义的平衡者
贪心好题qwq,分别求最大值和最小值
求最小值时肯定更多是要评0的,所以按照降序排序,前面的一定是高于后面心里的预期的,因此大多会评为0分反之亦同理
其实这是我瞎扯的qwq,具体证明不会,但是上述是自己做题想出来的
没想到A了qwq
AC code
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<algorithm>
#define int long long
using namespace std;
const int maxn=1e5+5;
inline int read()
{
int w=0,f=1;
char ch=getchar();
while(ch<'0' || ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9')
{
w=(w<<3)+(w<<1)+(ch^48);
ch=getchar();
}
return w*f;
}
int n,m;
int now_max;
int now_min;
int a[maxn];
bool cmp(int x,int y)
{
return x>y;
}
signed main()
{
n=read(),m=read();
for(int i=1;i<=n;i++) a[i]=read();
sort(a+1,a+n+1);
now_max=m;
for(int i=2;i<=n;i++)
{
if((double)now_max/(i-1) <= a[i]) now_max+=m;
}
sort(a+1,a+n+1,cmp);
for(int i=2;i<=n;i++)
{
if((double)now_min/(i-1) <= a[i]) now_min+=m;
}
double ans_max=(double)now_max/n;
double ans_min=(double)now_min/n;
printf("%.2lf %.2lf",ans_max,ans_min);
return 0;
}
Day -4
A Star not a Tree?
模拟退火板子题,挺好写的 就是UVA比随机化还要玄学
AC code
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<climits>
#include<algorithm>
#define de 0.996
using namespace std;
const int maxn=105;
int t,n;
double kx,ky;
double x,y,ans,ansx,ansy;
double xi[maxn],yi[maxn];
void init()
{
kx=0,ky=0;
ans=1e8;
}
double calc(double x,double y)
{
double ans=0;
for(int i=1;i<=n;i++)
{
ans+=sqrt((xi[i]-x)*(xi[i]-x)+(yi[i]-y)*(yi[i]-y));
}
return ans;
}
void SA()
{
x=ansx,y=ansy;
double t=3000;
while(t>1e-15)
{
double rx=x+((rand()<<1)-RAND_MAX)*t;
double ry=y+((rand()<<1)-RAND_MAX)*t;
double now=calc(rx,ry);
double k=now-ans;
if(k<0)
{
x=rx,y=ry;
ansx=rx,ansy=ry;
ans=now;
}
else
{
if(exp(-k/t)*RAND_MAX>rand())
x=rx,y=ry;
}
t*=de;
}
}
void work()
{
ansx=kx/n;
ansy=ky/n;
SA();
SA();
SA();
SA();
SA();
SA();
}
int main()
{
srand(1e9+7);
cin>>t;
while(t--)
{
cin>>n;
init();
for(int i=1;i<=n;i++)
{
cin>>xi[i],cin>>yi[i];
kx+=xi[i],ky+=yi[i];
}
work();
cout<<round(ans)<<endl;
if(t) cout<<endl;
}
}
Haywire
什么rp啊我这是 随机打乱序列 然后模拟退火 调参交了90遍才A
AC code
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<vector>
#include<algorithm>
#define detal 0.9997
using namespace std;
const int maxn=15;
int n,cnt;
double ans;
struct node
{
int a,b,c;
}nod[maxn];
int num[maxn];
vector <int> g[maxn];
double calc(int *x)
{
cnt++;
double ans=0;
for(int i=1;i<=n;i++)
{
for(int j=0;j<g[x[i]].size();j++)
{
for(int k=1;k<=n;k++)
{
if(x[k]==g[x[i]][j]) ans+=(double)abs(k-i);
}
}
}
return ans/2.0;
}
void SA()
{
int k[maxn];
for(int i=1;i<=n;i++)
{
k[i]=num[i];
}
double t=3000;
while(t>1e-15)
{
random_shuffle(k+1,k+1+n);
double rans=calc(k);
double E_Detal=rans-ans;
if(E_Detal<0)
{
for(int i=1;i<=n;i++)
{
num[i]=k[i];
}
ans=rans;
}
else if(exp(-E_Detal/t)*RAND_MAX>rand())
{
for(int i=1;i<=n;i++)
{
num[i]=k[i];
}
ans=rans;
}
t*=detal;
}
}
void work()
{
SA();SA();SA();SA();SA();SA();
}
int main()
{
srand(2147483647);
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
num[i]=i;
scanf("%d",&nod[i].a);
scanf("%d",&nod[i].b);
scanf("%d",&nod[i].c);
g[i].push_back(nod[i].a);
g[i].push_back(nod[i].b);
g[i].push_back(nod[i].c);
}
ans=calc(num);
work();
printf("%.0lf",ans);
return 0;
}
【JSOI 2004】平衡点/吊打XXX
模拟退火板子 没啥好说的
AC code
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<algorithm>
#define detal 0.998
using namespace std;
const int maxn=1010;
int n;
struct node
{
double x,y,w;
}nod[maxn];
double sum_x;
double sum_y;
double ans_x;
double ans_y;
double ans_w;
double calc(double x,double y)
{
double ans=0;
for(int i=1;i<=n;i++)
{
double dx=(x-nod[i].x);
double dy=(y-nod[i].y);
ans+=sqrt(dx*dx+dy*dy)*nod[i].w;
}
return ans;
}
void SA()
{
double x=ans_x,y=ans_y;
double t=3000;
while(t>1e-15)
{
double rx=x+(rand()<<1-RAND_MAX)*t;
double ry=y+(rand()<<1-RAND_MAX)*t;
double rw=calc(rx,ry);
double E_Detal=rw-ans_w;
if(E_Detal<0)
{
ans_x=rx,ans_y=ry;
ans_w=rw;x=rx,y=ry;
}
else if(exp(-E_Detal/t)*RAND_MAX>rand())
{
x=rx,y=ry;
ans_x=rx;
ans_y=ry;
}
t*=detal;
}
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%lf",&nod[i].x);
scanf("%lf",&nod[i].y);
scanf("%lf",&nod[i].w);
sum_x+=nod[i].x;
sum_y+=nod[i].y;
}
ans_x=(double)sum_x/n;
ans_y=(double)sum_y/n;
ans_w=calc(ans_x,ans_y);
SA();SA();SA();SA();SA();SA();SA();
printf("%.3lf %.3lf",ans_x,ans_y);
return 0;
}
【SDOI 2014】旅行
一眼树剖,然后发现每次询问时这条路径上只有某一种宗教会产生贡献,然而这并不好维护
然后我就想到了每种宗教开一棵线段树 一看数据范围1e5铁定GG
然后就打开了题解 开篇就是"对于每一个宗教建一个线段树"
?wdnmd 然后就发现可以动态开点 NB啊woc
然后就成了板子题
AC code
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<algorithm>
using namespace std;
const int maxn=1e5+5;
inline int read()
{
int w=0,f=1;
char ch=getchar();
while(ch<'0' || ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9')
{
w=(w<<3)+(w<<1)+(ch^48);
ch=getchar();
}
return w*f;
}
int cnt;
int n,q,tot;
int w[maxn];
int c[maxn];
int head[maxn];
struct edge
{
int to,next,val;
}e[maxn*2];
int max_son[maxn];
int root[maxn],fa[maxn];
int id[maxn],deep[maxn];
int siz[maxn],top[maxn];
struct s_t
{
int cnt;
int mxa;
int ls,rs;
}t[maxn<<5];
void add(int x,int y)
{
e[++tot].to=y;
e[tot].next=head[x];
head[x]=tot;
}
void dfs_first(int x,int f)
{
fa[x]=f;deep[x]=deep[f]+1;siz[x]=1;
for(int i=head[x];i;i=e[i].next)
{
int to=e[i].to;
if(to==f)continue;
dfs_first(to,x);
siz[x]+=siz[to];
if(siz[to]>siz[max_son[x]])
{
max_son[x]=to;
}
}
}
void dfs_second(int x,int t)
{
id[x]=++tot;top[x]=t;
if(!max_son[x]) return ;
dfs_second(max_son[x],top[x]);
for(int i=head[x];i;i=e[i].next)
{
int to=e[i].to;
if(to!=max_son[x] && to!=fa[x])
{
dfs_second(to,to);
}
}
}
void update(int &p,int l,int r,int pos,int k)
{
if(!p) p=++cnt;
t[p].mxa=max(t[p].mxa,k),t[p].cnt+=k;
if(l==r) return ;
int mid=(l+r)>>1;
if(pos<=mid) update(t[p].ls,l,mid,pos,k);
else update(t[p].rs,mid+1,r,pos,k);
}
void del(int &p,int l,int r,int pos)
{
if(l==r) {t[p].cnt=0,t[p].mxa=0;return;}
int mid=(l+r)>>1;
if(pos<=mid) del(t[p].ls,l,mid,pos);
else del(t[p].rs,mid+1,r,pos);
t[p].cnt=t[t[p].ls].cnt+t[t[p].rs].cnt;
t[p].mxa=max(t[t[p].ls].mxa,t[t[p].rs].mxa);
}
int query_sum(int p,int l,int r,int ql,int qr)
{
if(qr<l || ql>r) return 0;
if(ql<=l && r<=qr) return t[p].cnt;
int mid=(l+r)>>1;
int ans=0;
if(ql<=mid) ans+=query_sum(t[p].ls,l,mid,ql,qr);
if(qr>mid) ans+=query_sum(t[p].rs,mid+1,r,ql,qr);
return ans;
}
int query_max(int p,int l,int r,int ql,int qr)
{
if(qr<l || ql>r) return 0;
if(ql<=l && r<=qr) return t[p].mxa;
int mid=(l+r)>>1;
int ans=0;
if(ql<=mid) ans=max(ans,query_max(t[p].ls,l,mid,ql,qr));
if(qr>mid) ans=max(ans,query_max(t[p].rs,mid+1,r,ql,qr));
return ans;
}
int get_sum(int x,int y,int z)
{
int ans=0;
while(top[x]!=top[y])
{
if(deep[top[x]]<deep[top[y]]) swap(x,y);
ans+=query_sum(root[z],1,n,id[top[x]],id[x]);
x=fa[top[x]];
}
if(deep[x]>deep[y]) swap(x,y);
ans+=query_sum(root[z],1,n,id[x],id[y]);
return ans;
}
int get_max(int x,int y,int z)
{
int ans=0;
while(top[x]!=top[y])
{
if(deep[top[x]]<deep[top[y]]) swap(x,y);
ans=max(ans,query_max(root[z],1,n,id[top[x]],id[x]));
x=fa[top[x]];
}
if(deep[x]>deep[y]) swap(x,y);
ans=max(ans,query_max(root[z],1,n,id[x],id[y]));
return ans;
}
int main()
{
n=read(),q=read();
for(int i=1;i<=n;i++)
w[i]=read(),c[i]=read();
for(int i=1;i<n;i++)
{
int u=read();
int v=read();
add(u,v),add(v,u);
}
tot=0,dfs_first(1,0);
tot=0,dfs_second(1,1);
for(int i=1;i<=n;i++)
update(root[c[i]],1,n,id[i],w[i]);
while(q--)
{
char opt[maxn];
scanf("%s",opt);
if(opt[1]=='S')
{
int x=read(),y=read();
cout<<get_sum(x,y,c[x])<<endl;
}
if(opt[1]=='C')
{
int x=read(),k=read();
del(root[c[x]],1,n,id[x]);
update(root[k],1,n,id[x],w[x]);
c[x]=k;
}
if(opt[1]=='W')
{
int x=read(),k=read();
del(root[c[x]],1,n,id[x]);
update(root[c[x]],1,n,id[x],k);
w[x]=k;
}
if(opt[1]=='M')
{
int x=read(),y=read();
cout<<get_max(x,y,c[x])<<endl;
}
}
return 0;
}
Day -1
Distance in Tree
点分治板子题
AC code
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<algorithm>
using namespace std;
const int maxn=5e4+5;
inline int read()
{
int w=0,f=1;
char ch=getchar();
while(ch<'0' || ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9')
{
w=(w<<3)+(w<<1)+(ch^48);
ch=getchar();
}
return w*f;
}
int SIZ,k,ans;
int n,m,tot;
int q[maxn];
int root,cnt;
int head[maxn];
int d[maxn];
struct edge
{
int to,next,val;
}e[maxn*2];
void add(int x,int y)
{
e[++tot].to=y;
e[tot].val=1;
e[tot].next=head[x];
head[x]=tot;
}
bool use[maxn];
int dp[maxn],siz[maxn];
void get_root(int x,int f)
{
siz[x]=1;dp[x]=0;
for(int i=head[x];i;i=e[i].next)
{
int to=e[i].to;
if(use[to] || to==f) continue;
get_root(to,x);
dp[x]=max(dp[x],siz[to]);
siz[x]+=siz[to];
}
dp[x]=max(dp[x],SIZ-siz[x]);
if(dp[x]<dp[root]) root=x;
}
int find_l(int l,int x)
{
int ans=0,r=cnt;
while(l<=r)
{
int mid=(l+r)>>1;
if(d[mid]<x) l=mid+1;
else r=mid-1,ans=mid;
}
return ans;
}
int find_r(int l,int x)
{
int ans=0,r=cnt;
while(l<=r)
{
int mid=(l+r)>>1;
if(d[mid]<=x) ans=mid,l=mid+1;
else r=mid-1;
}
return ans;
}
void get_dis(int x,int f,int d_f)
{
for(int i=head[x];i;i=e[i].next)
{
int to=e[i].to;
if(use[to] || to==f) continue;
d[++cnt]=d_f+e[i].val;
get_dis(to,x,d[cnt]);
}
}
int calc(int x,int dis)
{
d[cnt=1]=dis;
get_dis(x,0,dis);
sort(d+1,d+cnt+1);
int l=1,ans=0;
while(l<cnt && d[l]+d[cnt]<k) l++;
while(l<cnt && k-d[l]>=d[l])
{
int l_ans=find_l(l+1,k-d[l]);
int r_ans=find_r(l+1,k-d[l]);
if(r_ans>=l_ans) ans+=r_ans-l_ans+1;
l++;
}
return ans;
}
void dfs(int x)
{
use[x]=true;ans+=calc(x,0);
for(int i=head[x];i;i=e[i].next)
{
int to=e[i].to;
if(use[to]) continue;
SIZ=siz[to],root=0;
ans-=calc(to,1);
get_root(to,x);
dfs(root);
}
}
int main()
{
n=read(),k=read();
for(int i=1;i<n;i++)
{
int u=read();
int v=read();
add(u,v),add(v,u);
}
SIZ=n;dp[0]=n;
get_root(1,0);
dfs(root);
cout<<ans;
return 0;
}
【TJOI 2010】分金币
模拟退火,先分好两部分,每次随机两部分各一个数互换
AC code
点击查看代码
#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<climits>
#include<cmath>
#include<algorithm>
#define detal 0.996
using namespace std;
const int maxn=35;
inline int read()
{
int w=0,f=1;
char ch=getchar();
while(ch<'0' || ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9')
{
w=(w<<3)+(w<<1)+(ch^48);
ch=getchar();
}
return w*f;
}
double ans;
int sum[maxn];
int t,n,v[maxn];
double calc(int *val)
{
double sum_1=0,sum_2=0;
for(int i=1;i<=(n+1)/2;i++)
{
sum_1+=val[i];
}
for(int i=(n+1)/2+1;i<=n;i++)
{
sum_2+=val[i];
}
return abs(sum_1-sum_2);
}
void SA()
{
double t=3000;
while(t>1e-10)
{
int x=rand()%n+1;
int y=rand()%n+1;
swap(v[x],v[y]);
double rans=calc(v);
double E_Detal=rans-ans;
if(E_Detal<0)
{
ans=rans;
}
else if(exp(-E_Detal/t)*RAND_MAX<rand())
{
swap(v[x],v[y]);
}
t*=detal;
}
}
void work()
{
SA();SA();SA();SA();SA();SA();
}
int main()
{
srand(998244353);
t=read();
while(t--)
{
n=read();
for(int i=1;i<=n;i++)
{
v[i]=read();
}
ans=calc(v);
work();
printf("%.0lf\n",ans);
}
return 0;
}
Run Away
模拟退火
AC code
点击查看代码
#include<iostream>
#include<cstring>
#include<string>
#include<cmath>
#include<algorithm>
#include<ctime>
#include<cstdio>
#include<climits>
#define detal 0.9954321
using namespace std;
const int maxn=1010;
struct node
{
double x,y;
}nod[maxn];
int range_x, range_y, m, sumx, sumy, T;
double ansx, ansy, t, ans, t_delta = 0.995;
double calc(double x, double y)
{
double res = INT_MAX;
for (int i = 1; i <= m; i++)
{
double deltax = x - nod[i].x;
double deltay = y - nod[i].y;
res = min(res, sqrt(deltax * deltax + deltay * deltay));
}
return res;
}
void SA()
{
double x = ansx;
double y = ansy;
t = double(max((double)range_x, (double)range_y)) / sqrt((double)m);
while (t > 1e-5)
{
double angle = double(rand() % 1000 + 1) / 1000.0 * 2.0 * acos(-1.0);
double deltax = t * cos(angle);
double deltay = t * sin(angle);
double X = abs(x + deltax);
double Y = abs(y + deltay);
if (X < 1e-5 || X > range_x || Y < 1e-5 || Y > range_y)
continue;
double energy = calc(X, Y);
double energy_delta = ans - energy;
if (energy_delta < 0)
{
ans = energy;
ansx = x = X;
ansy = y = Y;
}
else if (exp(-energy_delta / t) * RAND_MAX > rand())
{
x = X;
y = Y;
}
t *= t_delta;
}
}
void solve()
{
ansx = double(sumx / m);
ansy = double(sumy / m);
for (int i = 1; i <= 500; i++)
SA();
}
int main()
{
srand(12345678);
srand(rand());
srand(rand());
cin >> T;
while (T)
{
T--;
cin >> range_x >> range_y >> m;
ans = 0;
sumx = 0, sumy = 0;
for (int i = 1; i <= m; i++)
{
cin >> nod[i].x >> nod[i].y;
sumx += nod[i].x;
sumy += nod[i].y;
}
solve();
printf("The safest point is (%.1lf, %.1lf).\n", ansx, ansy);
}
}
Present
看到异或想拆位,单独判断某位是否为1,如果为这位1则分为进位与不进位两种情况
-
不进位则两数之和在\(2^k,2^{k+1}-1\)范围内
-
进位则两数之和在\(2^k+2^{k+1},2^{k+2}-2\)范围内
排序双指针扫一遍即可
AC code
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<algorithm>
using namespace std;
const int maxn=4e5+5;
inline int read()
{
int w=0,f=1;
char ch=getchar();
while(ch<'0' || ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9')
{
w=(w<<3)+(w<<1)+(ch^48);
ch=getchar();
}
return w*f;
}
int n,b[maxn],a[maxn],ans;
bool find(int L,int R)
{
if(L>R) return 0;
int cnt=0,l=1,r=1;
for(int i=n;i;i--)
{
while(l<=n && b[i]+b[l]<L) l++;
while(r<=n && b[i]+b[r]<=R) r++;
cnt+=r-l-(l<=i && i<r);
}
return (cnt>>1)&1;
}
int solve(int k)
{
for(int i=1;i<=n;i++)b[i]=a[i]&((1<<k+1)-1);
sort(b+1,b+n+1);
return find(1<<k,(1<<(k+1))-1)^find(3<<k,(1<<(k+2))-2);
}
int main()
{
n=read();
for(int i=1;i<=n;i++)
{
a[i]=read();
}
for(int i=0;i<=25;i++)
{
ans|=solve(i)<<i;
}
cout<<ans;
return 0;
}
食塩水
二分,分数规划,写了题解
AC code
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<algorithm>
using namespace std;
const int maxn=1010;
const double eps=1e-10;
int n,k;
struct water
{
double p,w,g;
}w[maxn];
bool cmp(water x,water y)
{
return x.g>y.g;
}
bool check(double x)
{
for(int i=1;i<=n;i++) w[i].g=(w[i].p-x)*w[i].w;
sort(w+1,w+n+1,cmp);
double ans=0;
for(int i=1;i<=k;i++)
{
ans+=w[i].g;
}
return ans>=0;
}
int main()
{
cin>>n>>k;
for(int i=1;i<=n;i++)
{
cin>>w[i].w>>w[i].p;
}
double l=0,r=100;
while(r-l>=eps)
{
double mid=(l+r)/2;
if(check(mid)) l=mid;
else r=mid;
}
printf("%.9lf",l);
return 0;
}
【CEOI 2004】锯木厂选址
比较简单的斜率优化,模拟退火也行(不过感觉模拟退火更麻烦所以斜率优化了)
AC code
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<climits>
#include<algorithm>
using namespace std;
const int maxn=20010;
inline int read()
{
int w=0,f=1;
char ch=getchar();
while(ch<'0' || ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9')
{
w=(w<<3)+(w<<1)+(ch^48);
ch=getchar();
}
return w*f;
}
int ans;
int head=1;
int tail=1;
int q[maxn];
int dp[maxn];
int s,d[maxn];
int n,w[maxn];
int sum[maxn];
int dis[maxn];
double x(int i)
{
return sum[i];
}
double y(int i)
{
return dis[i]*sum[i];
}
long double slope(int a,int b)
{
return (long double)(y(a)-y(b))/(x(a)-x(b));
}
int main()
{
n=read(),ans=INT_MAX;
for(int i=1;i<=n;i++)
{
scanf("%d%d",&w[i],&d[i]);
}
for(int i=1;i<=n;i++)
{
sum[i]=sum[i-1]+w[i];
}
for(int i=n;i>=1;i--)
{
dis[i]=dis[i+1]+d[i];
s+=w[i]*dis[i];
}
for(int i=1;i<=n;i++)
{
while(head<tail && slope(q[head],q[head+1])>dis[i])
{
head++;
}
ans=min(ans,s-dis[q[head]]*sum[q[head]]-dis[i]*(sum[i]-sum[q[head]]));
while(head<tail && slope(q[tail-1],q[tail])<slope(q[tail],i)) tail--;
q[++tail]=i;
}
printf("%d",ans);
return 0;
}
【CEOI 2016】kangaroo
比较套路的DP,学名排列DP,这类DP主要是维护成块,先转变为从小到大插入数字,会得到M形,然后分类讨论是新建一个块还是合并两个块即可
注意s和t的限制
AC code
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<algorithm>
#define int long long
using namespace std;
const int mod=1e9+7;
int n,s,t,dp[2010][2010];
signed main()
{
scanf("%d%d%d",&n,&s,&t);
dp[1][1]=1;
for(int i=2;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(i==s || i==t)
{
dp[i][j]+=dp[i-1][j-1]+dp[i-1][j];
dp[i][j]%=mod;
continue;
}
int res=(i>s)+(i>t);
dp[i][j]+=dp[i-1][j-1]*(j-res);
dp[i][j]+=dp[i-1][j+1]*j;
dp[i][j]%=mod;
}
}
cout<<dp[n][1]<<endl;
return 0;
}
One Occurrence
刷DP头疼了,刷了道DS水题 莫队会被卡常,最后考虑值域分块,这样可以减小移动指针的次数,减小常数
然后T了
把输出的endl换成\n
A了
加上wljss的火车头+武煦IO+C++20+O2
用莫队拿到最优解第九(前八都是主席树),而且跑得比某些主席树快了将近1000ms
AC code
点击查看代码
#pragma GCC diagnostic error "-std=c++14"
#pragma GCC target("avx")
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#pragma GCC optimize("inline")
#pragma GCC optimize("-fgcse")
#pragma GCC optimize("-fgcse-lm")
#pragma GCC optimize("-fipa-sra")
#pragma GCC optimize("-ftree-pre")
#pragma GCC optimize("-ftree-vrp")
#pragma GCC optimize("-fpeephole2")
#pragma GCC optimize("-ffast-math")
#pragma GCC optimize("-fsched-spec")
#pragma GCC optimize("unroll-loops")
#pragma GCC optimize("-falign-jumps")
#pragma GCC optimize("-falign-loops")
#pragma GCC optimize("-falign-labels")
#pragma GCC optimize("-fdevirtualize")
#pragma GCC optimize("-fcaller-saves")
#pragma GCC optimize("-fcrossjumping")
#pragma GCC optimize("-fthread-jumps")
#pragma GCC optimize("-funroll-loops")
#pragma GCC optimize("-fwhole-program")
#pragma GCC optimize("-freorder-blocks")
#pragma GCC optimize("-fschedule-insns")
#pragma GCC optimize("inline-functions")
#pragma GCC optimize("-ftree-tail-merge")
#pragma GCC optimize("-fschedule-insns2")
#pragma GCC optimize("-fstrict-aliasing")
#pragma GCC optimize("-fstrict-overflow")
#pragma GCC optimize("-falign-functions")
#pragma GCC optimize("-fcse-skip-blocks")
#pragma GCC optimize("-fcse-follow-jumps")
#pragma GCC optimize("-fsched-interblock")
#pragma GCC optimize("-fpartial-inlining")
#pragma GCC optimize("no-stack-protector")
#pragma GCC optimize("-freorder-functions")
#pragma GCC optimize("-findirect-inlining")
#pragma GCC optimize("-fhoist-adjacent-loads")
#pragma GCC optimize("-frerun-cse-after-loop")
#pragma GCC optimize("inline-small-functions")
#pragma GCC optimize("-finline-small-functions")
#pragma GCC optimize("-ftree-switch-conversion")
#pragma GCC optimize("-foptimize-sibling-calls")
#pragma GCC optimize("-fexpensive-optimizations")
#pragma GCC optimize("-funsafe-loop-optimizations")
#pragma GCC optimize("inline-functions-called-once")
#pragma GCC optimize("-fdelete-null-pointer-checks")
#include<iostream>
#include<cstring>
#include<string>
#include<algorithm>
#include<cmath>
using namespace std;
const int maxn=5e5+5;
namespace Octane {
// non terrae plus ultra
#define OCTANE
#define BUFFER_SIZE 100000
#define ll long long
#define db double
#define ldb long double
char ibuf[BUFFER_SIZE], obuf[BUFFER_SIZE];
char *p1 = ibuf, *p2 = ibuf, *p3 = obuf;
#ifdef ONLINE_JUDGE
#define getchar() ((p1==p2)and(p2=(p1=ibuf)+fread(ibuf,1,BUFFER_SIZE,stdin),p1==p2)?(EOF):(*p1++))
#define putchar(x) ((p3==obuf+BUFFER_SIZE)&&(fwrite(obuf,p3-obuf,1,stdout),p3=obuf),*p3++=x)
#endif // fread in OJ, getchar in local
#define isdigit(ch) (ch>47&&ch<58)
#define isspace(ch) (ch<33&&ch!=EOF)
const ll pow10[] = {
(ll)1e0, (ll)1e1, (ll)1e2, (ll)1e3, (ll)1e4, (ll)1e5,
(ll)1e6, (ll)1e7, (ll)1e8, (ll)1e9, (ll)1e10, (ll)1e11,
(ll)1e12, (ll)1e13, (ll)1e14, (ll)1e15, (ll)1e16, (ll)1e17, (ll)1e18,
};
struct Octane_t {
~Octane_t() {
fwrite(obuf, p3-obuf, 1, stdout);
}
bool flag = false;
operator bool() {
return flag;
}
}io;
template<typename T> inline T read() {
T s = 0; int w = 1; char ch;
while(ch=getchar(), !isdigit(ch)&&(ch!=EOF))
if(ch == '-') w = -1;
if(ch == EOF) return 0;
while(isdigit(ch))
s = s*10+ch-48, ch=getchar();
if(ch == '.') {
ll flt = 0; int cnt = 0;
while(ch=getchar(), isdigit(ch))
if(cnt < 18) flt=flt*10+ch-48, cnt++;
s += (db)flt/pow10[cnt];
}
return s *= w;
}
template<typename T> inline bool read(T &s) {
s = 0; int w = 1; char ch;
while(ch=getchar(), !isdigit(ch)&&(ch!=EOF))
if(ch == '-') w = -1;
if(ch == EOF) return false;
while(isdigit(ch))
s = s*10+ch-48, ch=getchar();
if(ch == '.') {
ll flt = 0; int cnt = 0;
while(ch=getchar(), isdigit(ch))
if(cnt < 18) flt=flt*10+ch-48, cnt++;
s += (db)flt/pow10[cnt];
}
return s *= w, true;
}
inline bool read(char &s) {
while(s = getchar(), isspace(s));
return s != EOF;
}
inline bool read(char *s) {
char ch;
while(ch=getchar(), isspace(ch));
if(ch == EOF) return false;
while(!isspace(ch))
*s++ = ch, ch=getchar();
*s = '\000';
return true;
}
template<typename T> void print(T x) {
static int t[20]; int top = 0;
if(x < 0) putchar('-'), x = -x;
do { t[++top] = x%10; x /= 10; } while(x);
while(top) putchar(t[top--]+48);
}
struct empty_type{}; int pcs = 8;
empty_type setpcs(int cnt) {
return pcs = cnt, empty_type();
}
inline void print(empty_type x){}
inline void print(double x) {
if(x < 0) putchar('-'), x = -x;
x += 5.0 / pow10[pcs+1];
print((ll)(x)); x -= (ll)(x);
if(pcs != 0) putchar('.');
for(int i = 1; i <= pcs; i++)
x *= 10, putchar((int)x+'0'), x -= (int)x;
}
inline void print(float x) {
if(x < 0) putchar('-'), x = -x;
x += 5.0 / pow10[pcs+1];
print((ll)(x)); x -= (ll)(x);
if(pcs != 0) putchar('.');
for(int i = 1; i <= pcs; i++)
x *= 10, putchar((int)x+'0'), x -= (int)x;
}
inline void print(char x) {
putchar(x);
}
inline void print(char *x) {
for(int i = 0; x[i]; i++)
putchar(x[i]);
}
inline void print(const char *x) {
for(int i = 0; x[i]; i++)
putchar(x[i]);
}
// support for string
#ifdef _GLIBCXX_STRING
inline bool read(std::string& s) {
s = ""; char ch;
while(ch=getchar(), isspace(ch));
if(ch == EOF) return false;
while(!isspace(ch))
s += ch, ch = getchar();
return true;
}
inline void print(std::string x) {
for(string::iterator i = x.begin(); i != x.end(); i++)
putchar(*i);
}
inline bool getline(Octane_t &io, string s) {
s = ""; char ch = getchar();
if(ch == EOF) return false;
while(ch != '\n' and ch != EOF)
s += ch, ch = getchar();
return true;
}
#endif
// support for initializer_list
#if __cplusplus >= 201103L
template<typename T, typename... T1>
inline int read(T& a, T1& ...other) {
return read(a)+read(other...);
}
template<typename T, typename... T1>
inline void print(T a, T1... other) {
print(a); print(other...);
}
#endif
// give up iostream
template<typename T>
Octane_t& operator >> (Octane_t &io, T &b) {
return io.flag=read(b), io;
}
Octane_t& operator >> (Octane_t &io, char *b) {
return io.flag=read(b), io;
}
template<typename T>
Octane_t& operator << (Octane_t &io, T b) {
return print(b), io;
}
#define cout io
#define cin io
#define endl '\n'
#undef ll
#undef db
#undef ldb
#undef BUFFER_SIZE
}
using namespace Octane;
int n,m;
int num,siz;
int en[5010];
int ans[maxn];
int sum[maxn];
int cnt[maxn];
int val[maxn];
int bel[maxn];
struct que
{
int l,r;
int id,ans;
}q[maxn];
bool cmp(que x,que y)
{
return bel[x.l]!=bel[y.l] ? bel[x.l]<bel[y.l] : (bel[x.l] & 1 ? x.r<y.r : x.r>y.r);
}
void add(int x)
{
if(cnt[val[x]]==1)sum[bel[val[x]]]--;
if(cnt[val[x]]==0)sum[bel[val[x]]]++;
cnt[val[x]]++;
}
void del(int x)
{
if(cnt[val[x]]==1)sum[bel[val[x]]]--;
if(cnt[val[x]]==2)sum[bel[val[x]]]++;
cnt[val[x]]--;
}
int query()
{
for(int i=bel[n];i;i--)
{
if(!sum[i])continue;
for(int j=en[i];bel[j]==i;j--)
{
if(cnt[j]==1) return j;
}
}
return 0;
}
int main()
{
read(n);
siz=sqrt(n);
num=ceil((double)n/siz);
for(int i=1;i<=num;i++)
{
for(int j=(i-1)*siz+1;j<=min(siz*i,n);j++)
{
bel[j]=i;
en[bel[j]]=j;
}
}
for(int i=1;i<=n;i++)
read(val[i]);
read(m);
for(int i=1;i<=m;i++)
{
q[i].id=i;
read(q[i].l);
read(q[i].r);
}
sort(q+1,q+m+1,cmp);
int l=1,r=0;
for(int i=1;i<=m;i++)
{
while(l<q[i].l) del(l++);
while(l>q[i].l) add(--l);
while(r<q[i].r) add(++r);
while(r>q[i].r) del(r--);
ans[q[i].id]=query();
}
for(int i=1;i<=m;i++)
{
cout<<ans[i]<<'\n';
}
return 0;
}

 CSP-S 2022 RP++
CSP-S 2022 RP++

 浙公网安备 33010602011771号
浙公网安备 33010602011771号