BZOJ 4085 丧心病狂的毒瘤题目 线段树+矩乘
思路:
一眼矩阵快速幂 再用线段树维护一下矩阵就完了...
我hhhhh 哎我还是too young,too simple 入了这个大坑
线段树维护9个值

以上
如果A+1 转移矩阵是这个样子的

B+1
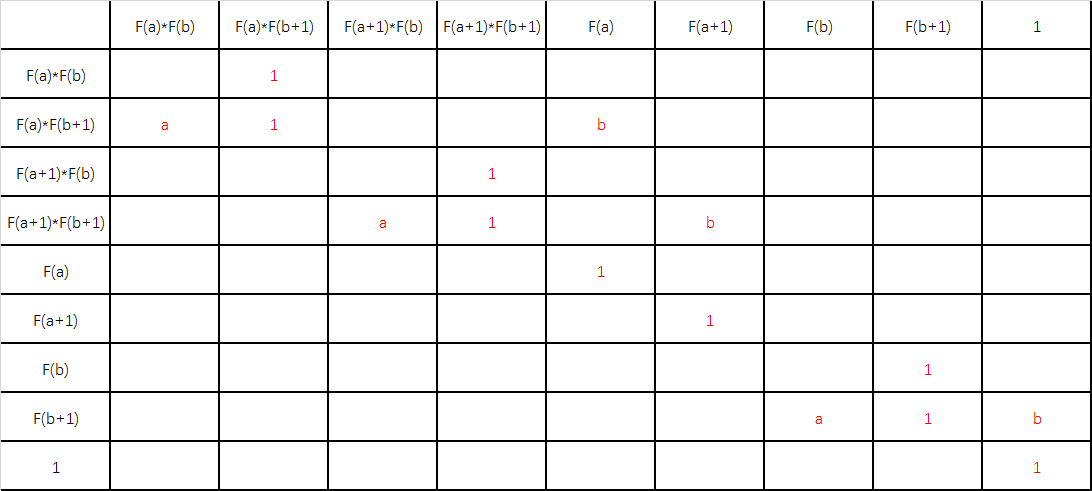
A-1 B-1 同理行么.....
写了一晚上+一上午 调完了
发现自己被卡常?
我了个大曹
我们发现一开始的矩阵最后一行不变
矩乘的时候特判一发 还是过不去
预处理2^k的矩阵
快速幂的时候省一倍常数 加个快读
80432 ms
卡过去了!!
//By SiriusRen #include <bits/stdc++.h> using namespace std; const int mod=1000000007,N=300005; int n,q,a,b,A[N],F[N],d[N][4],lazy[N*8][2]; inline int read(){ int x=0;char p=getchar(); while(p<'0'||p>'9')p=getchar(); while(p>='0'&&p<='9')x=x*10+p-'0',p=getchar(); return x; } struct MATRIX{ int a[3][3]; void init(){memset(a,0,sizeof(a));} }t[32],t0; int pow(int x,int y){ int res=1; while(y){ if(y&1)res=1ll*res*x%mod; x=1ll*x*x%mod,y>>=1; }return res; } MATRIX operator*(MATRIX &a,MATRIX &b){ static MATRIX c;c.init(); for(int i=0;i<2;i++) for(int j=0;j<3;j++){ for(int k=0;k<3;k++) c.a[i][j]=(c.a[i][j]+1ll*a.a[i][k]*b.a[k][j])%mod; } c.a[2][2]=1; return c; } MATRIX power(int k){ static MATRIX res;res.init(); res.a[0][0]=res.a[1][1]=res.a[2][2]=1; for(int i=1;k;k>>=1,i++)if(k&1)res=res*t[i]; return res; } struct Matrix{ int m[9][9]; void init(){memset(m,0,sizeof(m));} void init1(){ int B[9][9]={ {0,0,1,0,0,0,0,0,0}, {0,0,0,1,0,0,0,0,0}, {a,0,1,0,0,0,b,0,0}, {0,a,0,1,0,0,0,b,0}, {0,0,0,0,0,1,0,0,0}, {0,0,0,0,a,1,0,0,b}, {0,0,0,0,0,0,1,0,0}, {0,0,0,0,0,0,0,1,0}, {0,0,0,0,0,0,0,0,1}, }; memcpy(m,B,sizeof(B)); } void init2(){ int B[9][9]={ {0,1,0,0,0,0,0,0,0}, {a,1,0,0,b,0,0,0,0}, {0,0,0,1,0,0,0,0,0}, {0,0,a,1,0,b,0,0,0}, {0,0,0,0,1,0,0,0,0}, {0,0,0,0,0,1,0,0,0}, {0,0,0,0,0,0,0,1,0}, {0,0,0,0,0,0,a,1,b}, {0,0,0,0,0,0,0,0,1}, }; memcpy(m,B,sizeof(B)); } void init3(){ int x,y,z; if(a){ int inv=pow(a,mod-2); x=inv,y=mod-inv,z=1ll*b*(mod-inv)%mod; } else x=0,y=1,z=mod-b; int B[9][9]={ {y,0,x,0,0,0,z,0,0}, {0,y,0,x,0,0,0,z,0}, {1,0,0,0,0,0,0,0,0}, {0,1,0,0,0,0,0,0,0}, {0,0,0,0,y,x,0,0,z}, {0,0,0,0,1,0,0,0,0}, {0,0,0,0,0,0,1,0,0}, {0,0,0,0,0,0,0,1,0}, {0,0,0,0,0,0,0,0,1}, }; memcpy(m,B,sizeof(B)); } void init4(){ int x,y,z; if(a){ int inv=pow(a,mod-2); x=inv,y=mod-inv,z=1ll*b*(mod-inv)%mod; } else x=0,y=1,z=mod-b; int B[9][9]={ {y,x,0,0,z,0,0,0,0}, {1,0,0,0,0,0,0,0,0}, {0,0,y,x,0,z,0,0,0}, {0,0,1,0,0,0,0,0,0}, {0,0,0,0,1,0,0,0,0}, {0,0,0,0,0,1,0,0,0}, {0,0,0,0,0,0,y,x,z}, {0,0,0,0,0,0,1,0,0}, {0,0,0,0,0,0,0,0,1}, }; memcpy(m,B,sizeof(B)); } }cng[4][14],I; Matrix operator*(Matrix &a,Matrix &b){ Matrix c;c.init(); for(int i=0;i<9;i++) for(int j=0;j<9;j++){ for(int k=0;k<9;k++) c.m[i][j]=(c.m[i][j]+1ll*a.m[i][k]*b.m[k][j])%mod; } return c; } void bz(){ cng[0][1].init1();cng[1][1].init2(); cng[2][1].init3();cng[3][1].init4(); for(int i=0;i<4;i++){ cng[i][0]=I; for(int j=2;j<=13;j++) cng[i][j]=cng[i][j-1]*cng[i][j-1]; } } struct Line{ int m[9]; void set(int aa_1,int aa,int bb_1,int bb){ m[0]=1ll*aa_1*bb_1%mod,m[1]=1ll*aa_1*bb%mod,m[2]=1ll*aa*bb_1%mod, m[3]=1ll*aa*bb%mod,m[4]=aa_1,m[5]=aa,m[6]=bb_1,m[7]=bb,m[8]=1; } }tr[1<<20],ans; Line operator+(Line &a,Line &b){ Line c; for(int i=0;i<9;i++)c.m[i]=(a.m[i]+b.m[i])%mod; return c; } Line operator*(Matrix &a,Line &b){ Line c;memset(c.m,0,sizeof(c.m)); for(int i=0;i<9;i++) for(int j=0;j<9;j++) c.m[i]=(c.m[i]+1ll*a.m[i][j]*b.m[j])%mod; return c; } void change(Line &f,Matrix r[],int k){ for(int i=1;k;k>>=1,i++)if(k&1)f=r[i]*f; } void calc(int pos,int a0,int a1){ if(a0){ if(a0<0)change(tr[pos],cng[2],-a0); else change(tr[pos],cng[0],a0); } if(a1){ if(a1<0)change(tr[pos],cng[3],-a1); else change(tr[pos],cng[1],a1); } } void push_down(int pos,int l,int r){ calc(pos,lazy[pos][0],lazy[pos][1]); if(l<r){ int lson=pos<<1,rson=pos<<1|1; lazy[lson][0]+=lazy[pos][0],lazy[lson][1]+=lazy[pos][1]; lazy[rson][0]+=lazy[pos][0],lazy[rson][1]+=lazy[pos][1]; } lazy[pos][0]=lazy[pos][1]=0; } void push_up(int pos,int l,int r){ int mid=(l+r)>>1,lson=pos<<1,rson=pos<<1|1; push_down(lson,l,mid),push_down(rson,mid+1,r); tr[pos]=tr[lson]+tr[rson]; } void build(int l,int r,int pos){ if(l==r){ tr[pos].set(d[l-1][2],d[l-1][3],d[r+1][0],d[r+1][1]); return; } int mid=(l+r)>>1,lson=pos<<1,rson=pos<<1|1; build(l,mid,lson),build(mid+1,r,rson); push_up(pos,l,r); } void insert(int l,int r,int pos,int L,int R,int op){ if(L>R)return; if(l>=L&&r<=R){ if(!op)lazy[pos][0]++; else if(op==1)lazy[pos][1]++; else if(op==2)lazy[pos][0]--; else if(op==3)lazy[pos][1]--; return; }push_down(pos,l,r); int mid=(l+r)>>1,lson=pos<<1,rson=pos<<1|1; if(mid<L)insert(mid+1,r,rson,L,R,op); else if(mid>=R)insert(l,mid,lson,L,R,op); else insert(l,mid,lson,L,R,op),insert(mid+1,r,rson,L,R,op); push_up(pos,l,r); } void query(int l,int r,int pos,int L,int R){ if(L>R)return; push_down(pos,l,r); if(l>=L&&r<=R){ans=ans+tr[pos];return;} int mid=(l+r)>>1,lson=pos<<1,rson=pos<<1|1; if(mid<L)query(mid+1,r,rson,L,R); else if(mid>=R)query(l,mid,lson,L,R); else query(l,mid,lson,L,R),query(mid+1,r,rson,L,R); } signed main(){ scanf("%d%d%d%d",&n,&q,&a,&b); for(int i=0;i<9;i++)I.m[i][i]=1; t[1].a[0][0]=t[1].a[1][0]=t[1].a[2][2]=1,t[1].a[0][1]=a,t[1].a[0][2]=b; t0.a[1][0]=t0.a[2][0]=1,t0.a[0][0]=2; for(int i=2;i<=31;i++)t[i]=t[i-1]*t[i-1]; for(int i=1;i<=n;i++){ A[i]=read(); if(A[i]!=1){ MATRIX temp=power(A[i]-2);temp=temp*t0; d[i][0]=temp.a[1][0],d[i][1]=temp.a[0][0]; } else d[i][0]=1,d[i][1]=2; d[i][2]=(d[i][1]+1ll*d[i][0]*a+b)%mod; d[i][3]=(d[i][2]+1ll*d[i][1]*a+b)%mod; }bz(),build(2,n-1,1); while(q--){ char op[10];int l,r; scanf("%s%d%d",op,&l,&r); if(op[0]=='q'){ memset(ans.m,0,sizeof(ans.m)); query(2,n-1,1,l+1,r-1); printf("%d\n",ans.m[0]); } else if(op[0]=='p')insert(2,n-1,1,l+1,min(n-1,r+1),0),insert(2,n-1,1,max(l-1,2),r-1,1); else insert(2,n-1,1,l+1,min(n-1,r+1),2),insert(2,n-1,1,max(l-1,2),r-1,3); } }



