支持向量机
1. SVM描述
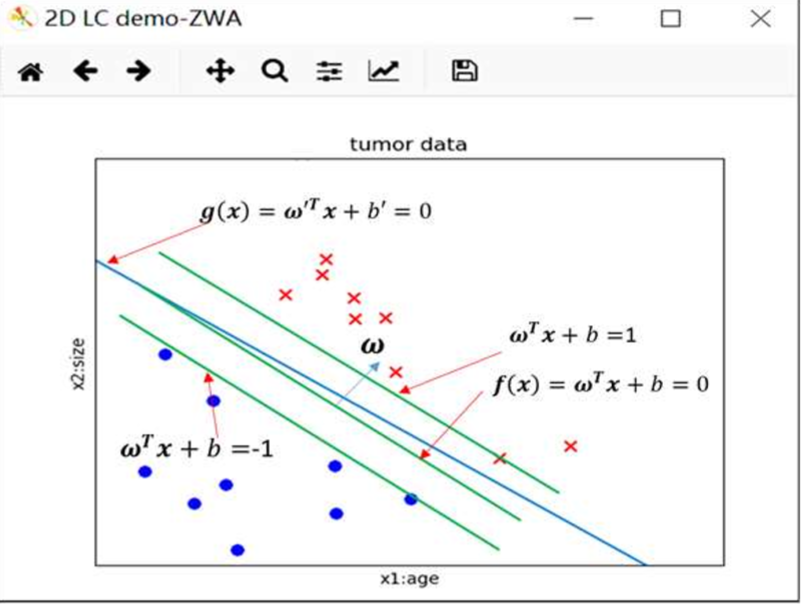
$f(x)$满足间隔最大化要求。与$f(x)$相对应的直线$\omega^Tx+b=-1$和$\omega^Tx+b=1$之间的间隔为$\frac{2}{||\omega||}$。显然,只有直线$\omega^Tx+b=-1$和$\omega^Tx+b=1$上分布的样本点对选取决策面(此时为一直线)有帮助,因此这些点对应的向量称之为支持向量(support vector)。对应最大化间隔模型称为支持向量机(SVM:Support Vector Machine)
SVM问题描述如下:
\begin{cases} \min_{\omega,b}\frac{1}{2}\omega^T\omega&\text{最大化间隔}\\ s.t. y^{(n)}(\omega^Tx^{(n)}+b) \geq 1&n=1,2...N & \text{对所有点有效} \end{cases}
其中$y_i=\pm1$,代表两类不同的点。
2. 拉格朗日乘子法

2.1 等式约束的优化问题
以两个变量为例:
求函数$z=f(x,y)$在满足$\varphi(x,y)=0$条件下的极值,可以转化为函数$F(x,y,\lambda)=f(x,y)+\lambda\varphi(x,y)$的无条件极值问题,其中λ为参数。
令$F(x,y,\lambda)$对$x$和$y$和$\lambda$的一阶偏导数等于零,即
$$F'_x=ƒ'_x(x,y)+\lambda\varphi'_x(x,y)=0$$
$$F'_y=ƒ'_y(x,y)+\lambda\varphi'_y(x,y)=0$$
$$F'_{\lambda}=\varphi(x,y)=0$$
由上述方程组解出$x$,$y$及$\lambda$,如此求得的$(x,y)$,就是函数$z=ƒ(x,y)$在条件$\varphi(x,y)=0$下的可能极值点。
d个变量同理
2.2 不等式约束的优化问题
\begin{aligned} &min&&f(X)\\ &s.t.&&\begin{cases}h_j(X)=0&j=1,2,...p\\g_k(X)\leq0&k=1,2,...q\end{cases}\end{aligned}
定义不等式约束下的拉格朗日函数
$$L(X,\lambda,\mu)=f(X)+\sum_{j=1}^p\lambda_jh_j(X)+\sum_{k=1}^q\mu_kg_k(X)$$
满足 KKT 条件后极小化 Lagrangian 即可得到在不等式约束条件下的可行解:
\begin{cases}\nabla_XL=0\\h_j(X)=0\\g_k(X)\leq0\\\mu_k\geq 0\\ \mu_kg_k(X)=0\end{cases}
2.3 SVM的拉格朗日函数
回顾SVM公式:
\begin{cases} \min_{\omega,b}\frac{1}{2}\omega^T\omega&\text{最大化间隔}\\ s.t. y^{(n)}(\omega^Tx^{(n)}+b) \geq 1&n=1,2...N & \text{对所有点有效} \end{cases}
代入不等式约束的优化问题:
\begin{aligned}\\&f(\omega,b)=\frac{1}{2}||\omega||^2\\&h(\omega,b)=0\\&g(\omega,b)=1-y^{(n)}(\omega^Tx^{(n)}+b)&n=1,2...N\end{aligned}
则:
$$L(\omega,b,\alpha)=\frac{1}{2}||\omega||^2+\sum_{i=1}^N\alpha_i(1-y_i(\omega^Tx_i+b))$$
其中$\alpha_i$为拉格朗日乘子,且$\alpha_i\geq0$
3. 拉格朗日对偶问题
3.1 拉格朗日
广义拉格朗日函数:
$$L(X,\lambda,\mu)=f(X)+\sum_{j=1}^p\lambda_jh_j(X)+\sum_{k=1}^q\mu_kg_k(X)$$
考虑如下式子:
$$\theta_P(X)= \max_{\mu,\lambda; \mu_k\geq0}L(X,\lambda,\mu) $$
其中“P”是“primal(最初问题)”的意思
$$\theta_P(X)=\begin{cases}f(X)&如果X满足最初限定条件\\\infty&否则\end{cases}$$
$\theta_P(X)$的值等于满足最初限定条件$(g(X)\leq0 h(x)=0)$时f(X)的值,问题转化为求使$\theta_P(X)$最小的各变量,此问题定义为$p^*$:
$$p^*=\min_{X}\max_{\mu,\lambda; \mu_k\geq0}L(X,\lambda,\mu)$$
3.2 对偶优化问题
$$\theta_D(\lambda,\mu)=\min_{X}L(X,\lambda,\mu)$$
其中D是“dual(对偶)”的意思,$\theta_D(X)$是基于$X$求极小值,而$\theta_P(X)$是基于$\lambda$和$\mu$求极大值,则对偶优化问题定义为$d^*$如下:
$$d^*=\max_{\mu,\lambda; \mu_k \geq0}\min_{X}L(X,\lambda,\mu)$$
如果我们能够想办法证明(3.14)和(3.13)存在相同的解$X^*,\lambda^*,\mu^*$,那我们就可以在对偶问题中选择比较简单的一个来求解。
3.3对偶问题同解的证明
定理一:对于任意$X,\lambda,\mu$,有$d^*\leq p^*$
$$\theta_D(\lambda,\mu)=\min_{X}L(X,\lambda,\mu)\leq L(X,\lambda,\mu)\leq\max_{\mu,\lambda; \mu_k\geq 0}L(X,\lambda,\mu)=\theta_P(X)$$
故$d^*\leq p^*$
推论:如果能够找到一组$X^*,\lambda^*,\mu^*$使得$\theta_D(\lambda^*,\mu^*)=\theta_P(X^*)$,则有:
$\theta_D(\lambda^*,\mu^*)=d^*$、$\theta_P(X^*)=p^*$、$d^*=p^*$
这个推论实际上已经涉及了原始问题与对偶问题的“强对偶性”。
当$d^*\leq p^*$时,我们称原始问题与对偶问题之间“弱对偶性”成立;若$d^*=p^*$,则称“强对偶性”成立。
定理二:对于原始问题和对偶问题,假设函数$f(x)$和不等式约束条件$g(x)$为凸函数,等式约束条件中的$h(x)$为仿射函数(即由一阶多项式构成的函数);并且至少存在一个$X$使所有不等式约束条件严格成立,则存在$X^*,\lambda^*,\mu^*$使得$X^*$是原始问题的最优解,$\lambda^*,\mu^*$是对偶问题的最优解且有:$d^*=p^*=L(X,\lambda,\mu)$
在强对偶性成立时,将拉格朗日函数分别对元变量和对偶变量求导,再同时令导数等于0,即可得到原变量与对偶变量的数值关系。
于是对偶问题解决了,主问题也就解决了。
3.4 SVM的对偶问题求解
回顾SVM的拉格朗日函数
$$L(\omega,b,\alpha)=\frac{1}{2}||\omega||^2+\sum_{i=1}^N\alpha_i(1-y_i(\omega^Tx_i+b))$$
发现满足强对偶性
分别对$\omega$和$b$求偏导,有偏导为0,可得:
\begin{aligned}\omega&=\sum_{i=1}^N\alpha_iy_ix_i\\0&=\sum_{i=1}^N\alpha_iy_i\end{aligned}
将以上两式带回$L(\omega,b,\alpha)$,化简得:
$$\max[L(\omega,b,\alpha)=\sum_{i=1}^N\alpha_i-\frac{1}{2}\sum_{i,j=1}^N\alpha_i\alpha_jx_i^Tx_jy_iy_j]$$
$s.t.\sum_{i=1}^N\alpha_iy_i=0且\alpha_i\geq0$
此时为一个完全的凸二次规划问题,可以用各种软件包求解(但是很慢),一般用SMO算法求解。
4. SMO优化方法
算法流程:
- 选取一对参数$(\alpha_i,\alpha_j)$
- 固定$\alpha$向量的其他参数,将$\alpha_i,\alpha_j$代入KKT和约束表达式进行求最优解获得更新后的$\alpha_i,\alpha_j$
不断执行这两个步骤直至收敛
因为有约束$\sum_{i=1}^N\alpha_iy_i$存在,有$\alpha_iy_i+\alpha_jy_j=C$(C为常数)
那么我们如何选取α呢?我们怎么知道哪一个α需要优化呢?
我们只要选择违反KKT条件的点,使其符合KKT条件,那么就自然而然可以得到更优解。优化的α违背KKT条件越大,此次优化效果越明显。
所以第一个要选择的α是违反KKT条件的点,而第二个α是与第一个点距离最大的点,因为我们发现一次更新两个不同向量比相似向量的效果好。
收敛后,我们就可以得到所有的α的值。把所有α代进去,就可以得到w的解,接着可以得到b的解。
5. 松弛变量与软间隔
硬间隔支持向量机要求所有的样本均被最佳超平面正确划分,而软间隔支持向量机允许某些样本点不满足间隔大于等于1的条件。当然在最大化间隔的时候也要限制不满足间隔大于等于1的样本的个数使之尽可能的少。于是我们引入一个惩罚系数C,并对每个样本点引入一个松弛变量$\xi_i$
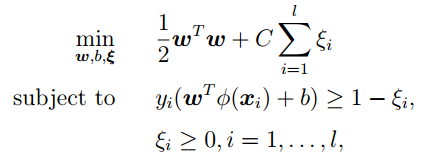
通过计算,我们的优化目标依然保持不变,但是新的约束条件变为

参考文献:
https://zhuanlan.zhihu.com/p/35755150
https://zhuanlan.zhihu.com/p/24638007
https://zhuanlan.zhihu.com/p/57648645
https://blog.csdn.net/qq_39482438/article/details/106908049




