fisher线性分类器
- Fisher准则函数
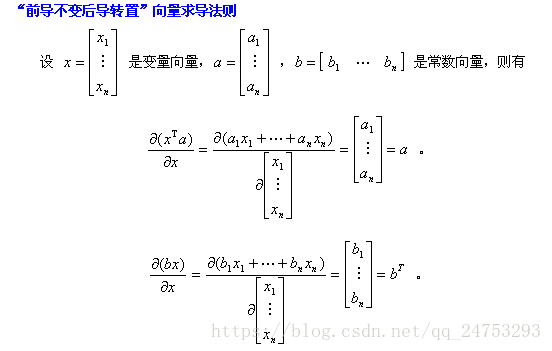
Fisher准则的基本原理:找到一个最合适的投影轴,使两类样本在该轴上投影之间的距离尽可能远,而每一类样本的投影尽可能紧凑,从而使分类效果为最佳。
假设有两类样本,分别为$X_1$和$X_2$
则各类在d维特征空间里的样本均值为:
$$M_i = \frac{1}{n_i}\sum_{x_k\in X_i}x_k \ \ \ i=1,2$$
通过$\omega$变换后,将d维空间里的样本投影到一维。($y_k$是$x_k$通过$\omega$变换后的标量)
各类在1维特征空间里的样本均值为:
$$m_i=\frac{1}{n_i}\sum_{y_k \in Y_i}y_k\ \ \ i=1,2$$
各类样本类内离散度:
$$s_i^2=\sum_{y_k \in Y_i}(y_k-m_i)^2\ \ \ i=1,2$$
我们的目标是变换以后两类样本均值距离尽可能远并且每个样本尽可能聚在一起,即:
$$max J_F(\omega) = \frac{(m_1-m_2)^2}{s_1^2+s_2^2}$$
使$J_F$最大的$\omega*$是最佳解向量,也就是Fisher的线性判别式
- Fisher准则函数的求解
$$y=\omega^Tx$$
$$m_i=\frac{1}{n_i}\sum_{x_k \in X_i}\omega^Tx_k=\omega^TM_i$$
$$(m_1-m_2)^2 = (\omega^TM_1-\omega^TM_2)^2$$
$$= \omega^T(M_1-M_2)(M_1-M_2)^T\omega = \omega^TS_b\omega$$
原始维度下的类间离散度$S_b=(M_1-M_2)(M_1-M_2)^T$
$S_b$表示两类均值向量之间的离散度大小
$$s_1^2+s_2^2=\sum_{x_k \in X_i}(\omega^Tx_k-\omega^TM_i)^2 \ \ \ i=1,2$$
$$=\omega^T · \sum_{x_k \in X_i}(x_k-M_i)(x_k-M_i)^T ·\omega = \omega^TS_w\omega$$
样本"类内总离散度"矩阵$S_w= \sum_{x_k \in X_i}(x_k-M_i)(x_k-M_i)^T \ \ \ i=1,2$
将上述推导结论代入$J_F(\omega)$,得:$J_F(\omega)=\frac{\omega^TS_b\omega}{\omega^TS_w\omega}$
其中$S_b$和$S_w$都可以从样本集$X_i$直接计算出来
用lagrange乘子法求解。令分母为常数$c=\omega^TS_w\omega\ \ \ c\neq0$
$$L(\omega,\lambda)=\omega^TS_b\omega-\lambda(\omega^TS_w\omega-c)$$
$$\frac{\partial L(\omega,\lambda)}{\partial\omega}=2(S_b\omega-\lambda S_w\omega)=0$$
$\omega$是法向量, 所以比例因子可以去掉。
即$\omega = S_w^{-1}(M_1-M-2)$
阈值可以根据选择:
$$b=-\frac{1}{2}(m_1+m_2)=-\frac{1}{2}(\omega^TM_1+\omega^Tm_2)$$
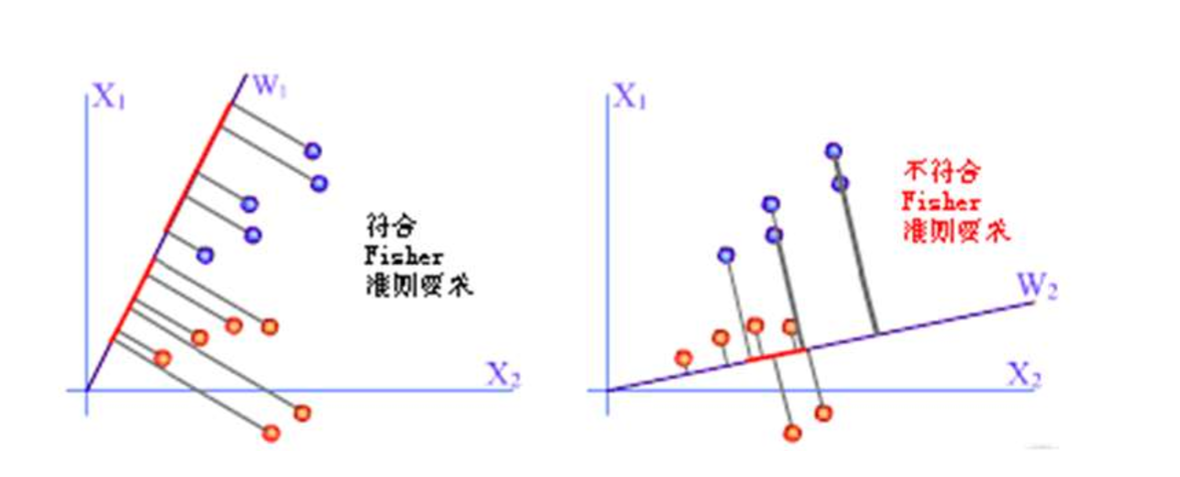
参考代码:
import matplotlib.pyplot as plt import numpy as np import random import math fig=plt.figure()#初始化figure对象 ax=fig.add_subplot(111)#添加子图 ax.set(xlim=[0,100],ylim=[0,100],title='Fisher criterion function') x1=np.zeros((2,100)) x2=np.zeros((2,100))#新建2*100的矩阵用来保存数据 for i in range(100):#随机生成第1类点 rd=random.uniform(0,25)#随机向量长度 rd2=random.uniform(-math.pi,math.pi)#随机向量方向 xlab=25+math.sin(rd2)*rd ylab=75+math.cos(rd2)*rd#随机点的坐标 x1[0][i]=xlab x1[1][i]=ylab#保存到x1中 ax.plot(xlab,ylab,color='red', marker='.')#图形化显示 for i in range(100):#随机生成第2类点 rd=random.uniform(0,25) rd2=random.uniform(-math.pi,math.pi) xlab=75+math.sin(rd2)*rd ylab=25+math.cos(rd2)*rd x2[0][i]=xlab x2[1][i]=ylab ax.plot(xlab,ylab,color='blue', marker='.') M1=np.zeros(2) M2=np.zeros(2) for i in range(100): for j in range(2): M1[j]=M1[j]+0.01*x1[j][i]#求第一类点的重心 for i in range(100): for j in range(2): M2[j]=M2[j]+0.01*x2[j][i]#求第二类点的重心 ax.plot(M1[0],M1[1],color='black',marker='+',markersize=12)#将重心输出 ax.plot(M2[0],M2[1],color='black',marker='+',markersize=12) Sw=np.zeros((2,2))#求总类内离散度矩阵Sw for i in range(100): Sw=Sw+0.01*np.mat(x1[:,i]-M1).T*np.mat(x1[:,i]-M1) +0.01*np.mat(x2[:,i]-M2).T*np.mat(x2[:,i]-M1) w=np.dot(np.linalg.pinv(Sw),(M1-M2))#求出方向向量 w=np.mat(w.T) midPoint=(M1+M2)/2#阈值 x=range(0,100) y=[] for i in range(100): y.append(-float(w[0][0])/float(w[1][0])*(i-float(midPoint[0]))+float(midPoint[1])) #print(y) ax.plot(x,y,color='green',marker='*') plt.show()
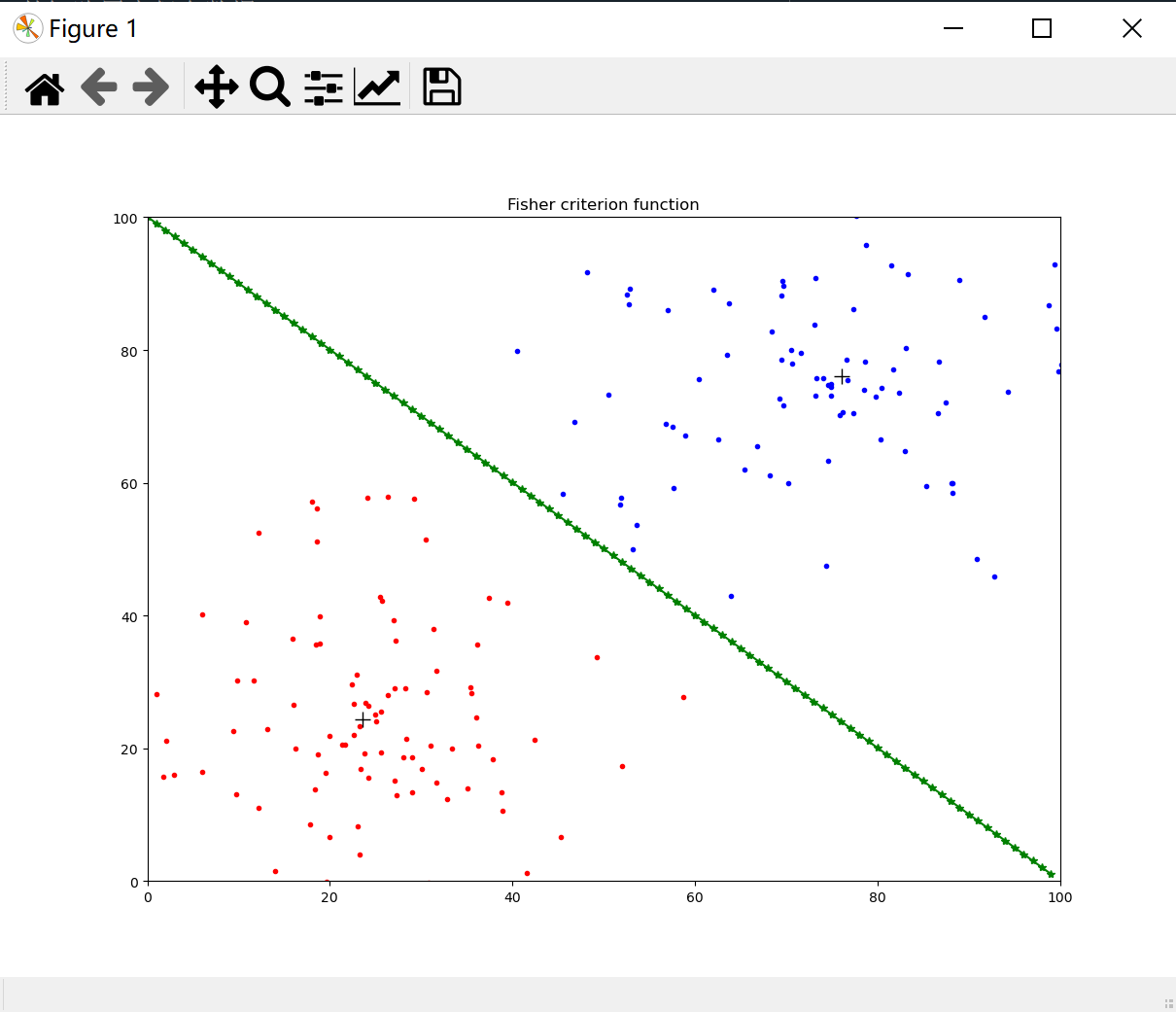
附:向量求导
附:拉格朗日乘数法
基本形态:求函数$z=f(x,y)$在满足$\varphi(x,y)=0$条件下的极值,可以转化为函数$F(x,y,\lambda)=f(x,y)+\lambda\varphi(x,y)$的无条件极值问题,其中λ为参数。
令$F(x,y,\lambda)$对$x$和$y$和$\lambda$的一阶偏导数等于零,即
$$F'_x=ƒ'_x(x,y)+\lambda\varphi'_x(x,y)=0$$
$$F'_y=ƒ'_y(x,y)+\lambda\varphi'_y(x,y)=0$$
$$F'_{\lambda}=\varphi(x,y)=0$$
由上述方程组解出$x$,$y$及$\lambda$,如此求得的$(x,y)$,就是函数$z=ƒ(x,y)$在条件$\varphi(x,y)=0$下的可能极值点。