01二维卷积

二维卷积

在图像处理中，图像是以二维矩阵的形式输入到神经网络中的，因此，需要二维卷积。

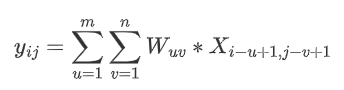
计算过程

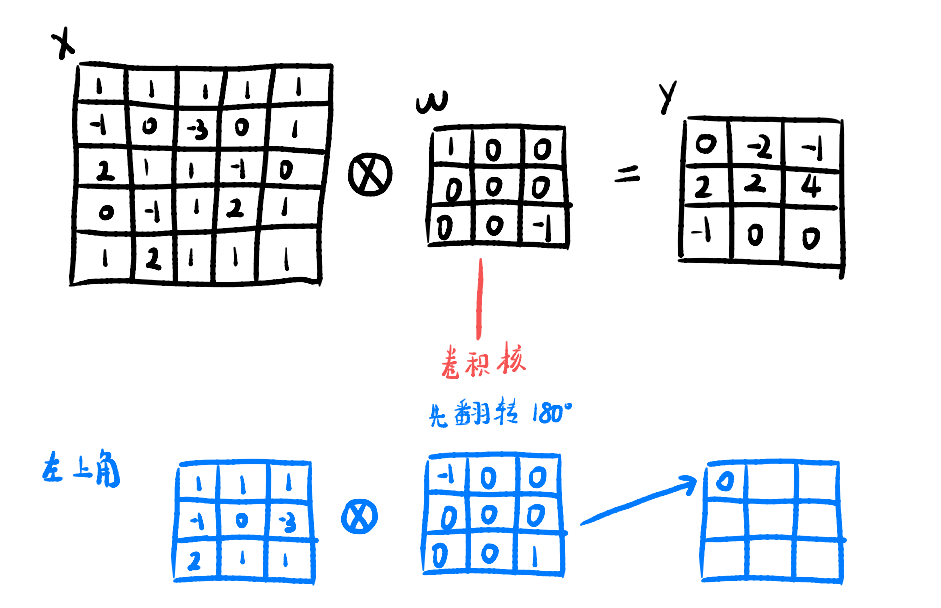
互相关

计算卷积时需要卷积核翻转

卷积核操作的目标是特征提取

翻转是不必要的！！！

互相关：

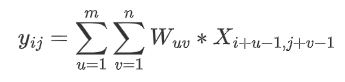
除非特别申明，卷积一般指互相关

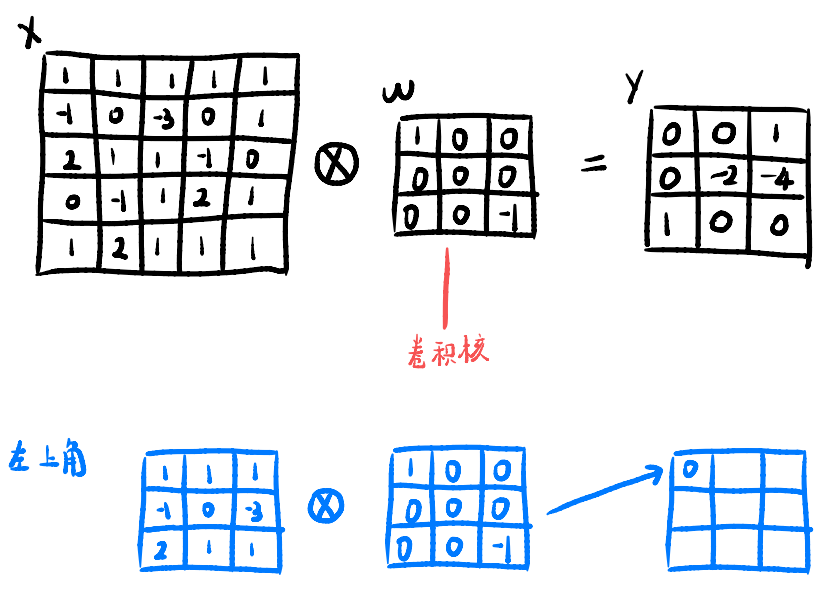
二维卷积代码实现

实现效果：可以通过输入矩阵和卷积核，实现任意大小的二维卷积

实现过程：

• 卷积核翻转
• 取出每一个框
• 做内积

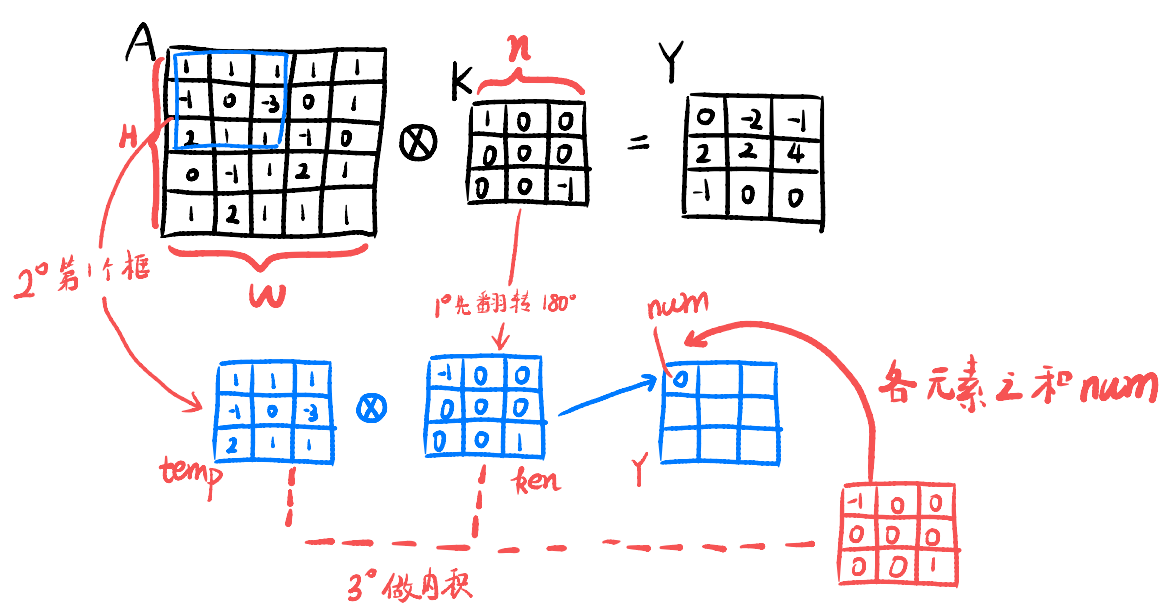
step1：卷积核翻转

定义FZ()函数，使卷积核矩阵旋转180°

若互相关不需要翻转，可注释

def fz(a):
    return a[::-1]
def FZ(mat):
    return np.array(fz(list(map(fz, mat))))

step2：取出每一个框

• 框的大小 = 卷积核大小

  kuang = np.zeros[n, n]

• 框的个数 = 循环个数

  w = W - n + 1

  h = H - n + 1

step3：做内积

• 框 x 卷积核 = temp矩阵

  temp = np.multiply(kuang, ken)

• temp矩阵中各元素之和 = num

  num = temp.sum()

• num放入最后的矩阵Y中

  Y[u, v] = num

完整代码

# 奶酥手写二维卷积
import numpy as np

# 用函数FZ()实现卷积核的翻转
def fz(a):
    return a[::-1]
def FZ(mat):
    return np.array(fz(list(map(fz, mat))))

#  用函数Juan()实现卷积
def Juan(img, H, W, kernel, n):
    # img：输入矩阵；H是行,W是列；kernel：卷积核；n：卷积核大小
    # 最后return的是矩阵大小是(H-n+1) x (W-n+1)
    w = W - n + 1
    h = H - n + 1
    ken = kernel
    # 矩阵翻转是卷积，不用翻转是互相关，可注释
    ken = FZ(kernel)

    # 定义最后的结果Y矩阵，大小是 h x w
    # kuang的大小和卷积核大小一样，是 n x n
    Y = np.zeros([h, w])
    kuang = np.zeros([n, n])
    for v in range(w):
        for u in range(h):
            for i in range(n):
                for j in range(n):
                    kuang[i, j] = img[i + u, j + v]
            temp = np.multiply(kuang, ken)
            num = temp.sum()
            # 这里可以输出卷积过后的每一各num
            # print(sum)
            # 将每一个num放入到Y矩阵中，
            Y[u, v] = num
    return Y


if __name__ == '__main__':
    A = np.array([[1, 1, 1, 1, 1],
                  [-1, 0, -3, 0, 1],
                  [2, 1, 1, -1, 0],
                  [0, -1, 1, 2, 1],
                  [1, 2, 1, 1, 1]])  # 5行5列
    K = np.array([[1, 0, 0], [0, 0, 0], [0, 0, -1]])
    # A输入矩阵；5,5矩阵的行和列；K卷积核，3卷积核的大小。
    print(Juan(A, 5, 5, ken, 3))

输出结果

[[ 0. -2. -1.]
 [ 2.  2.  4.]
 [-1.  0.  0.]]

可以用任意矩阵来尝试。

    '''
    A = np.array([[1, 1, 1, 1, 1], 
                  [1, 1, 1, 1, 1], 
                  [1, 1, 1, 1, 1], 
                  [1, 1, 1, 1, 1]])  # 4行5列
                  
    K = np.array([[2, 2, 2], 
                  [2, 2, 2], 
                  [2, 2, 2]])
    print(Juan(A, 4, 5, K, 3))
    '''

    '''
    A = np.array([[1, 2, 3, 4, 5],
                  [6, 7, 8, 9, 10],
                  [11, 12, 13, 14, 15]])  # 3行5列
                  
    K = np.array([[1, 1, 1], 
                  [1, 1, 1], 
                  [1, 1, 1]])
    print(Juan(A, 3, 5, ken, 3))     
    '''

    '''
    A = np.array([[1, 1, 1, 1, 1],
                    [-1, 0, -3, 0, 1],
                    [2, 1, 1, -1, 0],
                    [0, -1, 1, 2, 1],
                    [1, 2, 1, 1, 1]])  # 5行5列
                    
    ken = np.array([[1, 0, 0], 
                    [0, 0, 0], 
                    [0, 0, -1]])
    print(Juan(A, 5, 5, ken, 3))
    '''

卷积作为特征提取器

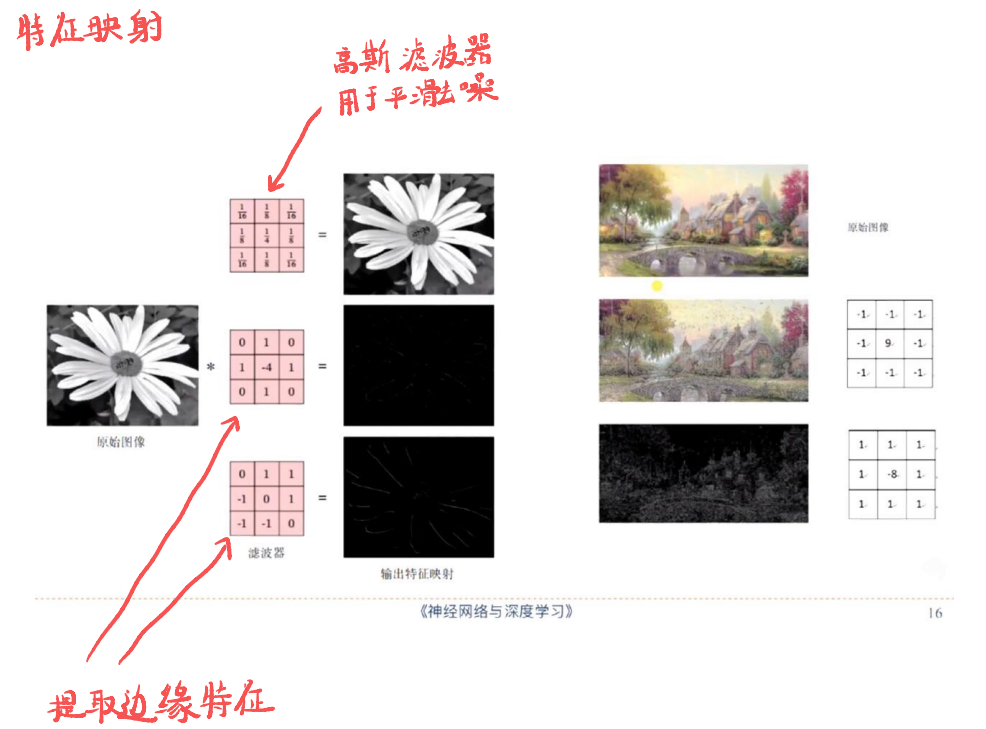
代码不想放