19神经网络实现手写识别

神经网络实现手写识别

任务介绍

手写数字识别是一个多分类问题，共有10个分类，每个手写数字图像的类别标签是0~9中的其中一个数。例如下面这三张图片的标签分别是0，1，2。

任务：利用sklearn来训练一个简单的全连接神经网络，即多层感知机（Multilayer perceptron，MLP）用于识别数据集DBRHD的手写数字。

MLP的输入

DBRHD数据集的每个图片是一个由0或1组成的32 X 32的文本矩阵。
多层感知机的输入为图片矩阵展开的1 X 1024个神经元。

由于数据集的标签数字只能作为类别判别而不具有数值大小作用，即类别之间并无优先高低之分。

MLP的输出

MLP输出：“one-hot vectors“

一个one-hot向量除了某一位的数字是1以外其余各维度数字都是0。
图片标签将表示成一个只有在第n维度（从0开始）数字为1的10维向量。比如，标签0将表示成[1,0,0,0,0,0,0,0,0,0]。即,MLP输出层具有10个神经元。

MLP结构

MLP的输入与输出层，中间隐藏层的层数和神经元的个数设置都将影响该MLP模型的准确率。
在本实例中，我们只设置一层隐藏层，在后续实验中比较该隐藏层神经元个数为50、100、200时的MLP效果。

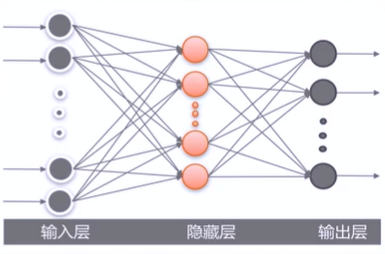
MLP手写识别实例构建

实现步骤：

步骤1:建立工程并导人sklearn包
步骤2:加载训练数据
步骤3:训练神经网络
步骤4:测试集评价

具体步骤

步骤1：建立工程并导入sklean包

（1)创建MLP.py文件

（2）在MLP.py文件中导入sklearn相关包

步骤2：加载训练数据

（1）定义img2vector函数，将加载的32*32的图片矩阵展开成一列向量。

（2）定义加载训练数据的函数readDataSet，并将样本标签转化为one-hot向量。

（3）调用readDataSet和img2vector函数加载数据，将训练的图片存放在train_dataSet中，对应的标签则存在train_hwLabels中。

步骤3：训练神经网络

（1）构建神经网络：设置网络的隐藏层数、各隐藏层神经元个数、激活函数、学习率、优化方法、最大迭代次数。

设置含100个神经元的隐藏层。
hidden layer sizes存放的是一个元组，表示第i层隐藏层里神经元的个数。
使用logistic激活函数和adam优化方法，并令初始学习率为0.0001，迭代2000次。

（2）构建神经网络：设置网络的隐藏层数、各隐藏层神经元个数、激活函数、学习率、优化方法、最大迭代次数。

（3）使用训练数据训练构建好的神经网络。

fit函数能够根据训练集及对应标签集自动设置多层感知机的输入与输出层的神经元个数。
例:train_dataSet为n X 1024的矩阵，train hwLabels为n X 10的矩阵,则fit函数将MLP的输入层神经元个数设为1024，输出层神经元个数为10。

步骤4：测试集评价

（1)加载测试集。

（2）使用训练好的MLP对测试集进行预测，并计算错误率。

具体代码

import numpy as np  # 导入numpy工具包
from os import listdir  # 使用listdir模块，用于访问本地文件
from sklearn.neural_network import MLPClassifier


def img2vector(fileName):
    """ 将加载的32*32的图片矩阵展开成一列向量"""
    retMat = np.zeros([1024], int)  # 定义返回的矩阵，大小为1*1024
    fr = open(fileName)  # 打开包含32*32大小的数字文件
    lines = fr.readlines()  # 读取文件的所有行
    for i in range(32):  # 遍历文件所有行
        for j in range(32):  # 并将01数字存放在retMat中
            retMat[i * 32 + j] = lines[i][j]
    return retMat


def readDataSet(path):
    """加载训练数据，并将样本标签转化为one-hot向量"""
    fileList = listdir(path)  # 获取文件夹下的所有文件
    numFiles = len(fileList)  # 统计需要读取的文件的数目
    dataSet = np.zeros([numFiles, 1024], int)  # 用于存放所有的数字文件
    hwLabels = np.zeros([numFiles, 10])  # 用于存放对应的one-hot标签
    for i in range(numFiles):  # 遍历所有的文件
        filePath = fileList[i]  # 获取文件名称/路径
        digit = int(filePath.split('_')[0])  # 通过文件名获取标签，注意类型转换
        hwLabels[i][digit] = 1.0  # 将对应的one-hot标签置1
        dataSet[i] = img2vector(path + '/' + filePath)  # 读取文件内容
    return dataSet, hwLabels


# 读取训练集
train_dataSet, train_hwLabels = readDataSet('digits/trainingDigits')

'''
构建神经网络：设置网络的隐藏层数、各隐藏层神经元个数、激活函数、学习率、优化方法、最大迭代次数。

设置含100个神经元的隐藏层,hidden_layer_sizes 存放的是一个元组，表示第i层隐藏层里神经元的个数
使用logistic激活函数和adam优化方法，并令初始学习率为0.0001，
后期改动数值，以及使用logistic激活函数和sgd优化方法
'''
clf = MLPClassifier(hidden_layer_sizes=(100,),
                    activation='logistic', solver='adam',
                    learning_rate_init=0.0001, max_iter=2000)
print(clf)
'''
fit函数能够根据训练集及对应标签集自动设置多层感知机的输入与输出层的神经元个数
例如train_dataSet为n*1024的矩阵，train_hwLabels为n*10的矩阵，则fit函数将MLP的输入层神经元个数设为1024，输出层神经元个数为10
'''

clf.fit(train_dataSet, train_hwLabels)

# 读取测试集
dataSet, hwLabels = readDataSet('digits/testDigits')
res = clf.predict(dataSet)  # 对测试集进行预测
error_num = 0  # 统计预测错误的数目
num = len(dataSet)  # 测试集的数目
for i in range(num):  # 遍历预测结果
    # 比较长度为10的数组，返回包含01的数组，0为不同，1为相同
    # 若预测结果与真实结果相同，则10个数字全为1，否则不全为1
    if np.sum(res[i] == hwLabels[i]) < 10:
        error_num += 1
print("Total num:", num, " Wrong num:", \
      error_num, "  TureRate:", 1-(error_num / float(num)))

实验效果

实验输出结果：

MLPClassifier(activation='logistic', learning_rate_init=0.0001, max_iter=2000)
Total num: 946  Wrong num: 42   TureRate: 0.9556025369978858

以下是改动各个参数，各隐藏层神经元个数，最大迭代次数，学习率的实验结果：

隐藏层神经元个数影响

运行隐藏层神经元个数为50、100、200的多层感知机，对比实验效果。

运行隐藏层神经元个数为50：

MLPClassifier(activation='logistic', hidden_layer_sizes=(50,),
              learning_rate_init=0.0001, max_iter=2000)
Total num: 946  Wrong num: 43   TureRate: 0.9545454545454546

运行隐藏层神经元个数为100：

MLPClassifier(activation='logistic', learning_rate_init=0.0001, max_iter=2000)
Total num: 946  Wrong num: 42   TureRate: 0.9556025369978858

运行隐藏层神经元个数为200：

MLPClassifier(activation='logistic', hidden_layer_sizes=(200,),
              learning_rate_init=0.0001, max_iter=2000)
Total num: 946  Wrong num: 37   TureRate: 0.9608879492600423

随着隐藏层神经元个数的增加,MLP的正确率持上升趋势。
大量的隐藏层神经元带来的计算负担与对结果的提升并不对等，因此，如何选取合适的隐藏神经元个数是一个值得探讨的问题。

迭代次数影响分析：

设隐藏层神经元个数为100，初始学习率为0.0001，最大迭代次数分别为500、1000、1500、2000。

最大迭代次数分别为500：

MLPClassifier(activation='logistic', learning_rate_init=0.0001, max_iter=500)
Total num: 946  Wrong num: 54   TureRate: 0.9429175475687104

最大迭代次数分别为1000：

MLPClassifier(activation='logistic', learning_rate_init=0.0001, max_iter=1000)
Total num: 946  Wrong num: 40   TureRate: 0.9577167019027484

最大迭代次数分别为1500：

MLPClassifier(activation='logistic', learning_rate_init=0.0001, max_iter=1500)
Total num: 946  Wrong num: 41   TureRate: 0.9566596194503171

最大迭代次数分别为2000：

MLPClassifier(activation='logistic', learning_rate_init=0.0001, max_iter=2000)
Total num: 946  Wrong num: 33   TureRate: 0.9651162790697675

过小的迭代次数可能使得MLP早停，造成较低的正确率。
当最大迭代次数>1000时，正确率基本保持不变，这说明MLP在第1000迭代时已收敛，剩余的迭代次数不再进行。
—般设置较大的最大迭代次数来保证多层感知机能够收敛，达到较高的正确率。

学习率影响分析：

改用随机梯度下降优化算法即将MLPclassifer的参数( solver='sgd',），设隐藏层神经元个数为100，最大迭代次数为2000，学习率分别为:0.1、0.01、0.001、0.0001。

学习率为0.1：

MLPClassifier(activation='logistic', learning_rate_init=0.1, max_iter=2000,solver='sgd')
Total num: 946  Wrong num: 33   TureRate: 0.9651162790697675

学习率为0.01：

MLPClassifier(activation='logistic', learning_rate_init=0.01, max_iter=2000,solver='sgd')
Total num: 946  Wrong num: 39   TureRate: 0.9587737843551797

学习率为0.001：

MLPClassifier(activation='logistic', max_iter=2000, solver='sgd')
Total num: 946  Wrong num: 47   TureRate: 0.9503171247357294

学习率为0.0001：

MLPClassifier(activation='logistic', learning_rate_init=0.0001, max_iter=2000,solver='sgd')
Total num: 946  Wrong num: 242   TureRate: 0.7441860465116279

结论：较小的学习率带来了更低的正确率，这是因为较小学习率无法在2000次迭代内完成收敛，而步长较大的学习率使得MLP在2000次迭代内快速收敛到最优解。因此，较小的学习率一般要配备较大的迭代次数以保证其收敛。

最后的思考

这次的代码比较简单，就是需要花时间理解。

这次的程序需要导入数据集digits.rar放在文件目录下。

在看懂了代码之后，自己修改运行了一下，发现得到的数据和视频教学里得到的数据还是有差距的，绝知此事要躬行啊。

这两天在转团关系，累累的。

posted @ 2021-10-26 22:03 奶酥阅读(709) 评论(0) 编辑收藏举报

刷新页面返回顶部

奶酥