17岭回归
岭回归及其应用实例
线性回归
对于一般地线性回归问题,参数的求解采用的是最小二乘法,其目标函数如下:
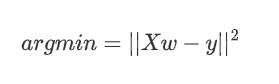
参数w的求解,也可以使用以下矩阵方法进行:
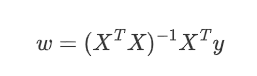
对于矩阵X,若某些列线性相关性较大(即训练样本中某些属性线性相关),就会导致XTX的值接近0,在计算(XTX)-1时就会出现不稳定性。
结论:传统的基于最小二乘的线性回归法缺乏稳定性。
岭回归
岭回归的出现就是为了解决最小二乘的线性回归法缺乏稳定性。
岭回归的优化目标:
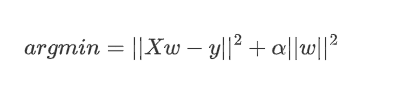
对应矩阵求解方法为:
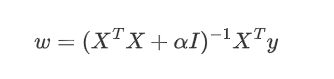
- 岭回归(ridge regression)是一种专用于共线性数据分析的有偏估计回归方法。
- 是一种改良的最小二乘估计法,对某些数据的拟合要强于最小二乘法。
sklearn中的岭回归
在sklearn库中,可以使用sklearn.linear_model.Ridge调用岭回归模型,主要参数:
- alpha,正则化因子,对应于损失函数中的α。
- fit_intercept:表示是否计算截距。
- solver:设置计算参数的方法,可选参数’auto'、‘svd'、'sag'等。
交通流量预测实例
数据介绍:数据为某路口的交通流量监测数据,记录全年小时级别的车流量。
实验目的:根据已有的数据创建多项式特征,使用岭回归模型代替一般的线性模型,对车流量的信息进行多项式回归。
技术路线:sklearn.linear_model.Ridgefrom
sklearn.preprocessing.PolynomialFeatures
数据实例:
- HR:一天中的第几个小时(0-23 )
- WEEK_DAY:一周中的第几天(0-6)
- DAY_OF_YEAR:一年中的第几天(1-365)
- WEEK_OF_YEAR:一年中的第几周(1-53)
- TRAFFIC COUNT:交通流量
全部数据集包含2万条以上数据(21626)
程序编写
1、建立工程,导人sklearn相关工具包
2、数据加载
3、数据处理
4、划分训练集和测试集
5、创建回归器,并进行训练
6、画出拟合曲线
具体代码
import numpy as np
import pandas as pd
from sklearn.linear_model import Ridge # 加载岭回归方法
# from sklearn import cross_validation 这个会报错
# 由于 pyfm 2016.2.10版本的源码中还使用cross_validate进行交叉验证,而**cross_validate这个包早就不在使用了,已经划分到了model_selection包中。
from sklearn.model_selection import cross_validate
from sklearn import model_selection
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures # 用于创建多项式特征,如ab、 a2、 b2
data = pd.read_csv('traffic flow.csv')
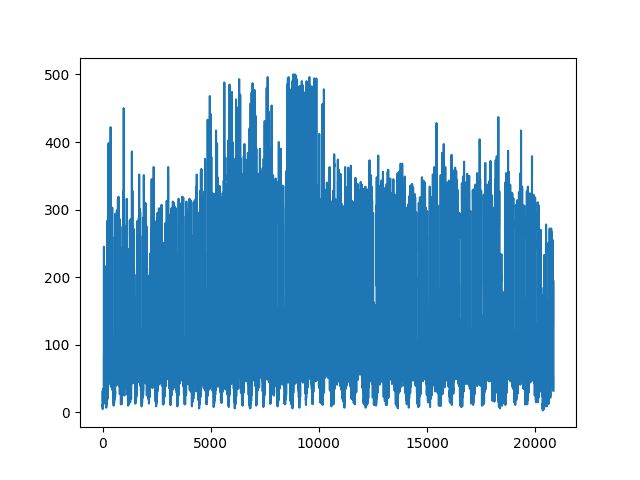
# 绘制车流量信息
plt.plot(data['TRAFFIC_COUNT'])
plt.show()
X = data[data.columns[1:5]] # 属性数据
y = data['TRAFFIC_COUNT'] # 车流量数据(即是要预测的数据)
poly = PolynomialFeatures(5) # 测试后5是效果较好的一个参数
# X为创建的多项式特征
X = poly.fit_transform(X)
# 将所有数据划分为训练集和测试集,test_size表示测试集的比例,random_state是随机数种子
train_set_X, test_set_X, train_set_y, test_set_y = model_selection.train_test_split(X, y, test_size=0.3,
random_state=0)
# 创建岭回归实例
clf = Ridge(alpha=1.0, fit_intercept=True)
# 调用fit函数使用训练集训练回归器
clf.fit(train_set_X, train_set_y)
# 利用测试集计算回归曲线的拟合优度,clf.score返回值为0.7375
# 拟合优度,用于评价拟合好坏,最大为1,无最小值,当对所有输入都输出同一个值时,拟合优度为0。
clf.score(test_set_X, test_set_y)
start = 200 # 接下来我们画一段200到300范围内的拟合曲线
end = 300
y_pre = clf.predict(X) # 是调用predict函数的拟合值
time = np.arange(start, end)
plt.plot(time, y[start:end], 'b', label="real")
plt.plot(time, y_pre[start:end], 'r', label='predict')
# 展示真实数据(蓝色)以及拟合的曲线(红色)
plt.legend(loc='upper left') # 设置图例的位置
plt.show()
结果分析
车流量信息
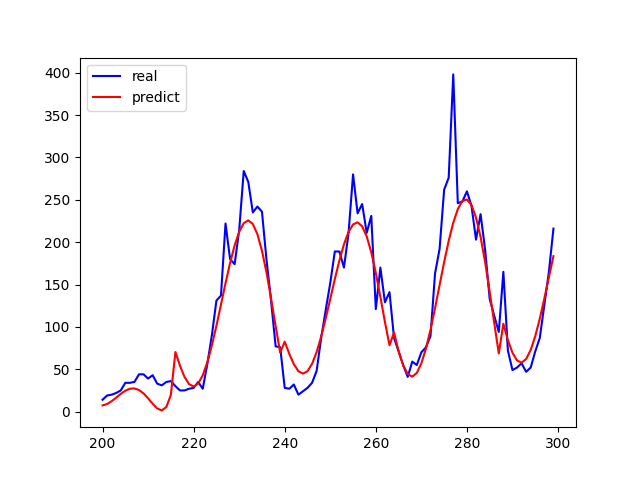
拟合曲线
取200到300范围,内的拟合曲线
展示真实数据(蓝色)以及拟合的曲线(红色)
分析结论:预测值和实际值的走势是大致相同的
最后的思考
1、from sklearn import cross_validation导入出错
from sklearn import cross_validation
# 报错NameError: name 'model_selection' is not defined
由于 pyfm 2016.2.10 版本的源码中还使用cross_validate进行交叉验证,而cross_validate这个包早就不在使用了,已经划分到了model_selection包中。
解决方法:将开头的导入修改为from sklearn import model_selection
查找源码中的 cross_validate ,替换为 model_selection
搞到晚上终于写完了,代码有一点点小问题,之前遇到过类似的所以丝毫不慌。
今天我的手发炎了,害,不知道什么时候能好。



