【scoi2009】围豆豆(最短路模型)
洛谷题面:https://www.luogu.org/problemnew/show/P2566
由每个豆子引一条射线,与射线交点个数为奇数相当于多边形围住了它,这样可以定义一个状态f[x][y][s]表示从起点出发,走到(x,y)处时的路径与D颗豆子引出的射线相交的奇偶性状态为s,最少需多少步。然后跑最短路转移即可。
然而,有一个小问题就是转移时如何判与豆子引出的射线相交。如果单纯按与线相交的拐点来计算的话,我们发现会有这两种截然不同的情况被算成了一样。
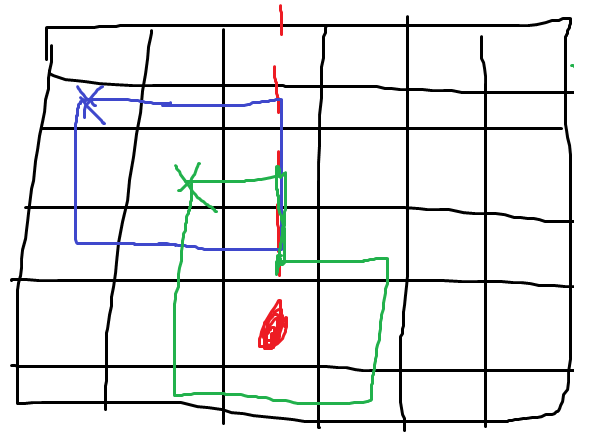
理论上蓝色路径应该是0,绿色路径应该是1才对。
于是我们可以选择统计时把边定一下向,像绿色路径这种穿出的情况就不重复计算了。详见代码。
#include<bits/stdc++.h>
using namespace std;
const int N = 15;
#define min(a,b) ((a)<(b)?(a):(b))
#define rep(i,a,b) for(register int i=(a);i<=(b);++i)
int n,m,w[N],val[1<<10],D;
char mp[N][N];
int dis[N][N][1<<10],ans;
struct la{int x,y,s;}bean[N];
queue<la> q;
bool vis[N][N][1<<10];
int rx[4]={0,1,0,-1};
int ry[4]={1,0,-1,0};
inline bool isin(int x,int y){return x>=1&&x<=n&&y>=1&&y<=m;}
inline void spfa(int x,int y){
memset(dis,0x3f,sizeof(dis));
q.push((la){x,y,0});dis[x][y][0]=0;vis[x][y][0]=1;
while(!q.empty()){
la u=q.front();q.pop();vis[u.x][u.y][u.s]=0;
rep(i,0,3){
int nx=u.x+rx[i],ny=u.y+ry[i],ns=u.s;
if(!isin(nx,ny)||mp[nx][ny]!='0')continue;
rep(j,0,D-1){
if(ny>bean[j].y&&((nx==bean[j].x&&u.x>bean[j].x)||(nx>bean[j].x&&u.x==bean[j].x)))ns^=(1<<j);
}
if(dis[nx][ny][ns]>dis[u.x][u.y][u.s]+1){
dis[nx][ny][ns]=dis[u.x][u.y][u.s]+1;
if(vis[nx][ny][ns])continue;
vis[nx][ny][ns]=1;
q.push((la){nx,ny,ns});
}
}
}
}
int main(){
scanf("%d%d",&n,&m);
scanf("%d",&D);
rep(i,0,D-1){
scanf("%d",&w[i]);
}
rep(j,0,(1<<D)-1){
rep(i,0,D-1){
if(j&(1<<i))val[j]+=w[i];
}
}
rep(i,1,n){
scanf("%s",mp[i]+1);
rep(j,1,m){
if(mp[i][j]>'0')bean[mp[i][j]-'0'-1]=(la){i,j,0};
}
}
rep(i,1,n){
rep(j,1,m){
if(mp[i][j]!='0')continue;
spfa(i,j);
rep(k,0,(1<<D)-1)ans=max(ans,val[k]-dis[i][j][k]);
}
}
printf("%d\n",ans);
return 0;
}
When everthing changes,nothing changes.



