代码改变世界

线性回归与梯度下降法[二]——优化与比较

2016-12-25 21:09  Fururur  阅读(3245)  评论(0)  编辑  收藏  举报

接着上文——机器学习基础——梯度下降法（Gradient Descent）往下讲。这次我们主要用matlab来实现更一般化的梯度下降法。由上文中的几个变量到多个变量。改变算法的思路，使用矩阵来进行计算。同时对算法的优化和调参进行总结。即特征缩放（feature scaling）问题和学习速率\(\alpha\)的取值问题。还有在拟合线性模型时，如何选择正确的算法，梯度下降 or 最小二乘法？

matlab的基本用法，已经总结在matlab基础教程——根据Andrew Ng的machine learning整理上。相对于python来说，的确matlab的语法更简单，上手更快，只要简单学习下就能上手编写算法，或者用于计算。

matlab实现一般梯度下降法

针对于Andrew Ng的machine learning课当中的数据，我们这里给出了matlab的一般梯度下降法的代码。
在了解了算法原理后，实现起来就非常简单了，主要分为以下几步:

  1. 数据加载和预处理
    从文件中读入数据，并分块放到相应的矩阵中去。这里我们选取的模型是\(y = \theta_0+\theta_1x_1\)。显然\(x_0\)取1，所以需要在原有的X矩阵中添加一列全1的列。
data = load ('data1.txt');
X = data(:, 1);
y = data(:, 2);
X = [ones(length(data),1),data(:,1)];
  1. 设置算法的学习参数
X = [ones(length(data),1),data(:,1)];
theta = zeros(2,1);%theta初始值为0
alpha = 0.01;
max_iter = 5000;
m = length(y);%数据组数
J_history = zeros(max_iter,1);%初始化迭代误差变量
  1. 执行算法。
for iter = 1:max_iter
	theta = theta - alpha / m * X' * (X * theta - y);	%梯度下降
    J_history(iter) = sum((X * theta-y) .^ 2) / (2*m);	%记录每次 迭代后的全局误差
    fprintf('iter:%d ------ Error:%f\n',iter,J_history(iter));
end

下面是完整的代码：https://github.com/maoqyhz/machine_learning_practice

%加载数据和数据预处理
data = load ('data1.txt');
fprintf('Running Gradient Descent ...\n');

X = data(:, 1); 	%取X集合
y = data(:, 2);		%取y集合

%画出数据的散点图
figure;
plot(X, y, 'rx', 'MarkerSize', 10);
ylabel('Profit in $10,000s'); 
xlabel('Population of City in 10,000s'); 
hold on; 

%设置学习参数
X = [ones(length(data),1),data(:,1)]; 	% y = theta0*x0 + theta1*x1 默认x0为1
theta = zeros(2,1);	%theta初始值为0
alpha = 0.01;
max_iter = 5000;

m = length(y);	%数据组数
J_history = zeros(max_iter,1);	%初始化迭代误差变量
iter = 1;
for iter = 1:max_iter
	%每迭代100次画一条曲线
    if  mod(iter,100) == 0
        plot(X(:,2), X*theta, 'g')
    end

	theta = theta - alpha / m * X' * (X * theta - y);	%梯度下降
    J_history(iter) = sum((X * theta-y) .^ 2) / (2*m);	%记录每次迭代后的全局误差
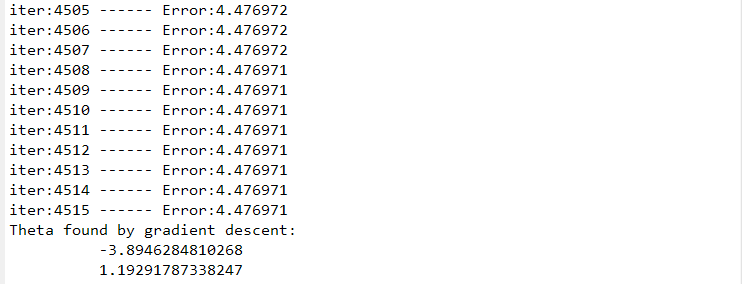
    fprintf('iter:%d ------ Error:%f\n',iter,J_history(iter));
end

%输出最终的theta值和最终的拟合曲线
disp('Theta found by gradient descent:');
disp(theta);
plot(X(:,2), X*theta, 'k')
legend('Training data', 'Linear regression')
hold off

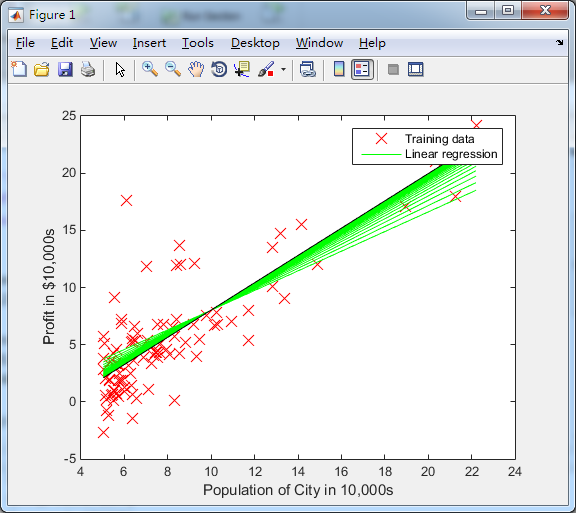
运行结果如下：

  • 图1为得到的结果，可以看到在现有的学习速率下，基本上4600次左右就能收敛了。得出了最终的\(\theta\)值。

  • 图2为拟合的过程，每迭代100次会画出一条绿色曲线，不断迭代最终收敛的曲线是黑色的那条，可以清楚看见拟合的过程。

特征缩放和数据的归一化

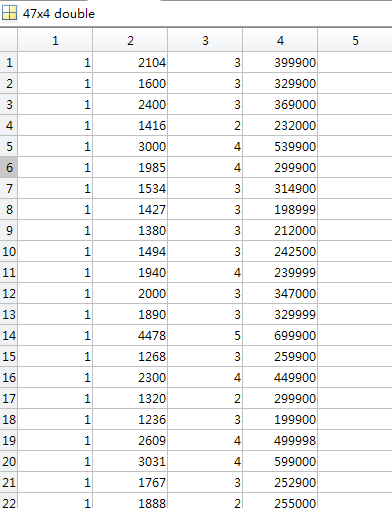
下图为上例中的数据部分，可以看到第一列和第二列的数据差距并不大，所以不需要很多的迭代次数就能收敛。但是如果数据之间差距很大，在计算过程中会导致数据超出数据类型的最大存储值，或者是需要额外的迭代次数来到达收敛的情况，所以此时我们对数据进行处理，也就是所说的特征缩放。

数据归一化

数据归一化是非常有用的特征缩放方法，可以把数据缩放到\([-1,1]\)中。常见的归一化方法有两种。

min-max标准化（Min-Max Normalization）

可以使数据进行线性变换，使结果值映射到\([0,1]\)之间。设原区间为\([a,b]\)，转换函数如下：

\[x^* = \frac{x-a}{b-a} \]

Z-score标准化方法（Z-socre Normalization）

这种方法给予原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化。经过处理的数据符合标准正态分布，即均值为0，标准差为1，转化函数为：

\[x^* = \frac{x-\mu}{\sigma} \]

其中\(\mu\)为数据的均值，\(\sigma\)为数据的标准差。

matlab来处理数据归一化问题

新的数据集如下，显然，不同的特征之前的差距比较大，此时就需要进行归一化处理。

  1. 数据归一化
%Z-score Normalization
function [ X_norm,avg,sigma ] = normalize(X)
	avg = mean(X,1); %均值
	sigma = std(X,1);%标准差
	%repmat函数用来数据填充
	X_norm  = (X - repmat(avg,size(X,1),1)) ./  repmat(sigma,size(X,1),1);
end
  1. 测试样本需要进行归一化。
% 使用1 1650 3对数据进行估计
x = [1650 3];
price = [1 (([1650 3] - avg) ./ sigma)] * theta ;

学习速率的取值

可以看到学习速率太小，需要进行多次迭代才能收敛；学习速率太大，可能会miss最小值儿无法收敛。因此我们需要选取合适的学习速率Andrew Ng已经告诉我们方法，如图所示，选择学习速率的区间，不断地去调整以满足自己的数据和算法。说到底机器学习就是个调参的过程，啊哈哈~~

梯度下降法VS最小二乘法

对于线性回归问题，我们既可以用梯度下降法也可以用最小二乘法来解决。那么这两种算法有和不同？简而言之，前者是需要多次迭代来收敛到全局最小值，后者则是提供一种解析解法，直接一次性求得\(\theta\)的最优值。

对于最小二乘法，我们这里只给出具体的结论。证明牵涉到矩阵的求导，可以直接看西瓜书。

那么，当\(X^TX\)为满秩矩阵或正定矩阵时，我们可以一步得到\(\theta\)的最优值。

\[\theta = (X^TX)^{-1}X^Ty \]

而在matlab中，最小二乘法的求解过程也的确只需要一行代码就可以完成。把下面的代码替换掉梯度下降的代码即可。

theta = pinv( X' * X ) * X' * y;

How to choose？

梯度下降法

  • 需要设置学习速率。
  • 需要进行多次迭代。
  • 数据比较大时（百万？），可以很好的工作。

最小二乘法

  • 不需要设置学习速率。
  • 不需要迭代。
  • 需要矩阵计算，数据大时，计算速度慢。

参考文献