[笔记]均分纸牌问题
Index
- 链形均分纸牌
- 每次仅可交换\(1\)张
- 每次可交换多张
- 环形均分纸牌
- 每次仅可交换\(1\)张
- 每次可交换多张
拓展性很强的贪心问题。或许能推广到树之类的结构上,或者拓展到方案计数问题之类,不过目前还没想好啦。
链形均分纸牌
每次仅可交换\(1\)张
最基础的例题是这样的:
有\(n\)个人坐成一排,第\(i\)个人初始持有\(a[i]\)张纸牌。定义一次操作如下:
- 设\((u,v)\)是相邻的两人,让\(u\)给\(v\)一张纸牌。
请问要让每个人持有的纸牌数相同,最少进行多少次操作。
此题可以用贪心求解。
显然,有解\(\iff n|(\sum\limits_{i=1}^{n}a[i])\),令\(a\)的平均数为\(x\)。
令\(s\)为\(a\)的前缀和数组,答案即为\(\sum\limits_{i=1}^{n}|s[i]-i\times x|\)。
也可以将每个\(a[i]\)减去\(x\)再用,答案就是\(\sum\limits_{i=1}^{n}|s[i]|\)了。
这是因为第\(1\)个人的牌数只能通过第\(2\)个人调整成\(x\),显然两个相邻的人之间只能进行单向操作,否则答案一定不优。所以第\(1\)个人被调整成\(x\)后就相当于被删掉了,相应地,第\(2\)个人只能通过第\(3\)个人调整成\(x\)……答案就这样出来了。
固然,按上面的模拟方法,可能会出现负数张牌的情况。不过每个人最终都会被补成\(x\)张牌,所以通过更改交换顺序就可以保证中途不出现负数张牌(实际上感性理解并不难,下面是严谨一点的证明)。
更为具体地,我们不妨令\(a[i]\leftarrow (a[i]-x)\),令\(y\)表示此时的\(\min a[i]\)。
我们需要证明,最优方案下一定可以保证任何时刻\(a[i]\ge y\)。
对于\(a[1,i]\)和\(a[i+1,n]\)两个区间:
- 如果\(s[i]=0\),那么两个区间不进行交换。
- 如果\(s[i]>0\),那么一定左给右。
- 如果\(s[i]<0\),那么一定右给左。
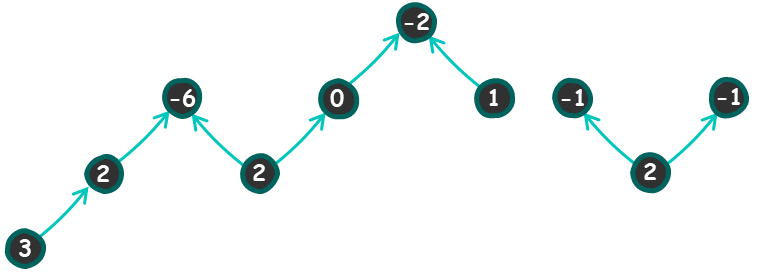
我们把这样的交换关系用箭头表示出来。
每个元素只能发牌给自己指向的元素,且只能收到指向自己元素的牌。
我们按上图的拓扑序发牌,按拓扑序遍历到的当前元素,一定将所有可能拿到的牌都拿到了,自然其值一定\(\ge y\)。对于每种图的形态,这样的构造都是可行的。
点击查看代码
#include<bits/stdc++.h>
#define N 100010
using namespace std;
int n,a[N];
int solve(){
int x=0,ans=0;
for(int i=1;i<=n;i++) x+=a[i];
if(x%n) return -1;
x/=n;
for(int i=1;i<=n;i++) a[i]+=a[i-1]-x;
for(int i=1;i<=n;i++) ans+=abs(a[i]);
return ans;
}
signed main(){
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
cout<<solve()<<"\n";
return 0;
}
每次可交换多张
将上题的条件修改了一下。
和上面的图一样的分析方式,令\(a[i]\leftarrow (a[i]-x)\),答案即为箭头个数,也即和非\(0\)的前缀个数。
点击查看代码
#include<bits/stdc++.h>
#define N 100010
using namespace std;
int n,a[N];
int solve(){
int x=0,ans=0;
for(int i=1;i<=n;i++) x+=a[i];
if(x%n) return -1;
x/=n;
for(int i=1;i<=n;i++) a[i]+=a[i-1]-x;
for(int i=1;i<=n;i++) ans+=(a[i]!=0);
return ans;
}
signed main(){
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
cout<<solve()<<"\n";
return 0;
}
环形均分纸牌
每次仅可交换\(1\)张
所谓环形,就是规定第\(1\)个人和第\(n\)个人也可以互相发牌。
结论:一定存在一个解,满足它是最优的,且至少有两个相邻的人之间没有纸牌传递。
证明:
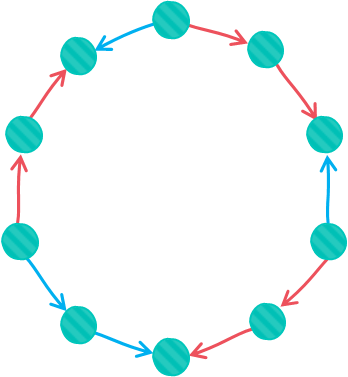
假设所有相邻两人之间都发生传递(自然,都是单向的),如下图。
用每个箭头传递的纸牌数\(k\)作为它的权值,如果它是红箭头则看作\(+k\),是蓝箭头则看作\(-k\)。那么容易知道,相邻的两个箭头的和是定值。
换句话说,只要确定一个箭头传递的纸牌数,其他箭头传递的纸牌数也就确定了。
我们从上图中选定一个红色箭头,让它的值\(+1\),考虑对答案的贡献。此时所有红色箭头的值都会\(+1\),所有蓝色箭头的值都会\(-1\),对答案的贡献设为\(+y\);如果让这个红色箭头的值\(-1\),对答案的贡献就是\(-y\)。
我们根据\(y\)的正负性选择\(+\)或\(-\),直到某个箭头变成\(0\),这样就存在相邻两人之间没有传递了,答案要么不变,要么减少。
有了这个结论之后,我们就可以枚举环在哪里断开,对于每条链计算答案,不过这样是\(O(n^2)\)的,考虑优化。
链从\(k\)和它之后的元素处断开,新链的前缀和\(s_k\)为:
答案即为\(\sum\limits_{i=1}^n |s_k[i]-i\times x|\)。
设\(s'[i]\)为\(s[i]-i\times x\),则有\(s[i]=s'[i]+i\times x\),且\(s'[n]=0\),带入可得:
答案即为\(\sum\limits_{i=1}^n |s_k[i]-i\times x|=\sum\limits_{i=1}^n|s'[i]-s'[k]|\)。
呼 这个转化似乎很难想的说……不过仔细想来,\(s'\)就是将\(a[i]\leftarrow (a[i]-x)\)后的\(s\)啊!如果想到这个步骤就好考虑了(其实上面这堆都是我用它倒退得来的)。
上面这个式子是一个典型的“货仓选址”问题,\(s'[k]\)选在\(s'[1\sim n]\)的中位数时答案最小。而取中位数可以用nth_element()做到\(O(n)\)。
总时间复杂度是\(O(n)\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define N 1000010
using namespace std;
int n,a[N],s[N];
int solve(){
int x=0,ans=0;
for(int i=1;i<=n;i++) x+=a[i];
if(x%n) return -1;
x/=n;
for(int i=1;i<=n;i++) s[i]=s[i-1]+a[i]-x;
nth_element(s+1,s+(n+1)/2,s+1+n);
for(int i=1;i<=n;i++) ans+=abs(s[i]-s[(n+1)/2]);
return ans;
}
signed main(){
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
cout<<solve()<<"\n";
return 0;
}
附另一种推导过程,部分来自此题解 by Social_Zhao。
设\(K[i]\)为\(i\)给他前一个人的牌数。
则有\(a[i-1]-K[i-1]+K[i]=x\),即\(K[i]=K[i-1]+x-a[i-1]\)。
这样我们就可以用\(K[1]\)表示出\(K[2\sim n]\),这里的结论和证明中提到的“只要确定一个箭头传递的纸牌数,其他箭头传递的纸牌数也就确定了”是相同的,更具体地:
答案即为\(\sum\limits_{i=1}^n |K[i]|=\sum\limits_{i=1}^n|K[1]+ix-s[i]|\),然后货仓选址即可,代码相同不放了。
两种推导过程有异曲同工之妙。
每次可交换多张
这种情况下,显然只有破环成链才可能取到最优解。
枚举断开位置仍然效率太低,考虑优化。
结合链\(2\)和环\(1\)的结论,可知答案是\(\sum\limits_{i=1}^n [s'[i]-s'[k]\neq 0]\)。为了让答案尽可能小,\(s'[k]\)应取\(s'\)的众数。
点击查看代码
#include<bits/stdc++.h>
#define N 1000010
using namespace std;
int n,a[N];
unordered_map<int,int> cnt;
int solve(){
int x=0,ans=0;
for(int i=1;i<=n;i++) x+=a[i];
if(x%n) return -1;
x/=n;
for(int i=1;i<=n;i++){
a[i]+=a[i-1]-x;
cnt[a[i]]++;
}
for(auto i:cnt) ans=max(ans,i.second);
return n-ans;
}
signed main(){
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
cout<<solve()<<"\n";
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号