[笔记]多重背包的优化(二进制,单调队列)
朴素多重背包
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
for(int k=1;k*w[i]<=m&&k<=cnt[i];k++){
f[i][j]=f[i-1][j];
if(j>=w[i]) f[i][j]=max(f[i][j],f[i-1][j-k*w[i]]+k*v[i]);
}
}
}
空间优化后:
for(int i=1;i<=n;i++){
for(int j=m;j>=w[i];j--){
for(int k=1;k*w[i]<=m&&k<=cnt[i];k++){
f[j]=max(f[j],f[j-k*w[i]]+k*v[i]);
}
}
}
时间复杂度是\(O(m\sum\limits_{i=1}^n cnt[i])\),有两种优化方式:
二进制拆分优化
主要思想在于重新计算物品,转化成0-1背包。
将\(cnt[i]\)拆分成\(2^0+2^1+2^2+\dots +2^x+y\)的形式,比如\(34=1+2+4+8+16+3\),拆分成的每个数\(x\)看作一个体积为\(w\times x\)、价值为\(v\times x\)的新物品。对于第\(i\)种物品,只要选择数量\(\in [1,cnt[i]]\),就可以用这些新物品的组合来表示。
所以拆完之后直接按照0-1背包来跑就可以了。物品\(i\)拆成新物品的个数是\(\log cnt[i]\)数量级的。所以时间复杂度是\(O(m\sum\limits_{i=1}^n \log cnt[i])\)。
拆完再跑
#include<bits/stdc++.h>
#define N 102
#define M 40010
#define int long long
using namespace std;
int n,m,w[N*20],v[N*20],f[M],idx;
signed main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
int wi,vi,cnt,k=1;
cin>>vi>>wi>>cnt;
cnt=min(cnt,m/wi);
while(cnt>=k) w[++idx]=wi*k,v[idx]=vi*k,cnt-=k,k<<=1;
if(cnt>0) w[++idx]=wi*cnt,v[idx]=vi*cnt;
}
for(int i=1;i<=idx;i++)
for(int j=m;j>=w[i];j--)
f[j]=max(f[j],f[j-w[i]]+v[i]);
cout<<f[m];
return 0;
}
边拆边跑
#include<bits/stdc++.h>
#define int long long
#define N 102
#define W 40002
using namespace std;
int n,m,f[W];
signed main(){
cin>>n>>m;
while(n--){
int w,v,cnt;
cin>>v>>w>>cnt;
cnt=min(cnt,m/w);
for(int i=1;i<=cnt;i<<=1){
for(int j=m;j>=i*w;j--)
f[j]=max(f[j],f[j-i*w]+i*v);
cnt-=i;
}
if(!cnt) continue;
for(int j=m;j>=cnt*w;j--)
f[j]=max(f[j],f[j-cnt*w]+cnt*v);
}
cout<<f[m]<<"\n";
return 0;
}
单调队列优化
观察板子代码,我们发现\(f[j]\)由\(f[j-kw]\)转移而来,所以我们可以按取模\(w\)的的值相同将\(f\)分成若干组,每个组单独考虑(如下图,红色部分是一组,单项箭头表示状态转移)。
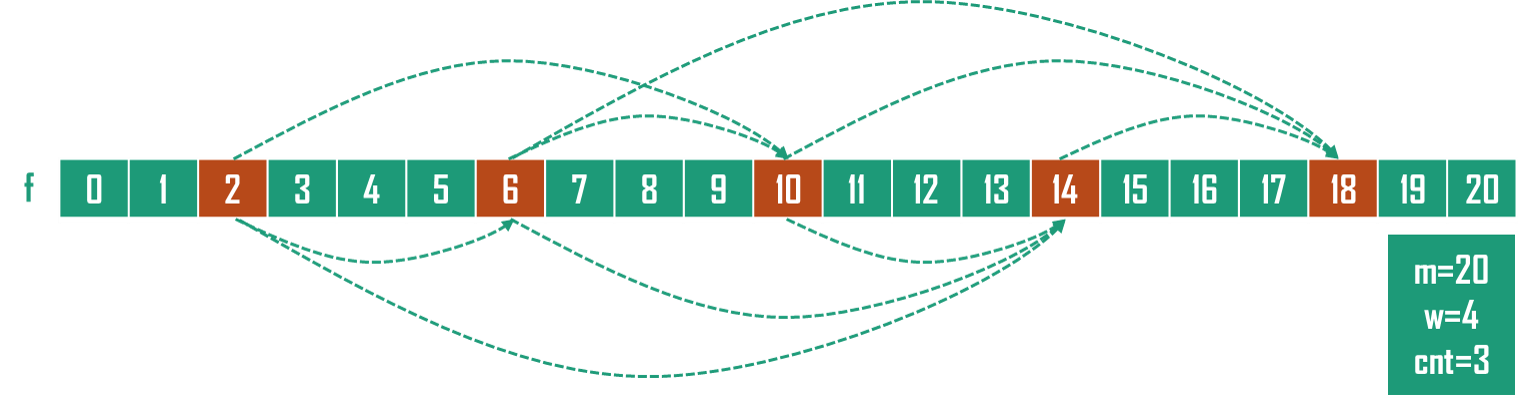
背包大小\(m\)取模\(w\)的值为\(d\)的组,包括的状态有:\(d,d+w,d+2w,\dots,d+kw\),其中我们重新定义\(k=\lfloor\frac{m-d}{w}\rfloor\)。
有转移:\(f[d+jw]=\max\{f[d+j'w]+(j-j')\times v\}\),其中\(j'\)满足\(j'\in [\max(0,j-cnt),j)\)。
上面的式子改写一下,\(f[d+jw]=\max\{f[d+j'-j'v\}+jv\)。\(\max\)里的东西用单调队列维护即可。
时间复杂度\(O(nm)\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define N 102
#define M 40010
using namespace std;
int n,m,head,tail,q[M],q2[M],f[M];//q存下标,q2存值
signed main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
int w,v,cnt;
cin>>v>>w>>cnt;
cnt=min(cnt,m/w);
for(int d=0;d<w;d++){
head=1,tail=0;
int k=(m-d)/w;//同余于d的状态共有k+1个:d,d+w,d+2w,...,d+kw
for(int j=0;j<=k;j++){
while(head<=tail&&f[d+j*w]-j*v>=q2[tail]) tail--;
q[++tail]=j,q2[tail]=f[d+j*w]-j*v;
while(q[head]<j-cnt) head++;
f[d+j*w]=max(f[d+j*w],q2[head]+j*v);
}
}
}
cout<<f[m]<<"\n";
return 0;
}
\(\color{#b2b2b2}\text{Phantasmagoria of Flower View.}\)

