[笔记]KMP算法 - 下（例题）
CF1200E Compress Words ~ 洛谷
给定\(n\)个字符串，请按下面的规则，从左往右依次合并\(n\)个字符串，成为\(1\)个字符串：
- 将\(A,B\)合并，就是找到最大的\(i\)，使得\(A\)的长为\(i\)的后缀和\(B\)的长为\(i\)的前缀相等，删除\(A\)的这个后缀，并将\(B\)连接到它的后面。
注意每次应该将第\(i\)个字符串与\(1\sim (i-1)\)合并后的结果进行新的一轮合并，而非输入字符串之间合并。
\(n\le 10^5\)，字符串总长\(\le 10^6\)。
我们考虑\(A,B\)合并，其实就是找到\(A\)的后缀 和 \(B\)的前缀的最长共同部分，然后删掉其中一个，再把\(A,B\)连接起来。比如ABCDCD和CDCDEF的共同部分就是那个CDCD。
怎么找这个共同部分呢？
我们设T=B+'~'+A，那么\(T\)的最长公共前后缀就是我们要求的最长公共部分，而这个最长公共前后缀可以直接套用KMP的\(nxt\)数组。
为什么要隔一个~呢？因为不隔的话，我们找的公共部分会重叠，导致错误。
还需要注意的是，如果每次都把当前的答案\(S\)和新字符串\(A\)连接在一起，时间复杂度就是\(O(n^2)\)。而我们知道公共部分的长度就是\(\min(\)S.size()\(,\)A.size()\()\)，所以应该先截取一下，让T.size()\(<2*\)A.size()。这样时间复杂度就是\(O(n)\)了。
点击查看代码
#include<bits/stdc++.h>
#define N 1000010
using namespace std;
int t,n,m,nxt[N];
string s,a;
int main(){
cin>>t;
while(t--){
cin>>a;
n=s.size(),m=a.size();//为了拼接更方便，下标从0开始
int minlen=min(n,m);
string ts=a.substr(0,minlen)+'~'+s.substr(n-minlen,minlen);
int tn=ts.size();
for(int i=1,j=0;i<tn;i++){
while(ts[i]!=ts[j]&&j) j=nxt[j-1];
nxt[i]=(ts[i]==ts[j]?++j:0);//别忘了置0
}//nxt[tn-1]就是重合部分的长度
s+=a.substr(nxt[tn-1],m);//小技巧，超出边界自动调整
}
cout<<s<<"\n";
return 0;
}
其中代码第\(18\)行用到一个小技巧，string.substr(pos,size)，意为从\(pos\)开始截取\(size\)个字符，如果\(pos+size-1\)超过右边界，会自动调整到右边界，不要误以为代码中的\(m\)就是右边界哦。
还有，参数\(size\)是允许超界的，但如果参数\(pos>\)string.size()会RE！
另外，这道题也可以用字符串哈希做，不过KMP比哈希快一倍（可能是因为字符串哈希要双哈希，所以有\(2\)倍常数）。
P4824 [USACO15FEB] Censoring S
给定字符串\(A,B\)，请重复下面的操作，直到\(A\)中不存在\(B\)：
- 删除\(A\)中最靠前的\(B\)。
请输出最后的\(A\)。
（注意删除\(B\)之后，两端的字符串可能拼接成一个新的\(B\)）
\(1\le |B|\le |A|\le 10^6\)
我们可以想到，建立一个栈，依次加入\(i\)指针。如果中途凑成一个\(B\)则把这些元素删掉。而判断凑成\(B\)就可以用KMP。
在KMP的过程中进行比对，如果凑出一个\(B\)，就把匹配的下标全部出栈，所谓删掉，其实就是把\(j\)指针回溯成之前的状态，即变成出栈后栈顶\(i\)指针所对应的\(j\)。所以我们用\(t[i]\)来表示\(i\)指针所对应的\(j\)指针，出栈后\(j\)设为\(t[st[top]]\)即可。
点击查看代码
#include<bits/stdc++.h>
#define N 1000010
using namespace std;
string a,b;
int n,m,nxt[N],t[N],st[N],top;
int main(){
cin>>a>>b;
n=a.size(),m=b.size();
for(int i=1,j=0;i<m;i++){
while(b[i]!=b[j]&&j) j=nxt[j-1];
nxt[i]=(b[i]==b[j]?++j:0);
}
for(int i=0,j=0;i<n;i++){
while(a[i]!=b[j]&&j) j=nxt[j-1];
t[i]=j,st[++top]=i;
if(a[i]==b[j]){
if(j==m-1) top-=m,j=t[st[top]];
j++;
}
}
for(int i=1;i<=top;i++) cout<<a[st[i]];
return 0;
}
P3435 [POI2006] OKR-Periods of Words
给定字符串\(S\)，请求出\(S\)每个前缀的答案之和。
定义字符串\(T\)的答案为：
- 如果存在字符串\(P\)是\(T\)的真前缀，且\(T\)是\(P+P\)的前缀，则答案就是\(P\)可能的最长长度。
- 如果不存在字符串\(P\)，则答案为\(0\)。
题面看上去有点绕，但其实找一找规律：
如上图，红色部分是整个字符串的答案。
可以发现黑色部分其实就是这个字符串的“最短非空公共前后缀”。
所以先跑一遍KMP的前半部分，把\(nxt\)数组求出来。
然后遍历每个前缀，不断沿着\(nxt\)数组往前跳，直到找到该前缀的“最短非空公共前后缀”长度，记为\(j\)。
对于长度为\(i\)的前缀，如果\(j=0\)，则答案不累加；否则答案累加\(i-j\)即可。
但是这样做会超时，不妨利用记忆化的思想，\(j\)每跳一下，就把\(nxt[i]\)更新为最新的\(j\)，这样其他\(j\)再跳到\(i\)这个位置就能直接得到答案了。
点击查看代码
#include<bits/stdc++.h>
#define N 1000010
using namespace std;
int n,nxt[N];
long long ans;
string s;
int main(){
cin>>n>>s;
s=' '+s;//下标从1开始
for(int i=2,j=1;i<=n;i++){
while(s[i]!=s[j]&&j>1) j=nxt[j-1]+1;
if(s[i]==s[j]) nxt[i]=j++;
}
for(int i=1;i<=n;i++){
int j=nxt[i];
while(nxt[j]) j=nxt[i]=nxt[j];
if(j) ans+=i-j;
}
cout<<ans<<"\n";
return 0;
}
P2375 [NOI2014] 动物园
多测，每次给定字符串\(S\)，请求出：
\(\prod\limits_{i=1}^{n} num[i]+1\ (\text{mod}\ 10^9+7)\)
其中\(num[i]\)表示\(S\)长度为\(i\)的前缀的“公共不重叠前后缀”的个数。
例如\(S=\)ADABCADA，则\(num[3]=1,num[5]=0,num[8]=2\)。
首先这道题是要我们求个数，我们先不管这个“不重叠”的条件，用\(num[i]\)表示\(S\)长度为\(i\)的前缀的“公共前后缀”（包含自身，原因待会会说）个数，递推即可求得，具体来说，\(num[i]=num[nxt[i]]+1,\ num[0]=0,\ num[1]=1\)。
考虑前后缀不能重叠，其实就是在重叠的基础上往前跳，不断求更小的公共前后缀，直到大小\(\le \lfloor \frac{i}{2}\rfloor\)。所以我们加一个循环，和求\(nxt\)方法相似，我们同样添加一个指针\(j\)，和\(nxt[i]\)含义类似，不过要时刻限制\(j\)不能超过\(i\)的一半。对于每个\(i\)计算出的\(j\)，累乘\(num[j]+1\)即可。
我们发现这里\(j\)本身就是“长度不超过\(\frac{i}{2}\)的最长公共前后缀的长度”，因此\(num\)计算时，自己也是要算的，这就是为什么\(num[i]\)囊括的公共前后缀要包括自己。
点击查看代码
#include<bits/stdc++.h>
#define mod 1000000007
#define N 1000010
using namespace std;
int t,n,nxt[N],num[N];
long long ans=1;
string s;
int main(){
cin>>t;
num[1]=1;
while(t--){
cin>>s;
ans=1;
n=s.size(),s=' '+s;
for(int i=2,j=1;i<=n;i++){
while(s[i]!=s[j]&&j>1) j=nxt[j-1]+1;
nxt[i]=(s[i]==s[j]?j++:0);
num[i]=num[j-1]+1;
}
for(int i=2,j=1;i<=n;i++){//i从1开始会死循环
while(s[i]!=s[j]&&j>1) j=nxt[j-1]+1;
while(j>(i>>1)) j=nxt[j-1]+1;
if(s[i]==s[j]) j++;
ans=ans*(num[j-1]+1)%mod;
}
cout<<ans<<"\n";
}
return 0;
}
UVA1328 Period
多测，每次给定一个字符串\(S\)，请你找出\(S\)的所有是周期串的前缀：
周期串的定义：
- \(R\)是一个周期串，当且仅当\(R\)可以通过若干个字符串\(T\)连接而成（\(T\neq R\)）。
对于每个周期串前缀，请输出该前缀的长度，以及该前缀最多能包含多少个\(T\)。
首先我们有一个结论：对于\(S\)的长度为\(i\)的前缀，只要\(nxt[i]\neq 0\)且\((i-nxt[i])\mid i\)，就说明它是周期串，而且最小周期为\(i-nxt[i]\)。
有这个结论，直接模拟就可以了，因为要求的是最多数量，所以用总长度\(\div\)最小周期得出。
我们现在证明“\(S\)是周期串\(\iff (n-nxt[n])|n\)”。
充分性 - \((n-nxt[n])|n \Longrightarrow S\)是周期串
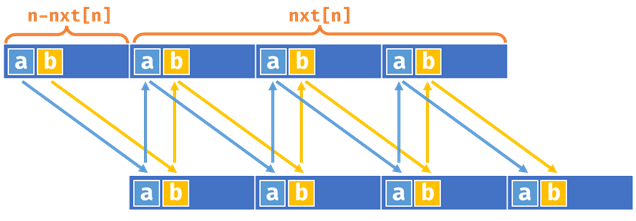
如上图，我们把\(S\)复制一份，对其公共前后缀。那么我们可以按图中箭头来推演，因为\((n-nxt[n])|n\)，所以可以推演到最后，即说明\(S\)是周期串。
必要性 - \(S\)是周期串\(\Longrightarrow (n-nxt[n])|n\)
如果\(S\)是周期串，那么显然存在最小周期，而最小周期一定是\((n-nxt[n])\)（可以反证，如果存在更小的周期，那么\(nxt[n]\)也存在更大值，不成立），所以\((n-nxt[n])|n\)。
点击查看代码
#include<bits/stdc++.h>
#define N 1000010
using namespace std;
int n,nxt[N],testid;
string s;
int main(){
while(cin>>n){
if(!n) break;
cin>>s;
cout<<"Test case #"<<++testid<<"\n";
s=' '+s;
for(int i=2,j=1;i<=n;i++){
while(s[i]!=s[j]&&j>1) j=nxt[j-1]+1;
nxt[i]=(s[i]==s[j]?j++:0);
if(nxt[i]&&i%(i-nxt[i])==0) cout<<i<<" "<<i/(i-nxt[i])<<"\n";
}
cout<<"\n";
}
return 0;
}
双倍经验（稍有不同）：UVA10298 Power Strings
P4391 [BOI2009] Radio Transmission 无线传输
给定一个长度为\(n\)的字符串\(S\)，已知它是由若干个字符串\(R\)拼接而成的字符串\(R'\)的子串。
求可能的\(|R|\)的最小值。
先给结论：答案就是\(n-nxt[n]\)。
证明：和上一题很像，只不过\(S\)可以不是周期串，只需要是周期串的子串即可，所以不用限制\((n-nxt[n])|n\)，结论显然是相同的。
点击查看代码
#include<bits/stdc++.h>
#define N 1000010
using namespace std;
int n,nxt[N];
string s;
int main(){
cin>>n>>s;
s=' '+s;
for(int i=2,j=1;i<=n;i++){
while(j>1&&s[i]!=s[j]) j=nxt[j-1]+1;
nxt[i]=(s[i]==s[j]?j++:0);
}
cout<<n-nxt[n];
return 0;
}
嗯，就这样。
字符串中的\(nxt\)数组也可以叫做border，关于它又有一套border理论，其中也有涉及到后面\(2\)题的周期（period）；有关KMP的还有个失配树。不过这些我也没有专门去了解，等以后再说吧~~
