[笔记]KMP算法 - 上（算法详解）

算法详解

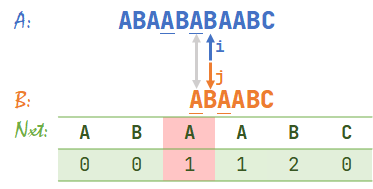
KMP 是一种字符串匹配算法，可以在线性的时间复杂度内解决字符串的“模式定位”问题，即：
在字符串 \(A\) 中查找字符串 \(B\) 出现的所有位置。

我们称 \(A\) 为主串，\(B\) 为模式串。下文都用 \(n\) 表示 \(A\) 的长度，\(m\) 表示 \(B\) 的长度，下标从 \(1\) 开始。

初始状态，我们用两个指针 \(i,j\) 分别指向 \(A\) 和 \(B\) 的第 \(1\) 位。

KMP 的主过程如下（后面会证明它的正确性）：

• 如果 \(A[i]=B[j]\)，则i++，j++。
• 如果 \(A[i]\neq B[j]\)：
  • 如果 \(j>1\)，则j=nxt[j-1]+1。
  • 如果 \(j\le 1\)，则i++。

其中，\(nxt\) 数组是一个用于表示发生失配后，\(j\) 回退到的位置。具体求法待会会说，下面我们用一个例子来理解 \(nxt\) 的功能，我将 \(nxt\) 数组画在图片的下方了。

• 初始状态。\(i=1,j=1\)。
  
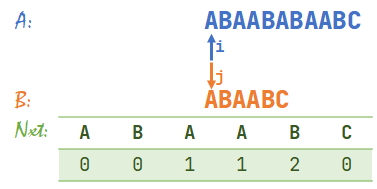
• \(A[i]=B[j]\)，同时右移 \(i,j\)。\(i=2,j=2\)。
  
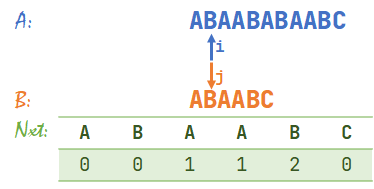
• \(A[i]=B[j]\)，同时右移 \(i,j\)。\(i=3,j=3\)。
  
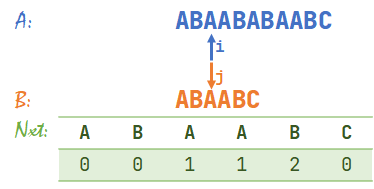
• \(A[i]=B[j]\)，同时右移 \(i,j\)。\(i=4,j=4\)。
  
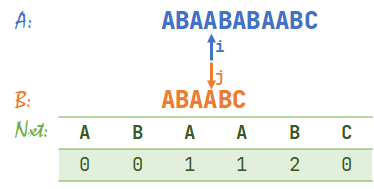
• \(A[i]=B[j]\)，同时右移 \(i,j\)。\(i=5,j=5\)。
  
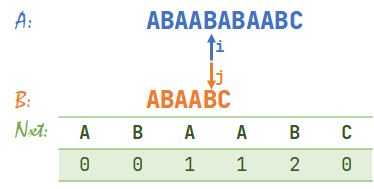
• \(A[i]=B[j]\)，同时右移 \(i,j\)。\(i=6,j=6\)。
  
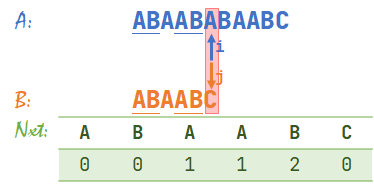
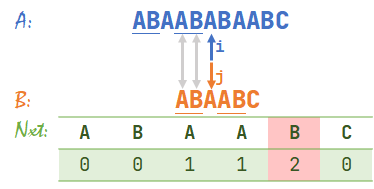
• 发现 \(A[i]\neq B[j]\)，于是查表 \(nxt[j-1]+1=nxt[5]+1=3\)，于是 \(j=3\)。此时 \(i=6\)。
  可以发现此时灰色箭头指向的两部分是相等的。
  进一步来说，从上一张图开始，下划线的部分都是相等的。
  
• OK我们继续，\(A[i]=B[j]\)，于是 \(i,j\) 同时右移，\(i=7,j=4\)。
  
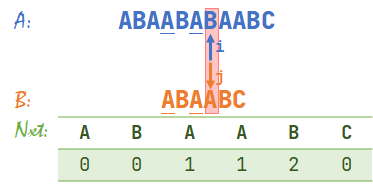
• 发现 \(A[i]\neq B[j]\)，查表得 \(nxt[3]+1=2\)，于是 \(j=2\)。此时 \(i=7\)。
  我们又发现 \(A\) 与 \(B\) 的下划线部分重合了，所以仍然可以从重合部分之后开始比较。
  
• 然后 \(A[i]=B[j]\)……就一直比到结束了，就不放图了w。

似乎2.2的情况没有提到呢……其实就是如果第 \(1\) 个字符就失配，就i++，这是很自然的。

我们可以把根据上面的过程（KMP 主过程）写出代码（下标从 \(1\) 开始）：

i=1,j=1;
while(i<=n){
	if(a[i]==b[j]) i++,j++;
	else if(j>1) j=nxt[j-1]+1;
	else i++;
	if(j==m+1) cout<<i-j+1<<"\n";
	//输出配对的开始位置，理解一下这里
}

可以发现 \(i\) 是始终不降的，比起暴力，KMP 通过避免 \(i\) 指针的回滚操作，减少了时间开销。

到这里我们已经可以初步理解 \(nxt\) 的含义，它是用来帮我们了解发生失配时，\(j\) 应该回退到什么位置。

再进一步分析，我们发现：\(nxt[x]\)，其实就是 \(B[1\sim x]\) 这一段的最长公共前后缀长度。

举个例子，YABAPQYABZABAAPYABAPQYABA。这是一个长度为 \(25\) 的字符串，那么当它作为 \(B\) 时：

• \(nxt[24]=9\)，如你所见，红色部分是 \(B[1\sim 24]\) 的公共前后缀，它的长度为 \(9\)。
• \(nxt[9]=3\)，因为YAB是 \(B[1\sim 9]\) 的公共前后缀，它的长度为 \(3\)。
• \(nxt[3]=0\)，因为 \(B[1\sim 3]\) 没有公共前后缀。
• \(nxt[25]=4\)，因为YABA是 \(B[1\sim 25]\) 的公共前后缀。

注意：公共前后缀可能有重叠部分，但是一个字符串不能作为它自己的公共前后缀（严格来说，我们把这种前/后缀称作真前/后缀，所以后面都带“真”来称呼了）。

公共真前后缀也可以称为border（不一定是最长），自然一个字符串可能有多个border。

我们规定，\(nxt[x]\) 表示的必须是 \(B[1\sim x]\) 这一段的最长公共真前后缀长度，这么定义是为了保证正确性，如果不规定最长，不能保证答案的正确性。后面的证明会提到。

现在我们的首要问题是，如何求 \(nxt\) 数组？

我们假定 \(i\) 之前的答案都已经求出，现在需要求 \(nxt[i]\)。

我们设 \(j\) 为 \(nxt[i-1]+1\)，如下图：

最简单的情况自然就是 \(B[i]=B[j]\)，那么 \(nxt[i]=j\)，这是显然的。

但是也可能遇到更棘手的情况：

\(B[i]\neq B[j]\)，怎么办呢？

既然YABAPQYAB这个公共真前后缀不行，那就再找一个更小的！

显然更小的前后缀就是YAB了，怎么得来的呢？就是看 \(nxt[j-1]\) 的值是多少，那么新的 \(j\) 就是 \(nxt[j-1]+1\)。此时再看看 \(B[i]=B[j]\) 是否成立。成立的话就 \(nxt[i]=j\)，不成立就继续找 \(j\)，直到找到 \(B[i]=B[j]\)，或者 \(j=1\) 为止。

可以发现我们充分利用了之前计算出的\(nxt\)，将原规模逐步缩小，是不是有点归纳法的意味？

再来举一个不断更新 \(j\) 直到 \(j=1\) 为止的例子：

我们可以把这一步骤也写成代码（下标从 \(1\) 开始）：

int i=2,j=1;//nxt[1]应为0，所以i从2开始
while(i<=m){
	if(b[i]==b[j]) nxt[i++]=j++;
	else if(j>1) j=nxt[j-1]+1;
	else nxt[i++]=0;
}

（是不是和上面的代码很像）

---

至此把两个代码拼接起来就能得到 KMP 的全过程了。

P3375 【模板】KMP

下标从 $1$ 开始

#include<bits/stdc++.h>
#define N 1000010
using namespace std;
string a,b;
int n,m,nxt[N];
int main(){
	cin>>a>>b;
	n=a.size(),m=b.size();
	a=' '+a,b=' '+b;
	int i=2,j=1;
	while(i<=m){
		if(b[i]==b[j]) nxt[i++]=j++;
		else if(j>1) j=nxt[j-1]+1;
		else nxt[i++]=0;
	}
	i=1,j=1;
	while(i<=n){
		if(a[i]==b[j]) i++,j++;
		else if(j>1) j=nxt[j-1]+1;
		else i++;
		if(j==m+1) cout<<i-j+1<<"\n";
	}
	for(int i=1;i<=m;i++) cout<<nxt[i]<<" ";
	return 0;
}

下标从 $0$ 开始

#include<bits/stdc++.h>
#define N 1000010
using namespace std;
string a,b;
int n,m,nxt[N];
int main(){
	cin>>a>>b;
	n=a.size(),m=b.size();
	int i=1,j=0;
	while(i<m){
		if(b[j]==b[i]) nxt[i++]=++j;
		else if(j) j=nxt[j-1];
		else nxt[i++]=0;
	}
	i=0,j=0;
	while(i<n){
		if(a[i]==b[j]) i++,j++;
		else if(j) j=nxt[j-1];
		else i++;
		if(j==m) cout<<i-j+1<<"\n";
	}
	for(int i=0;i<m;i++) cout<<nxt[i]<<" ";
	return 0;
}

正确性证明

我们刚接触 \(nxt\) 的定义时，可能会有疑问：为什么 \(nxt\) 一定要表示 \(B[1\sim x]\) 这一段的最长公共真前后缀长度？

我们证明一下 KMP 的正确性，顺带解决这个问题。

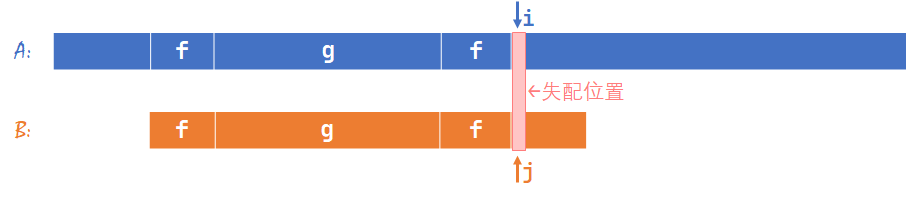
根据 KMP 的流程，如果遇到失配的情况，我们先找 \(B[1\sim (j-1)]\) 中的最长公共真前后缀（如图，用 \(f\) 表示）的长度 \(nxt[j-1]\)，然后把 \(j\) 置为 \(nxt[j-1]+1\)，如下图。

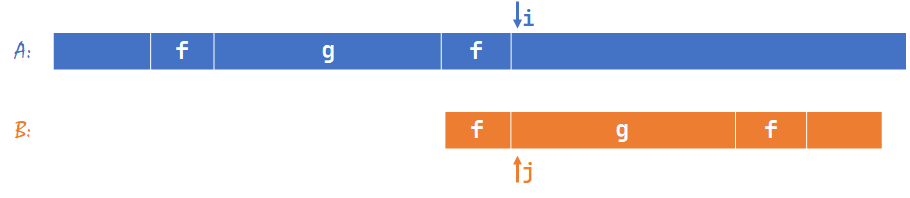
要证明 KMP 是正确的，首先需要证明 \(j\) 回退时不会跳过正确答案。
我们假设在 \(j>nxt[j-1]+1\) 时存在匹配，如下图，那么灰色箭头连接的部分都相等。
自然，黄色大括号部分（不包含 \(i,j\)）也相等，那么黄色部分的长度 \(=j-1\)。

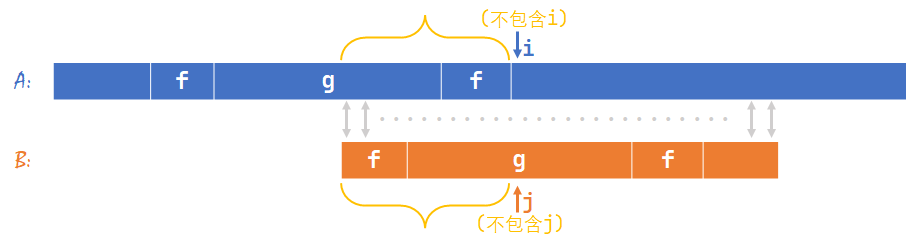
回到第 \(1\) 张图（\(j'\) 表示第 \(1\) 张图情况下的 \(j\)），根据假设，\(j>|f|+1\)，即黄色部分长度 \(>|f|\)。
这样的话，黄色部分就成了 \(B[1\sim j']\) 最长的公共真前后缀，与“\(f\) 是 \(B[1\sim j']\) 最长公共真前后缀”矛盾。

得到的结论是：\(j>nxt[j-1]+1\) 时一定不存在匹配。

这样我们的问题就迎刃而解了：如果 \(nxt\) 不是最长，上面的情况就可能不形成矛盾，进而 \(j>nxt[j-1]+1\) 时也可能存在解，而这被我们忽略掉了，所以正确性不能保证。

---

但正确性证明还没完，我们还需要考虑 \(j<nxt[j-1]+1\) 的情况。

事实上，这种情况是可能存在答案的，但我们可以证明，如果每次失配 \(j\) 都回退到 \(nxt[j-1]+1\)，一定可以把这种情况的答案找出来。

还是图 \(1\) 的初始状态，现在 \(A[i]\neq B[j]\)，发生失配。我们现在让 \(j<nxt[j-1]+1\)：

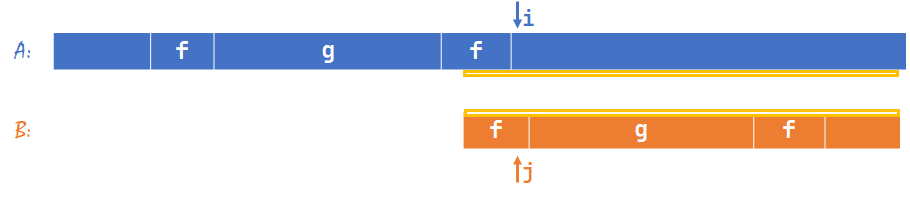
也就是 \(j\) 现在在 \(f\) 里面了。现在我们的问题是：如果这种情况下存在答案，我们按 \(j=nxt[j-1]+1\) 的步骤，是否能找出这个答案？
我们假设在 \(j<nxt[j-1]+1\) 中存在答案，如上图黄色线段所示。

现在我们让 \(j=nxt[j-1]+1\)：

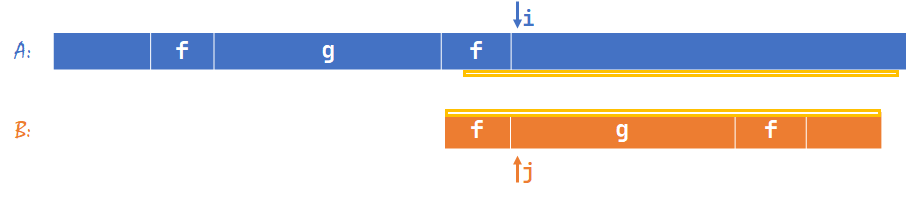
我们继续匹配，那么这一轮的失配位置一定 \(j\in [nxt[j−1]+1,m+1]\)（\(j=m+1\) 就是匹配成功）。
如下图，虚线位置即失配位置。

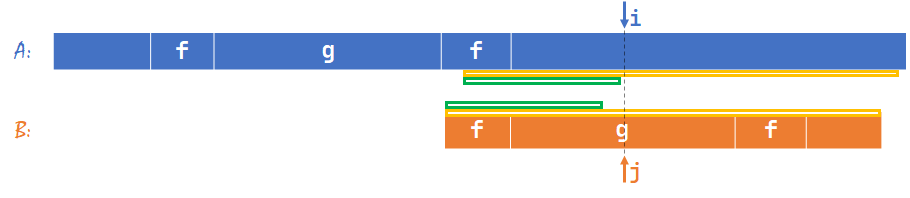
如上图，如果绿色线段就是 \(B[1\sim (j-1)]\) 的最长公共真前后缀，那么下一轮应该将两个绿色线段对齐继续匹配，这样黄色线段这个答案就被找到了。

如果不是呢？

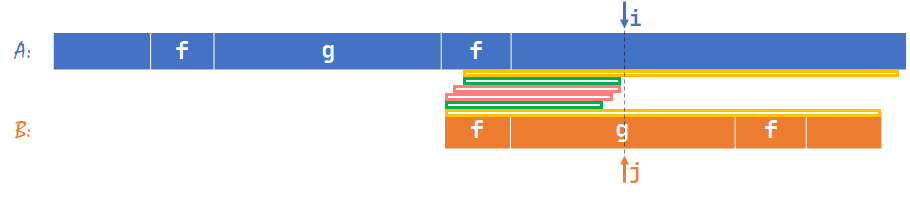
如上图，假设粉色部分是真正的公共前后缀，那么我们接下来应该把 \(j\) 回退到粉色的下一个位置：

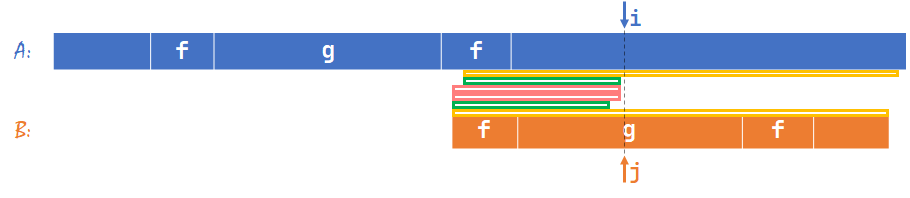
此时两个粉色重合。我们可以发现，这和上上张图的情形类似，只不过两个绿色离得更近了。这样重复上面的过程，再找第 \(1\) 个失配位置，不断逼近，总有一次绿色部分会成为 \(B[1\sim (j-1)]\) 的最长公共真前后缀。至此，我们证明了如果 \(j<nxt[j-1]+1\) 存在答案，按我们的方法一定能找到它。

综上，KMP 的正确性得证。

复杂度证明

通过看代码能发现两部分实现相似，所以就一块说了：

\(i\) 每增加 \(1\)，\(j\) 最多也增加 \(1\)，从而 \(j\) 最多增加 \(len\) 次，进而最多减少 \(len\) 次。
所以处理 \(nxt\) 是 \(O(m)\) 的，主过程是 \(O(n)\) 的，总时间复杂度就是 \(O(n+m)\) 了。

——字符串学习笔记 · 浅析KMP——单模式串匹配算法 - 皎月半洒花

细节

术语

我们前面提到的 \(nxt\) 数组，其实叫做PM表（Partial Match Table，部分匹配表）。

真正意义上的 \(next\) 数组，就是把PM表整体右移一位，最后一个值舍弃掉，然后在第 \(1\) 位补 \(-1\)。这个似乎并不常用，因为最后一个值舍弃掉了，所以只能匹配一次。

代码实现

KMP的代码，网上有很多种写法，有和上面放的代码一样的while类型写法。

当然你也可以变一下，用for循环套while，效果是一样的。具体用哪个看你的选择。

下标从 $1$ 开始

#include<bits/stdc++.h>
#define N 1000010
using namespace std;
string a,b;
int n,m,nxt[N];
int main(){
	cin>>a>>b;
	n=a.size(),m=b.size();
	a=' '+a,b=' '+b;
	for(int i=2,j=1;i<=m;i++){
		while(b[i]!=b[j]&&j>1) j=nxt[j-1]+1;
		if(b[i]==b[j]) nxt[i]=j++;
	}
	for(int i=1,j=1;i<=n;i++){
		while(a[i]!=b[j]&&j>1) j=nxt[j-1]+1;
		if(a[i]==b[j]){
			if(j==m) cout<<i-j+1<<"\n";
			j++;
		}
	}
	for(int i=1;i<=m;i++) cout<<nxt[i]<<" ";
	return 0;
}

下标从 $0$ 开始

#include<bits/stdc++.h>
#define N 1000010
using namespace std;
string a,b;
int n,m,nxt[N];
int main(){
	cin>>a>>b;
	n=a.size(),m=b.size();
	for(int i=1,j=0;i<m;i++){
		while(b[i]!=b[j]&&j) j=nxt[j-1];
		if(b[i]==b[j]) nxt[i]=++j;
	}
	for(int i=0,j=0;i<n;i++){
		while(a[i]!=b[j]&&j) j=nxt[j-1];
		if(a[i]==b[j]){
			if(j==m-1) cout<<i-j+1<<"\n";
			j++;
		}
	}
	for(int i=0;i<m;i++) cout<<nxt[i]<<" ";
	return 0;
}

还有很多写法是把上面代码的 \(j\) 整体 \(-1\) 来使用，本质上是一样的，不过代码实现需要先j++才能得到与\(i\)匹配的位置。就不放代码了。

不同写法原理都是一样的，不要拘泥于细节，根据自己的习惯使用即可。

---

\(\mathcal{NEXT\ \ \ PHANTASM...}\)