[笔记]模意义下的乘法逆元
一些题目在涉及到超大整数运算时，往往会要求我们把答案取模一个值，比如\(998244353\)、\(10^9+7\)等等。如果我们的计算只有\(+,-,*\)，直接现算现取模即可：
(a + b) % mod = (a % mod + b % mod) % mod
(a - b) % mod = (a % mod - b % mod + 2 * mod) % mod
(a * b) % mod = (a % mod) * (b % mod) % mod
但如果遇到除法，我们就没法这么做了：
\(\frac{5}{3}*12\bmod 11=\ ?\)
\(\frac{10}{9}*81\bmod 13=\ ?\)
显然如果我们对分子和分母同时取\(\bmod\)是没用的，还可能出现结果不是整数的情况。
所以我们思考：在模\(p\)意义之下，如果能把\(\frac{a}{b}*c\)转化成\(a*x*c\)，而取模结果不变就好了。
这个\(x\)即为乘法运算中，模\(p\)意义下，\(b\)的逆元。
换句话说，\(x\)就是模\(p\)意义下\(b\)的倒数（也可写作\(b^{-1}\)），所以有
\(b*x\equiv 1\pmod p\)
所以我们要求\(b^{-1}\)，其实就是求满足上面这个式子的\(x\)。
举例：
\(\frac{5}{3}*12\bmod 11=\ 9\\
5*4*12\bmod 11=\ 9\)
（模\(11\)意义下\(3^{-1}=4\)）
\(\frac{10}{9}*81\bmod 13=\ 12\\
10*3*81\bmod 13=\ 12\)
（模\(13\)意义下\(9^{-1}=12\)）
具体求法共有\(3\)种：
- 费马小定理——\(O(\log\ p)\)，仅适用于\(p\)是质数。
- 扩展欧几里得——\(O(\log\ p)\)，适用于所有情况，即\((a,p)=1\)。
- 线性递推——\(O(p)\)求出\(1\sim p-1\)所有逆元，仅适用于\(p\)为质数。
- 附：递归求法
注意
- 模意义下乘法逆元在\([1,p-1]\)范围内有一个，\([-p+1,-1],[p+1,2p-1],[2p+1,3p-1]\)等等都各有一个（举例：\(3*2\equiv 3*7\equiv 3*12\equiv …\equiv 1\pmod 5\)）。但我们为了方便使用，一般都定义逆元在\([1,p-1]\)范围内，是唯一存在的。
- 模\(p\)意义下\(a^{-1}\)存在的充分必要条件是\((a,p)=1\)，即\(a,p\)互质。
所以，并不是\(p\)不为质数就没有逆元，也不是\(p\)为质数就一定存在逆元。（所以取模用的数不能随便选，绝大部分都是质数，比如$998244353$）证明
若$(a,p)\neq 1$，$a^{-1}*a\equiv 1\pmod p$显然不成立。
费马小定理
定理内容：如果\(p\)是质数，则对于所有\((a,p)=1\)，有\(a^{p-1}\equiv 1\pmod p\)。
注：\((a,b)\)表示\(a,b\)的最大公因数。
转化一下，\(a^{p-2}*a\equiv 1\pmod p\)。
这个形式很熟悉？没错，\(a^{p-2}\bmod p\)就是模\(p\)意义下\(a\)的逆元。
使用快速幂来求，时间复杂度\(O(\log p)\)。
注意：仅限于\(p\)为质数。
扩展欧几里得
扩展欧几里得算法本质上是辗转相除法（欧几里得算法）的扩展，其内容是：对于两个整数\(a,b\)，必有\(x,y\)使得\(ax+by=(a,b)\)。
怎么与逆元挂钩呢？我们设模\(p\)意义下\(a^{-1}=x\)，那么有\(a*x\equiv 1\pmod p\)，即\(ax=py+1\)，由于\(y\)可正可负，我们可以\(ax+py=1\)。刚才提到了^ 模\(p\)意义下\(a^{-1}\)存在的充分必要条件是\((a,p)=1\)，所以其实\(ax+py=(a,p)\)。满足扩展欧几里得的条件。
由于这是一个不定方程，所以会有多个解，我们前面提到过用最小的非负\(x\)作为逆元（^ 为了方便使用，一般都定义逆元在\([1,p-1]\)范围内，是唯一存在的）。
接下来我们解这个不定方程：
- 根据辗转相除法，\((a,p)=(p,a\bmod p)\)。
- 故一定存在\(ax_1+py_1=px_2+(a\bmod p)y_2\)。
- \(ax_1+py_1=px_2+(a-\lfloor \frac{a}{p}\rfloor p)y_2\)。
- \(\textcolor{magenta}{ax_1}+py_1=px_2+\textcolor{magenta}{ay_2}-\lfloor \frac{a}{p}\rfloor p y_2\)
- 那么，满足下列条件：\(\begin{cases} x_1=y_2\\ y_1=x_2-\lfloor \frac{a}{p}\rfloor y_2 \end{cases}\)的情况下，如果\(x_2,y_2\)满足要求，那么\(x_1,y_1\)一样也满足要求。
所以，我们可以通过不断递归调用求出我们想要的\(x_1,x_2\)。每次递归提供a,b,&x,&y。后两个参数只是引用，用于在上一层把结果进行转换（就是用上面的结论，把下一层计算的\(x_2,y_2\)，变成这一层的\(x_1,y_1\)）。a和b分别对应上面结论中的\(a,p\)。
递归结束条件和辗转相除法一样：\(b=0\)。
此时的\(a\)就是我们所求的\(\gcd\)。
因为\(ax+by=\gcd\)，所以\(x=1,y=0\)，这就是递归边界。
可以用下图帮助理解。
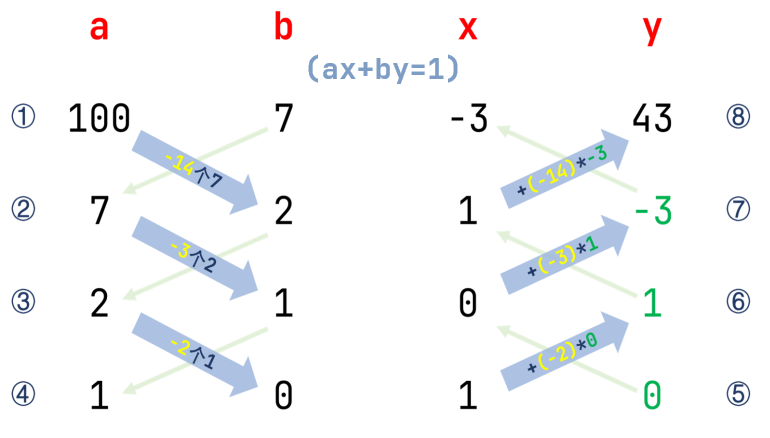
最终求出的\(x,y\)称为这个不定方程的特解，我们可以通过这个特解求出这个不定方程的通解（无穷多个）。虽然不在模除逆元的范畴，但是有必要一提。
这种已知特解求通解的方法适用于所有二元一次不定方程：
若存在\(ax+by=c\)，则可以根据特解\(x,y\)求出任意通解\(x',y'\)：
\(\begin{cases} x'=x+k*\frac{b}{\gcd(a,b)}\\ y'=y-k*\frac{a}{\gcd(a,b)} \end{cases}(k\in \mathbb{Z})\)
比如\(6*5+4*3=42\)，那么\(6*(5-2)+4*(3+3)=42\)等等，正确性显然。
注：经过大量样例测试，发现求出的通解\(x,y\)是有取值范围的：$x∈[-⌊\frac{p}{2}⌋,⌊\frac{p}{2}⌋]，y∈[-⌊\frac{a}{2}⌋,⌊\frac{a}{2}⌋] $，但是还不会证明，如果观众们有思路欢迎在评论区讨论。
时间复杂度：即辗转相除法的时间复杂度\(O(\log\ p)\)。
#include<bits/stdc++.h>
#define int long long
using namespace std;
int exgcd(int a,int b,int& x,int& y){
int d;
if(b==0) x=1,y=0,d=a;
else d=exgcd(b,a%b,y,x),y-=a/b*x;
return d;
}
signed main(){
int a,p,x,y;
cin>>a>>p;
exgcd(a,p,x,y);
cout<<(x%p+p)%p;
return 0;
}
之前代码放错了，抱歉www
线性递推
设\(k=\lfloor\frac{p}{i}\rfloor\)，\(p=ki+q\)。
\(
ki+q\equiv 0\pmod p\\
k*i*(i^{-1}*q^{-1})+q*(i^{-1}*q^{-1})\equiv 0\pmod p\\
k*q^{-1}+i^{-1}\equiv 0\pmod p\\
i^{-1}\equiv -k*q^{-1}\pmod p\\
i^{-1}\equiv -\lfloor\frac{p}{i}\rfloor*q^{-1}\pmod p\\
\)
按照上面的结论即可推得\(1\sim p-1\)的逆元。使用时调用\(inv[a]\)即可，如果\(a>p\)，那么需要调用\(inv[a\ mod\ p]\)。
时间复杂度\(O(n)\)。
例题：P3811 【模板】模意义下的乘法逆元
注意开long long，并且注意负数\(+p\)处理。
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,p,inv[3000010];
signed main(){
cin>>n>>p;
inv[1]=1;
cout<<inv[1]<<"\n";
for(int i=2;i<=n;i++){
inv[i]=(-p/i*inv[p%i]%p+p)%p;
cout<<inv[i]<<"\n";
}
return 0;
}
注意：仅适用于\(p\)为质数，否则存在\(p\bmod i=0\)，而\(0\)是不存在逆元的。
附：这种方法可以稍作修改，变成递归求逆元的代码。不用记忆化求单个数的逆元，目前时间复杂度未知，猜测为\(O(\log p)\)。具体见此知乎问题。
int inv(int a){
if(a==1) return 1;
return (-p/a*inv(p%a)%p+p)%p;
}
\(\textbf{[Fin.]}\)
\(\color{lightgray}\text{Next Dream...}\)
欢迎留下你的评论，我会认真阅读的！
