递归思想的巧妙理解

逻辑是数学的少年时代，数学是逻辑的成年时代。

——罗素

“递归”

这是在程序、算法设计中的基础和重中之重。当初理解这一点我也花费了不少时间，对于初学者来说，如何生动形象的展现着一过程，成了理解这一思想的关键。

这篇博文的来由，源于同学问我的一个问题：

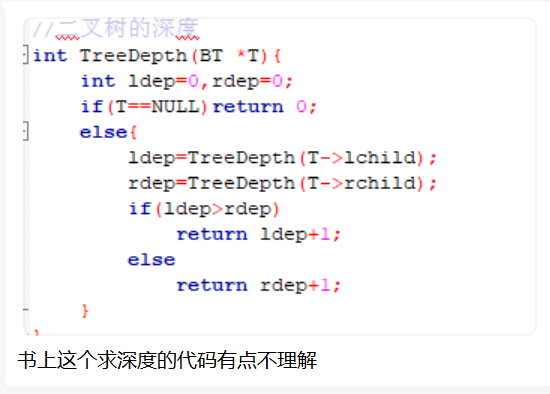
我一看啊，这波，这波是明显的递归啊！！

我想着，怎么解释呢，于是打开百度搜索递归：

定义

程序调用自身的编程技巧称为递归（ recursion）。递归做为一种算法在程序设计语言中广泛应用。 一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法，它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解，递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算，大大地减少了程序的代码量。递归的能力在于用有限的语句来定义对象的无限集合。一般来说，递归需要有边界条件、递归前进段和递归返回段。当边界条件不满足时，递归前进；当边界条件满足时，递归返回。

我想这，这么生硬的解释，还是别麻烦人家了吧，于是这个解释就鸽了好几天

奇思妙想

某个摸鱼的晚上，我突然想到了一个解释递归生动形象的例子，那就是：

俄罗斯套娃！！

那么，如何用俄罗斯套娃的思想去理解递归思想呢？

又是众所周知，递归其实就是程序调用自身，这不就好像是，在自己肚子里面装了一个自己么？

不过，我们开这个套娃的方式，得遵循以下规则；

 

先吧套娃的上半部分拿走（执行调用自身的函数上边的代码）；

继续拿上半部分，直到拿出了一个不能在开的娃（递归到底）；

看看这个不能再套娃的娃（完整的执行这个最“深”的函数）；

在依次拿出所有套娃的下半身（自底向上执行所有递归函数的下半部分）。

 

案例解释

我们先看这个求树的深度的代码：

int TreeDepth(BT *T){
    int ld=0,rd=0;
    if(T==NULL) return 0;
    else{
        ld=TreeDepth(T->lchild);
        rd=TreeDepth(T->rchild);
        if(ld>rd)
            return ld+1;
        else
            return rd+1;
    }
}

我就画个图来看看吧

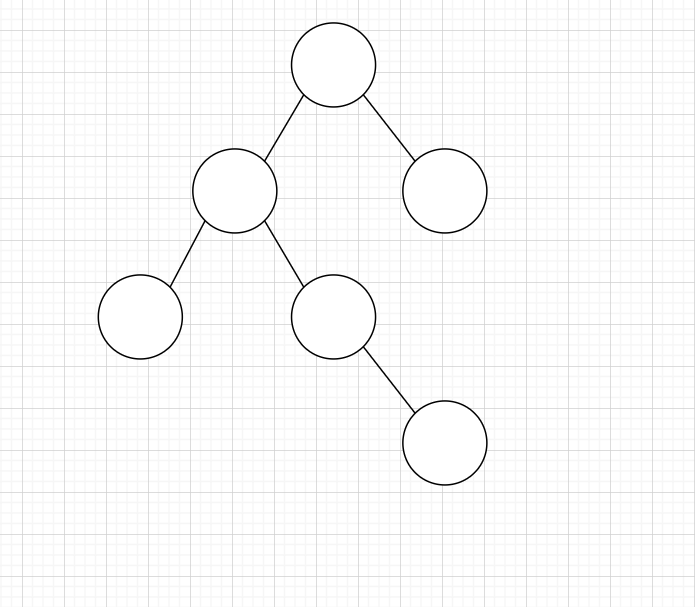
假设有这么一颗树，BT是函数中指针*T所在位置

我们执行这一段代码

int TreeDepth(BT *T){
    int ld=0,rd=0;
    if(T==NULL) return 0;
    else{
        ld=TreeDepth(T->lchild);

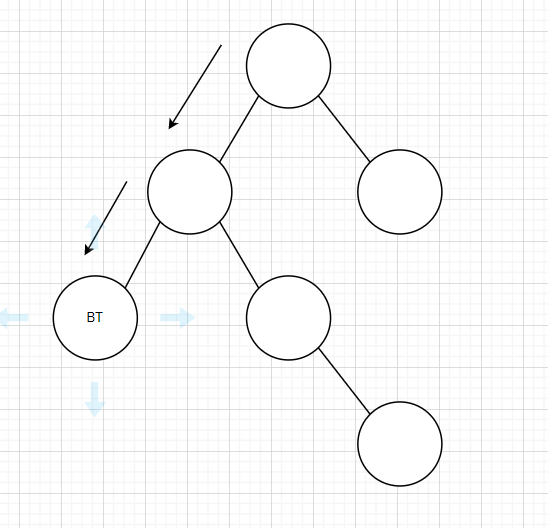
先递归到底边，在走下去，全是NULL了，就可以执行后一段代码

if(ld>rd)
            return ld+1;
        else
            return rd+1;

当然，这里ld和rd都是0，返回值是1，根据

ld=TreeDepth(T->lchild);

则上一层函数的ld=1

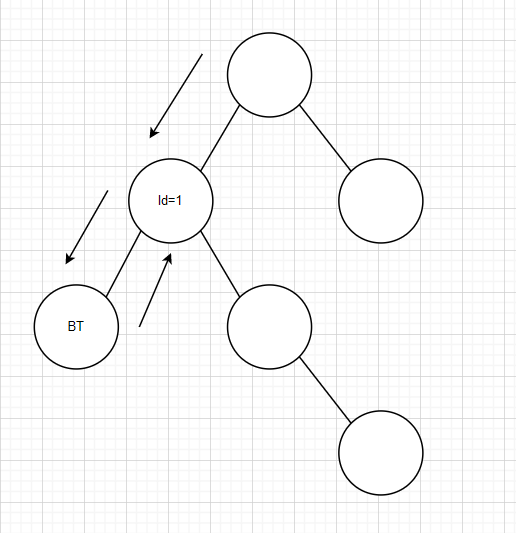
我们继续看，因为这一个函数已经执行结束了，我们来执行上一个函数的后半段代码。

       rd=TreeDepth(T->rchild);
        if(ld>rd)
            return ld+1;
        else
            return rd+1;
    }
}

这里我们发现，可以一直走右子树走下去，参考上一步的操作，以此类推，我们得到下图

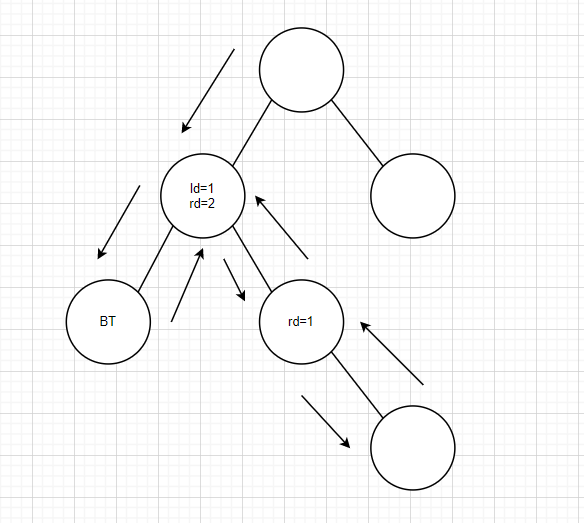
再继续推下去，整个程序的返回值就一目了然了

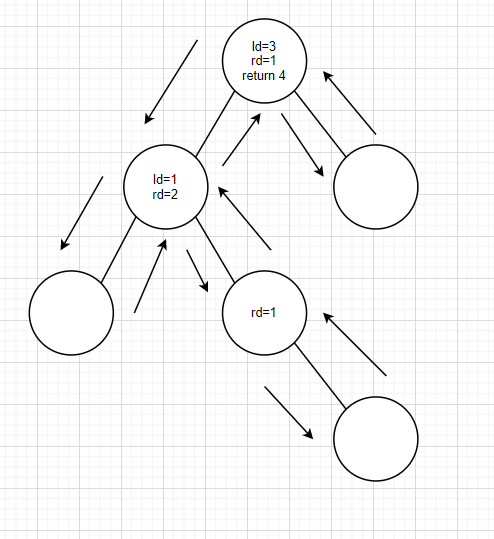
这里还是要再提一下深度优先搜索（DFS），众所周知深搜的最基本技巧就是递归。

PS：虽然深搜也可以用栈实现，不过递归就是程序自己调出栈来储存数据，差别不大。

树是特殊的图，树的遍历也是图的遍历，这种按照深度一口气遍历下来的方式，就是我们所谓的DFS，再树基础的学习过程中，我们也可以体会到很多图的性质

希望我的抛砖引玉能引起更多的思考😄