HDU 1560 DNA sequence(DNA序列)
HDU 1560 DNA sequence(DNA序列)
Time Limit: 15000/5000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Problem Description - 题目描述
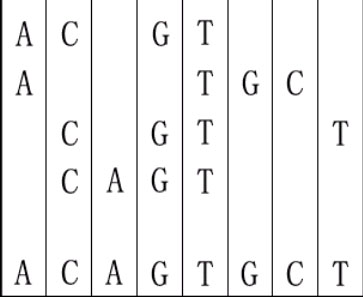
For example, given "ACGT","ATGC","CGTT" and "CAGT", you can make a sequence in the following way. It is the shortest but may be not the only one.

二十一世纪是生物技术突飞猛进的世纪。我们知道基因由DNA组成。构建DNA的核苷酸有A(腺嘌呤),C(胞嘧啶),G(鸟嘌呤)和T(胸腺嘧啶)。寻找DNA/蛋白质序列间的最长公共子序列是现代计算分子生物学的基本问题之一。然而这个问题有些许不同。给定若干DNA序列,你需要构建一个最短序列使得给定序列都是都是它的子序列。 比如。给定"ACGT","ATGC","CGTT"和"CAGT",你可以通过如下方式构建一个序列。最短序列不唯一。
The first line is the test case number t. Then t test cases follow.
In each case, the first line is an integer n ( 1<=n<=8 ) represents number of the DNA sequences.
The following k lines contain the k sequences, one per line. Assuming that the length of any sequence is between 1 and 5.

第一行为测试用例的数量t。随后t个测试用例。
每个用例中第一行为一个整数n ( 1<=n<=8 ) 表示DNA序列的数量。
随后k行,每行一个序列。假定任意序列长度为1到5。
Output - 输出
For each test case, print a line containing the length of the shortest sequence that can be made from these sequences.

对于每个测试用例,输出一行可构建序列的最短长度。
Sample Input - 输入样例
1 4 ACGT ATGC CGTT CAGT
Sample Output - 输出样例
8
题解
IDA* = (暴力DFS + 剪枝)*反反复复,所以问题在于怎么剪枝
如果用剩余待匹配序列的最大长度来剪枝……下面的数据就有问题(虽然HDU上并没有)
1 4 AAAA CCCC GGGG TTTT
然后秉着不会做就百度的原则(逃
横着看有问题,竖着看?
统计每行ACGT的个数,然后在以此求各个ACGT最大的和,依次剪枝就比上面的方法科学多了……
代码 C++
1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 int maxDeep, n, data[10][10]; 5 int vle(int(&siz)[10][4]) { 6 int i, j, opt, len[4]; 7 memset(len, 0, sizeof len); 8 for (i = 0; i < n; ++i) { 9 for (j = 0; j < 4; ++j) len[j] = std::max(len[j], siz[i][j]); 10 } 11 for (i = opt = 0; i < 4; opt += len[i++]); 12 return opt; 13 } 14 int DFS(int deep, int(&preW)[10], int(&preSiz)[10][4]) { 15 int i = vle(preSiz), j, w[10], siz[10][4], isFid; 16 if (!i) return 1; 17 if (i + deep > maxDeep) return 0; 18 for (i = 0; i < 4; ++i) { 19 memcpy(w, preW, sizeof w); memcpy(siz, preSiz, sizeof siz); 20 for (j = isFid = 0; j < n; ++j) { 21 if (data[j][w[j]] == i) { 22 isFid = ++w[j]; --siz[j][i]; 23 } 24 } 25 if (isFid && DFS(deep + 1, w, siz)) return 1; 26 } 27 return 0; 28 } 29 int main() { 30 int t, i, j, mp[300], w[10], siz[10][4]; 31 mp['A'] = 0; mp['C'] = 1; mp['G'] = 2; mp['T'] = 3; 32 memset(w, 0, sizeof w); 33 char str[10]; 34 scanf("%d", &t); 35 while (t--) { 36 memset(data, 0, sizeof data); memset(siz, 0, sizeof siz); 37 scanf("%d ", &n); 38 for (i = 0; i < n; ++i) { 39 gets(str); 40 for (j = 0; str[j]; ++j) ++siz[i][data[i][j] = mp[str[j]]]; 41 } 42 for (maxDeep = vle(siz); !DFS(0, w, siz); ++maxDeep); 43 printf("%d\n", maxDeep); 44 } 45 return 0; 46 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号