图论相关
1.最短路
引入
Dijkstra
Dijkstra 是基于贪心的一种算法,适用于非负权的图,求解单源最短路。
算法是这样的:
找出全局距离最小的点 \(u\),并用这个点去更新连接它的 \(v\) 点的距离。
时间复杂度 \(O(n^2)\),使用堆优化可以优化到 \(O(m \log m)\)
code
priority_queue<pi> Q;
void dij(LL u) {
memset(dis,63,sizeof dis);
memset(vis,0,sizeof vis);
dis[u]=0;
Q.push(mk(0,u));
for(; Q.size(); ) {
LL x=Q.top().second; Q.pop();
if(vis[x]) continue;
vis[x]=1;
for(LL i=0; i<(LL)e[x].size(); i++) {
LL y=e[x][i].first,z=e[x][i].second;
if(dis[y]>dis[x]+z) {
dis[y]=dis[x]+z; Q.push(mk(-dis[y],y));
}
}
}
}
Bellman_Ford
是一种可以处理负权的单源最短路算法。
算法是这样的:
枚举每条边,并更新这条边上点,称为一次松弛。
重复上诉操作直到没有点被更新。
如果经过了 \(n\) 轮松弛后还存在有点被更新,则原图存在负环。
时间复杂度 \(O(nm)\).
SPFA
SPFA 是 Bellman_Ford 的队列优化。
松弛节点 \(x\) 时找到接下来有可能松弛的点,
即与 \(x\) 相邻且最短路被更新的点压入队列。
判断负环只需要是否存在点判断进入队列是否超过 \(n-1\) 次。
若有,则有负环。
在一般图上效率很高,但是会被构造数据卡成 \(O(nm)\).
code
void spfa() {
memset(dis,63,sizeof dis);
Q.push(s),dis[s]=0;
for(; Q.size(); ) {
int x=Q.front(); Q.pop();
vis[x]=0;
for(int i=head[x]; i; i=nxt[i]) {
int y=ver[i],z=edge[i];
if(dis[y]>dis[x]+z) {
dis[y]=dis[x]+z;
if(++cnt[y]>=n) return puts("NO"),0;
if(!vis[y]) Q.push(y),vis[y]=1;
}
}
}
}
应用
P5304 [GXOI/GZOI2019] 旅行者
如果我们设最短的最短路的两个点为 \(u,v\).
设 \(u\),\(v\) 在两个不同的部分。
那么我们只要建立一个起点 \(s\),向 \(u\) 部分建长度为 \(0\) 的边。
再建立一个终点 \(t\),让 \(v\) 的部分向 \(t\) 建长度为 \(0\) 的边。
\(s\rightarrow t\) 最短路即为 \(u\) 部分任一点到 \(v\) 部分任一点的最小值。
那么我们考虑将点分组。
可以随机分,设分 \(k\) 次,正确率是 \(1-(\frac{3}{4})^k\).
时间复杂度是 \(O(k\cdot m\log m)\).
code
#include<bits/stdc++.h>
#define pi pair<LL,LL>
#define mk make_pair
using namespace std;
using LL=long long;
const LL N=1e5+10,M=5e5+10;
const LL Rd=23;
LL T,n,m,k,e1,e2,t[N],p[N],dis[N];
bool vis[N];
vector<pi> e[N];
void init() {
for(LL i=1; i<=n; i++) e[i].clear();
}
void addedge(LL u,LL v,LL w) {
e[u].push_back(mk(v,w));
}
priority_queue<pi> Q;
void dij(LL u) {
memset(dis,63,sizeof dis);
memset(vis,0,sizeof vis);
dis[u]=0;
Q.push(mk(0,u));
for(; Q.size(); ) {
LL x=Q.top().second; Q.pop();
if(vis[x]) continue;
vis[x]=1;
for(LL i=0; i<(LL)e[x].size(); i++) {
LL y=e[x][i].first,z=e[x][i].second;
if(dis[y]>dis[x]+z) {
dis[y]=dis[x]+z; Q.push(mk(-dis[y],y));
}
}
}
}
void solve() {
init();
scanf("%lld%lld%lld",&n,&m,&k);
for(LL i=1,u,v,w; i<=m; i++) {
scanf("%lld%lld%lld",&u,&v,&w);
addedge(u,v,w);
}
for(LL i=1; i<=k; i++) scanf("%lld",&t[i]);
e1=n+1; e2=n+2;
for(LL i=1; i<=k; i++) p[i]=t[i];
LL ans=1e18;
for(LL o=1; o<=Rd; o++) {
random_shuffle(p+1,p+1+k);
for(LL i=1; i<=k/2; i++)
addedge(e1,p[i],0);
for(LL i=k/2+1; i<=k; i++)
addedge(p[i],e2,0);
dij(e1);
ans=min(ans,dis[e2]);
e[e1].clear();
for(LL i=k/2+1; i<=k; i++) {
e[p[i]].erase(--e[p[i]].end());
}
}
printf("%lld\n",ans);
}
signed main() {
srand(1919);
scanf("%lld",&T);
for(; T; T--) solve();
return 0;
}
正解是二进制分组,每次编号二进制第 \(i\) 为 \(0\) 的分左边,为 \(1\) 的分右边。
P1266 速度限制
是分层图最短路。
即状态多加了一维。
可以看做第二维状态是不同的层。
每个层都是一个图。
层与层直接有联系。
整体上还是用 dijkstra 算法。
code
#include<bits/stdc++.h>
using namespace std;
const int N=155,M=24005,K=505;
int head[N],tot,nxt[M],ver[M],len[M],spd[M];
int pre[N][K][2];
double dis[N][K];
bool vis[N][K];
int n,m,d;
int tp,st[N];
struct node {
int u,s;
double t;
bool operator < (const node A) const {return t>A.t;}
node() {}
node(int u_,int s_,double t_) {u=u_; s=s_; t=t_;}
} ;
priority_queue<node> Q;
void addedge(int u,int v,int w,int z) {
ver[++tot]=v; nxt[tot]=head[u];
spd[tot]=w; len[tot]=z;
head[u]=tot;
}
void dij() {
for(int i=0; i<=n; i++) for(int j=0; j<K; j++) dis[i][j]=1e18;
pre[1][70][0]=-1;
dis[1][70]=0;
Q.push(node(1,70,dis[1][70]));
for(; Q.size(); ) {
int u=Q.top().u,s=Q.top().s;
Q.pop();
if(vis[u][s]) continue;
vis[u][s]=1;
for(int i=head[u]; i; i=nxt[i]) {
int v=ver[i];
if(spd[i]!=0) {
if(dis[v][spd[i]]>dis[u][s]+1.0*len[i]/spd[i]) {
dis[v][spd[i]]=dis[u][s]+1.0*len[i]/spd[i];
pre[v][spd[i]][0]=u; pre[v][spd[i]][1]=s;
Q.push(node(v,spd[i],dis[v][spd[i]]));
}
} else {
if(dis[v][s]>dis[u][s]+1.0*len[i]/s) {
dis[v][s]=dis[u][s]+1.0*len[i]/s;
pre[v][s][0]=u; pre[v][s][1]=s;
Q.push(node(v,s,dis[v][s]));
}
}
}
}
int idx=0;
for(int i=1; i<K; i++) {
if(dis[d][i]<dis[d][idx]) idx=i;
}
for(int u=d,i=idx; ; ) {
st[++tp]=u;
int v=u,j=i;
if(pre[v][j][0]==-1) break;
u=pre[v][j][0]; i=pre[v][j][1];
}
for(int i=tp; i>=1; i--) printf("%d ",st[i]-1);
puts("");
}
int main() {
scanf("%d%d%d",&n,&m,&d); d++;
for(int i=1,u,v,w,z; i<=m; i++) {
scanf("%d%d%d%d",&u,&v,&w,&z);
u++; v++; addedge(u,v,w,z);
}
dij();
return 0;
}
2.差分约束
引入
解决不定方程组,类似这样。
\( \begin{cases} x_2 \le x_1 -1 \\ x_3 \le x_1 +3 \\ x_3 \le x_2 +2 \end{cases} \)
我们发现这有点像三角形不等式,即求解完最短路后每条边满足的性质。
注:最短路的三角形不等式,即对于边 \(u\rightarrow v\),有 \(dis_v\le dis_u+w_{u,v}\),否则可以继续更新。
则我们建一个图:
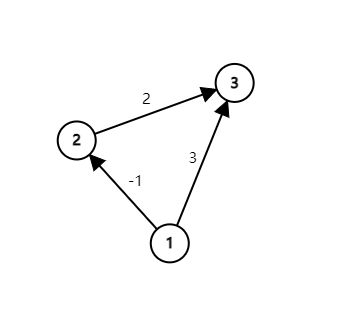
\(d_1=0,d_2=-1,d_3=1\)
我们发现,这样求出来是对的。
不过,为了防止图不连通,我们建立源点,并向所有点连一条长 \(0\) 的边。
如果出现负环,那么就无解。
用 SPFA.
有一点技巧,若出现 \(x_1=x_2+1\) 这类等号,则等于 \(x_1 \le x_2+1\),且 \(x_1 \ge x_2+1\).
code
#include<bits/stdc++.h>
using namespace std;
const int N=5e3+10;
int head[N],ver[N],nxt[N],edge[N],tot;
int n,m,cnt[N],dis[N];
bool vis[N];
queue<int> Q;
void addedge(int x,int y,int z) {
ver[++tot]=y; edge[tot]=z;
nxt[tot]=head[x]; head[x]=tot;
}
int main() {
scanf("%d%d",&n,&m);
for(int i=1,x1,x2,y; i<=m; i++) {
scanf("%d%d%d",&x1,&x2,&y);
addedge(x2,x1,y);
}
for(int i=1; i<=n; i++) Q.push(i),vis[i]=1,dis[i]=0;
for(; Q.size(); ) {
int x=Q.front(); Q.pop();
vis[x]=0;
for(int i=head[x]; i; i=nxt[i]) {
int y=ver[i],z=edge[i];
if(dis[y]>dis[x]+z) {
dis[y]=dis[x]+z;
if(++cnt[y]>=n) return puts("NO"),0;
if(!vis[y]) Q.push(y),vis[y]=1;
}
}
}
for(int i=1; i<=n; i++) printf("%d ",dis[i]);
puts("");
return 0;
}
应用
UVA1723 Intervals
考虑前缀和,然后列出一些关系。
由于求最小解,那么用最长路求(笔者也不会证)。
code
#include<bits/stdc++.h>
using namespace std;
const int N=50010,M=2e5+10;
int t,k,n;
int head[N],tot,nxt[M],ver[M],edge[M];
int dis[N],vis[N];
void addedge(int x,int y,int z) {
ver[++tot]=y;
nxt[tot]=head[x];
edge[tot]=z;
head[x]=tot;
}
queue<int> Q;
void solve() {
memset(head,0,sizeof head); tot=0;
scanf("%d",&k);
n=0;
for(int i=1,a,b,c; i<=k; i++) {
scanf("%d%d%d",&a,&b,&c);
addedge(a,b+1,c);
n=max(n,b);
}
for(int i=1; i<=n+1; i++) addedge(i-1,i,0);
for(int i=1; i<=n+1; i++) addedge(i,i-1,-1);
for(int i=0; i<=n+1; i++) dis[i]=-1e9;
dis[0]=0; vis[0]=1; Q.push(0);
for(; Q.size(); ) {
int x=Q.front(); Q.pop();
vis[x]=0;
for(int i=head[x]; i; i=nxt[i]) {
int y=ver[i],z=edge[i];
if(dis[y]<dis[x]+z) {
dis[y]=dis[x]+z;
if(!vis[y]) vis[y]=1,Q.push(y);
}
}
}
printf("%d\n",dis[n+1]);
}
int main() {
scanf("%d",&t);
for(; t; t--) {
solve();
if(t!=1) puts("");
}
return 0;
}
P5590 赛车游戏
使得每条路径相同,条件是对于每条边 \(u\rightarrow v\),\(dis_v=dis_u+w_{u,v}\)
又因 \(1\le w_{u,v}\le 9\),那么转化为 \(dis_v \le dis_u+9,dis_v \ge dis_u+1\).
差分约束求解即可。
code
#include<bits/stdc++.h>
using namespace std;
const int N=1e3+10,M=2e3+10;
int n,m,vis[N],dis[N],cnt[N];
int head[N],from[M],nxt[M],ver[M],tot,val[N],viz[N];
vector<pair<int,int>> e[N];
queue<int> Q;
void addedge(int x,int y) {
ver[++tot]=y; from[tot]=x;
nxt[tot]=head[x]; head[x]=tot;
}
void aDD(int u,int v) {
e[v].push_back(make_pair(u,-1));
e[u].push_back(make_pair(v,9));
}
int dfs(int u) {
viz[u]=1;
if(val[u]||u==n) return val[u]=1;
for(int i=head[u]; i; i=nxt[i]) {
int v=ver[i];
if(val[v]) aDD(u,v),val[u]=1;
else if(!viz[v]&&dfs(v)) aDD(u,v),val[u]=1;
}
return val[u];
}
int main() {
scanf("%d%d",&n,&m);
for(int i=1,u,v; i<=m; i++) {
scanf("%d%d",&u,&v);
addedge(u,v);
}
if(!dfs(1)) return puts("-1"),0;
for(int i=1; i<=n; i++) vis[i]=1,Q.push(i),dis[i]=0;
for(; Q.size(); ) {
int x=Q.front(); Q.pop();
vis[x]=0;
for(int j=0; j<(int)e[x].size(); j++) {
int y=e[x][j].first,z=e[x][j].second;
if(dis[y]>dis[x]+z) {
dis[y]=dis[x]+z;
if(++cnt[y]>=n) return puts("-1"),0;
if(!vis[y]) vis[y]=1,Q.push(y);
}
}
}
printf("%d %d\n",n,m);
for(int i=1; i<=m; i++) {
int d=dis[ver[i]]-dis[from[i]];
printf("%d %d %d\n",from[i],ver[i],(d<1||d>9)?1:d);
}
return 0;
}
P4926 [1007] 倍杀测量者
注意到“有人女装”即为存在负环。
二分判断即可。
code
#include<bits/stdc++.h>
using namespace std;
const double eps=1e-8;
const int N=1050;
struct flag{int o,a,b,k;} fl[N];
struct edge{int next,to; double w;} a[N<<1];
int n,s,t,c[N],fr[N],head[N],cnt,vis[N];
double dis[N];
queue<int> Q;
void link(int x,int y,double w) {a[++cnt]=(edge){head[x],y,w};head[x]=cnt;}
int check(double T) {
memset(head,0,sizeof(head));
memset(fr,0,sizeof(fr));cnt=0;
while(!Q.empty()) Q.pop();
for(int i=0; i<=n; i++) dis[i]=1,fr[i]=0,vis[i]=1,Q.push(i);
for(int i=1; i<=n; i++)
if(c[i]) link(i,0,1.0/c[i]),link(0,i,c[i]);
for(int i=1; i<=s; i++) {
int A=fl[i].a,B=fl[i].b,k=fl[i].k,o=fl[i].o;
if(o==1) link(B,A,k-T);
else link(B,A,1.0/(k+T));
}
while(!Q.empty()) {
int x=Q.front();
for(int i=head[x]; i; i=a[i].next) {
int R=a[i].to;
if(dis[R]>=dis[x]*a[i].w) continue;
dis[R]=dis[x]*a[i].w;fr[R]=fr[x]+1;
if(fr[R]==n+2) return 1;
if(!vis[R]) Q.push(R),vis[R]=1;
}
Q.pop(); vis[x]=0;
}
return 0;
}
int main(){
cin>>n>>s>>t;
double l=0,r=1e18,T=-1;
for(int i=1; i<=s; i++) {
int o,a,b,k;
cin>>o>>a>>b>>k;
fl[i]=(flag){o,a,b,k};
if(o==1) r=min(r,(double)k-eps);
}
for(int i=1,C,x; i<=t; i++) cin>>C>>x,c[C]=x;
while(r-l>eps) {
double mid=(l+r)/2;
check(mid)?l=T=mid:r=mid;
}
T==-1?puts("-1"):printf("%.10lf\n",T);
return 0;
}
3.生成树
引入
kruscal
贪心,先将所有边按权从小到大排序,然后一一尝试加入。
若两点不连通,则加入。这里可以用并查集维护。
应用
P1967 [NOIP2013 提高组] 货车运输
跑最大生成树,然后树上倍增判断一下。
code
#include<bits/stdc++.h>
using namespace std;
const int N=1e4+10,logn=15,M=5e4+10;
int n,m,q,fa[N],f[N][logn],g[N][logn],depth[N];
int s[N];
struct node {
int u,v,w;
} e[M];
int tot,head[N],ver[2*N],nxt[2*N],edge[2*N];
int getf(int x) {
if(x==fa[x]) return x;
else return fa[x]=getf(fa[x]);
}
bool cmp(node p,node q) {
return p.w>q.w;
}
void addedge(int x,int y,int z) {
ver[++tot]=y;
edge[tot]=z;
nxt[tot]=head[x];
head[x]=tot;
}
void dfs(int u,int z,int father) {
depth[u]=depth[father]+1;
f[u][0]=father; g[u][0]=z;
for(int i=1; i<logn; i++) f[u][i]=f[f[u][i-1]][i-1];
for(int i=1; i<logn; i++) g[u][i]=min(g[u][i-1],g[f[u][i-1]][i-1]);
for(int i=head[u]; i; i=nxt[i]) {
int v=ver[i],z=edge[i];
if(v==father) continue;
dfs(v,z,u);
}
}
int Lca(int u,int v) {
int ans=1e9;
if(depth[u]<depth[v]) swap(u,v);
for(int i=logn-1; i>=0; i--) {
if(depth[f[u][i]]>=depth[v]) {
ans=min(ans,g[u][i]);
u=f[u][i];
}
}
if(u==v) return ans;
for(int i=logn-1; i>=0; i--) {
if(f[u][i]!=f[v][i]) {
ans=min(ans,min(g[u][i],g[v][i]));
u=f[u][i]; v=f[v][i];
}
}
if(u!=v) ans=min(ans,min(g[u][0],g[v][0]));
return ans;
}
int main() {
scanf("%d%d",&n,&m);
memset(g,127,sizeof(g));
for(int i=1; i<=m; i++) scanf("%d%d%d",&e[i].u,&e[i].v,&e[i].w);
sort(e+1,e+1+m,cmp);
for(int i=1; i<=n; i++) fa[i]=i;
for(int i=1; i<=m; i++) {
int fx=getf(e[i].u),fy=getf(e[i].v);
if(fx!=fy) {
addedge(e[i].u,e[i].v,e[i].w);
addedge(e[i].v,e[i].u,e[i].w);
fa[fx]=fy;
}
}
for(int i=1; i<=n; i++) {
fa[i]=getf(fa[i]);
if(s[fa[i]]) continue;
dfs(fa[i],1e9,0);
s[fa[i]]=1;
}
scanf("%d",&q);
for(int u,v; q; q--) {
scanf("%d%d",&u,&v);
if(fa[u]!=fa[v]) printf("-1\n");
else {
printf("%d\n",Lca(u,v));
}
}
return 0;
}
4.连通性问题
引入
5.2-sat
引入
用于解决布尔方程组。
\(
\begin{cases}
p \wedge q = 1\\
p \wedge \neg q = 1
\end{cases}
\)
如上面这个例子。
我们将一个点拆成两个点,对应取值为 \(0\) 或 \(1\).
因为 \(p \wedge q = 1\) ,把 \(p_0\) 向 \(q_1\) 建边,把 \(q_0\) 向 \(p_1\) 建边。
因为 $p \wedge \neg q = 1 $,把 \(p_0\) 向 \(q_0\) 建边,把 \(q_1\) 向 \(p_0\) 建边。
建边 \(u\rightarrow v\) 的意思是如果有 \(u\) ,则 \(v\).
然后求解强连通分量。
若存在 \(p_0,p_1\) 在同一分量,那么无解。
如果有解,如何输出方案呢?
先拓扑排序,容易发现拓扑序较大的是最后取值,即存在 \(p(较小)\) 到 \(p(较大)\) 的路径。
所以 \(p(较小)\) 能推出 \(p(较大)\)。
所以对于 \(p_0,p_1\) 选择拓扑序较大那个。
对点编号可以用 \(i\),\(i+n\) 编号。
code
#include<bits/stdc++.h>
using namespace std;
const int N=2e6+10;
int n,k;
int head[N],ver[N],nxt[N],tot;
int dfn[N],low[N],num,stk[N],ins[N],tp,c[N],scc;
void addedge(int x,int y) {
ver[++tot]=y; nxt[tot]=head[x]; head[x]=tot;
}
void tarjan(int u) {
dfn[u]=low[u]=++num;
stk[++tp]=u; ins[u]=1;
for(int i=head[u]; i; i=nxt[i]) {
int v=ver[i];
if(!dfn[v]) {
tarjan(v);
low[u]=min(low[u],low[v]);
} else if(ins[v]) {
low[u]=min(low[u],dfn[v]);
}
}
if(low[u]==dfn[u]) {
scc++; int v;
do {
v=stk[tp--]; ins[v]=0;
c[v]=scc;
} while(u!=v);
}
}
int main() {
scanf("%d%d",&n,&k);
for(int i=1,u,a,v,b; i<=k; i++) {
scanf("%d%d%d%d",&u,&a,&v,&b);
addedge(u+(a^1)*n,v+b*n);
addedge(v+(b^1)*n,u+a*n);
}
for(int i=1; i<=2*n; i++)
if(!dfn[i]) tarjan(i);
for(int i=1; i<=n; i++)
if(c[i]==c[i+n]) return puts("IMPOSSIBLE"),0;
puts("POSSIBLE");
for(int i=1; i<=n; i++) {
putchar(c[i+n]<c[i]?'1':'0');
putchar(' ');
}
return 0;
}
应用
P3825 [NOI2017] 游戏
注意到如果没有 \(x\) 就是裸 2-sat.
那么枚举 \(x\) 的取值,注意这里不需要 abc 都枚举,只用枚举 ab,因为已经涵盖所有情况了。
code
#include<bits/stdc++.h>
using namespace std;
const int N=4e5+10;
int n,d,k;
int p[30],cnt;
char s[N];
struct node {
int u,a,v,b;
} r[N];
int head[N],nxt[N],ver[N],tot;
void addedge(int x,int y) {
ver[++tot]=y;
nxt[tot]=head[x];
head[x]=tot;
}
int dfn[N],low[N],num,st[N],tp,ins[N],c[N],dcc;
void tarjan(int u) {
dfn[u]=low[u]=++num;
st[++tp]=u; ins[u]=1;
for(int i=head[u]; i; i=nxt[i]) {
int v=ver[i];
if(!dfn[v]) {
tarjan(v); low[u]=min(low[u],low[v]);
} else if(ins[v]) {
low[u]=min(low[u],dfn[v]);
}
}
if(dfn[u]==low[u]) {
++dcc; int v;
do {
v=st[tp--]; c[v]=dcc;
ins[v]=0;
} while(u!=v);
}
}
bool solve() {
memset(head,0,sizeof head); tot=0;
for(int i=1; i<=k; i++) {
int u=r[i].u,v=r[i].v;
int a=-1,b=-1;
if(s[u]=='a') {
if(r[i].a==1) a=0; else if(r[i].a==2) a=1;
} else if(s[u]=='b') {
if(r[i].a==0) a=0; else if(r[i].a==2) a=1;
} else if(s[u]=='c') {
if(r[i].a==0) a=0; else if(r[i].a==1) a=1;
}
if(s[v]=='a') {
if(r[i].b==1) b=0; else if(r[i].b==2) b=1;
} else if(s[v]=='b') {
if(r[i].b==0) b=0; else if(r[i].b==2) b=1;
} else if(s[v]=='c') {
if(r[i].b==0) b=0; else if(r[i].b==1) b=1;
}
if(a==-1) continue;
if(b==-1) {
addedge(a*n+u,(a^1)*n+u);
continue;
}
addedge(a*n+u,b*n+v);
addedge((b^1)*n+v,(a^1)*n+u);
}
memset(dfn,0,sizeof dfn); num=0;
for(int i=1; i<=2*n; i++)
if(!dfn[i]) tarjan(i);
for(int i=1; i<=n; i++)
if(c[i]==c[i+n]) return false;
for(int i=1; i<=n; i++) {
if(s[i]=='a') putchar(c[i]<c[i+n]?'B':'C');
else if(s[i]=='b') putchar(c[i]<c[i+n]?'A':'C');
else if(s[i]=='c') putchar(c[i]<c[i+n]?'A':'B');
}
return true;
}
int main() {
scanf("%d%d",&n,&d);
scanf("%s",s+1);
for(int i=1; i<=n; i++)
if(s[i]=='x') p[cnt++]=i;
scanf("%d",&k);
for(int i=1; i<=k; i++) {
char a,b; int u,v;
scanf("%d %c %d %c",&u,&a,&v,&b);
r[i]={u,a-'A',v,b-'A'};
}
for(int mask=0; mask<(1<<d); mask++) {
for(int i=0; i<d; i++) {
if(mask&(1<<i)) s[p[i]]='a';
else s[p[i]]='b';
}
if(solve()) return 0;
}
puts("-1");
return 0;
}
P6378 [PA2010] Riddle
2-sat 考的就是建图。
每个部分用一下前缀优化建图。
先拆点,然后这样。

code
#include<bits/stdc++.h>
using namespace std;
const int N=8e6+10;
int n,m,k;
int head[N],ver[N],nxt[N],tot;
int a[N];
void addedge(int x,int y) {
ver[++tot]=y;
nxt[tot]=head[x];
head[x]=tot;
}
int dfn[N],low[N],num,st[N],tp,ins[N],c[N],dcc;
void tarjan(int u) {
dfn[u]=low[u]=++num;
st[++tp]=u; ins[u]=1;
for(int i=head[u]; i; i=nxt[i]) {
int v=ver[i];
if(!dfn[v]) {
tarjan(v); low[u]=min(low[u],low[v]);
} else if(ins[v]) {
low[u]=min(low[u],dfn[v]);
}
}
if(dfn[u]==low[u]) {
++dcc; int v;
do {
v=st[tp--]; c[v]=dcc;
ins[v]=0;
} while(u!=v);
}
}
int main() {
scanf("%d%d%d",&n,&m,&k);
for(int i=1,u,v; i<=m; i++) {
scanf("%d%d",&u,&v);
addedge(u,v+n); addedge(v,u+n);
}
for(int i=1,w; i<=k; i++) {
scanf("%d",&w);
for(int i=1; i<=w; i++) scanf("%d",&a[i]);
for(int i=1; i<=w; i++) {
addedge(a[i]+n,a[i]+3*n);
addedge(a[i]+2*n,a[i]);
}
for(int i=1; i<w; i++) {
addedge(a[i]+3*n,a[i+1]);
addedge(a[i+1]+n,a[i]+2*n);
addedge(a[i]+3*n,a[i+1]+3*n);
addedge(a[i+1]+2*n,a[i]+2*n);
}
}
for(int i=1; i<=2*n; i++) if(!dfn[i]) tarjan(i);
for(int i=1; i<=n; i++) if(c[i]==c[i+n]) return puts("NIE"),0;
return puts("TAK"),0;
}
[ARC069F] Flags
二分 \(d\).
然后对于每个点,对其他距离小于 \(d\) 的点的另一个点建边。
这里可以用 ds 优化建图。
我用了分块。
code
#include<bits/stdc++.h>
using namespace std;
const int N=4e4+10,M=12e6+10;
int n,cnt;
int blk,bl[N],L[N],R[N],bo[N],opp[N];
struct node {
int pos,id;
bool operator < (const node s) const {
return pos<s.pos;
}
} p[N];
int head[N],ver[M],nxt[M],tot;
void addedge(int x,int y) {
ver[++tot]=y; nxt[tot]=head[x]; head[x]=tot;
}
int dfn[N],low[N],num,st[N],tp,ins[N],c[N],dcc;
void tarjan(int u) {
dfn[u]=low[u]=++num;
st[++tp]=u; ins[u]=1;
for(int i=head[u]; i; i=nxt[i]) {
int v=ver[i];
if(!dfn[v]) {
tarjan(v); low[u]=min(low[u],low[v]);
} else if(ins[v]) {
low[u]=min(low[u],dfn[v]);
}
}
if(dfn[u]==low[u]) {
++dcc; int v;
do {
v=st[tp--]; c[v]=dcc;
ins[v]=0;
} while(u!=v);
}
}
bool cmp(node x,node y) {
return x.pos<y.pos;
}
void Link(int x,int l,int r) {
if(l>r) return ;
if(bl[l]==bl[r]) {
for(int i=l; i<=r; i++) addedge(x,opp[p[i].id]);
return ;
}
int Bl=bl[l],Br=bl[r];
for(int i=Bl+1; i<=Br-1; i++) addedge(x,bo[i]);
for(int i=l; i<=R[Bl]; i++) addedge(x,opp[p[i].id]);
for(int i=L[Br]; i<=r; i++) addedge(x,opp[p[i].id]);
}
bool valid(int dis) {
memset(head,0,sizeof head); tot=0;
for(int i=1; i<=bl[2*n]; i++) {
bo[i]=cnt+i;
for(int j=L[i]; j<=R[i]; j++)
addedge(bo[i],opp[p[j].id]);
}
for(int i=1; i<=2*n; i++) {
int l_=upper_bound(p+1,p+1+cnt,node{p[i].pos-dis,0})-p;
int r_=upper_bound(p+1,p+1+cnt,node{p[i].pos+dis-1,0})-p-1;
Link(p[i].id,l_,i-1); Link(p[i].id,i+1,r_);
}
memset(dfn,0,sizeof dfn); num=dcc=0;
for(int i=1; i<=2*n; i++) if(!dfn[i]) tarjan(i);
for(int i=1; i<=n; i++) if(c[i]==c[opp[i]]) return false;
return true;
}
int main() {
scanf("%d",&n); blk=sqrt(n+10);
for(int i=1,a,b; i<=n; i++) {
scanf("%d%d",&a,&b);
p[++cnt]={a,i}; p[++cnt]={b,n+i};
opp[i]=n+i; opp[n+i]=i;
}
sort(p+1,p+1+cnt,cmp);
for(int i=1; i<=2*n; i++) {
bl[i]=i/blk+1;
if(!L[bl[i]]) L[bl[i]]=i;
R[bl[i]]=max(R[bl[i]],i);
}
int l=0,r=1061109567,ans=0;
while(l<=r) {
int mid=(l+r)/2;
if(valid(mid)) l=mid+1,ans=mid;
else r=mid-1;
}
printf("%d\n",ans);
return 0;
}
6.网络流
引入
7.点分治
引入
8.基环树
引入
基环树是一棵树加上一条边。
常见的维护手法是把环和非环分开讨论、把环缩点、断开环上边计算。
应用
P1453 城市环路
若是一颗树,可以树形 Dp。
先找环,然后环上每个点分别树形 Dp。
再断环成链,做一个环形 Dp。
设环有 \(m\) 个点。
钦定第一个点选,那么第 \(m\) 个点不选。
钦定第 \(m\) 个点选,那么第一个点不选。
code
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n,p[N],head[N],nxt[N<<1],ver[N<<1],tot;
double k;
void addedge(int x,int y) {
ver[++tot]=y,nxt[tot]=head[x],head[x]=tot;
}
int vis[N];
int c[N],cnt;
int f[N][2],g[N][2],ans;
int findloop(int u,int fa) {
if(vis[u]) return u;
vis[u]=1;
for(int i=head[u]; i; i=nxt[i]) {
int v=ver[i];
if(v==fa) continue;
int suf=findloop(v,u);
if(suf) {
c[++cnt]=u; vis[u]=2;
return suf==u?0:suf;
}
}
return 0;
}
void solve(int u,int fa) {
f[u][1]=p[u],f[u][0]=0;
for(int i=head[u]; i; i=nxt[i]) {
int v=ver[i];
if(vis[v]==2||v==fa) continue;
solve(v,u);
f[u][1]+=f[v][0];
f[u][0]+=max(f[v][0],f[v][1]);
}
}
int main() {
scanf("%d",&n);
for(int i=1; i<=n; i++) scanf("%d",&p[i]);
for(int i=1,u,v; i<=n; i++) {
scanf("%d%d",&u,&v); u++,v++;
addedge(u,v),addedge(v,u);
}
scanf("%lf",&k);
findloop(1,1);
for(int i=1; i<=cnt; i++) {
solve(c[i],c[i]);
}
g[1][0]=f[c[1]][0],g[1][1]=-1e9;
for(int i=2; i<=cnt; i++) {
g[i][1]=g[i-1][0]+f[c[i]][1];
g[i][0]=max(g[i-1][0],g[i-1][1])+f[c[i]][0];
}
ans=max(g[cnt][0],g[cnt][1]);
g[1][0]=f[c[1]][0],g[1][1]=f[c[1]][1];
for(int i=2; i<=cnt; i++) {
g[i][1]=g[i-1][0]+f[c[i]][1];
g[i][0]=max(g[i-1][0],g[i-1][1])+f[c[i]][0];
}
ans=max(ans,g[cnt][0]);
printf("%.1lf\n",ans*k);
return 0;
}
P4381 [IOI2008] Island
求基环树直径。
设环上有 \(m\) 个点。
设 \(d_i\) 为环上 \(i\) 子树距离 \(i\) 最远距离。
\(\max(d_i+d_j+dis(i,j))\)
\(dis(i,j)\) 可以用前缀和。
破坏成链,并把链加倍,即在 \([m+1,2m]\) 复制一遍。
计算出 \(s\) 为距离前缀和。
答案即为 \((d_i+s_i) + (d_j-s_j)\),其中 \(i-j<m\).
单调队列即可。
最后还要考虑环上子树中的直径。
code
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=2e6+10;
int n,y,z,tot=1,head[N],nxt[N],ver[N];
LL edge[N],w,dl[N],dis[N],f[N],s[N],ret;
int c[N],m,vis[N],is[N];
void addedge(int x,int y,LL z) {
ver[++tot]=y;
nxt[tot]=head[x];
edge[tot]=z;
head[x]=tot;
}
int findloop(int u,int in_edge) {
if(vis[u]) return u;
vis[u]=1;
for(int i=head[u]; i; i=nxt[i]) {
int v=ver[i];
if((in_edge^1)==i) continue;
int suf=findloop(v,i);
if(suf) {
c[++m]=u; vis[u]=2;
dl[m]=edge[i];
return suf==u?0:suf;
}
}
return 0;
}
int r,idx;
void getdis(int u,int f) {
is[u]=1;
for(int i=head[u]; i; i=nxt[i]) {
int v=ver[i];
if(v==f||vis[v]==2) continue;
dis[v]=dis[u]+edge[i];
if(dis[v]>dis[idx]||idx==0) idx=v;
getdis(v,u);
}
}
LL calc() {
LL ans=0;
for(int i=1; i<=m; i++) {
vis[c[i]]=1;
idx=0,getdis(c[i],c[i]);
f[i]=f[i+m]=dis[idx];
int rt=idx;
dis[rt]=0;
idx=0,getdis(rt,rt);
ans=max(ans,dis[idx]);
vis[c[i]]=2;
}
for(int i=1; i<=2*m; i++) {
if(i>m) dl[i]=dl[i-m];
s[i]=s[i-1]+dl[i];
}
deque<int> q;
for(int i=1; i<=2*m; i++) {
while(q.size()&&i-q.front()>=m) q.pop_front();
if(q.size()) ans=max(ans,f[i]+s[i]+f[q.front()]-s[q.front()]);
while(q.size()&&f[q.back()]-s[q.back()]<=f[i]-s[i]) q.pop_back();
q.push_back(i);
}
return ans;
}
int main() {
cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1; i<=n; i++) {
cin>>y>>z;
addedge(i,y,z); addedge(y,i,z);
}
for(int i=1; i<=n; i++) {
if(!is[i]) {
m=0;
findloop(i,0);
ret+=calc();
}
}
cout<<ret<<endl;
return 0;
}
P8819 [CSP-S 2022] 星战
发现可以反攻是原图是内向基环树森林。
所有点出度为 \(1\)。
我们发现出度是难以维护的,容易维护的是入度。
考虑每个点给一个随机权值 \(w_i\)。
每个点要维护的是 \(f_i\),表示以 \(i\) 为终点的所有点 \(w\) 和。
所有点出度为 \(1\),那么边的起点包含了 \(1\sim n\).
即 \(\sum w =\sum f\)
code
#include<bits/stdc++.h>
using namespace std;
typedef unsigned int unt;
const int N=5e5+10;
int n,m,q;
unt val[N],w[N],s[N],sum,ans;
vector<int> e[N];
mt19937 rnd(time(0));
int main() {
scanf("%d%d",&n,&m);
for(int i=1; i<=n; i++) val[i]=rnd(),ans+=val[i];
for(int i=1,u,v; i<=m; i++) {
scanf("%d%d",&u,&v);
w[v]+=val[u];
sum+=val[u];
}
for(int i=1; i<=n; i++) s[i]=w[i];
scanf("%d",&q);
for(int t,u,v; q; q--) {
scanf("%d",&t);
if(t==1) {
scanf("%d%d",&u,&v);
sum-=val[u];
w[v]-=val[u];
} else if(t==2) {
scanf("%d",&u);
sum-=w[u];
w[u]=0;
} else if(t==3) {
scanf("%d%d",&u,&v);
sum+=val[u];
w[v]+=val[u];
} else {
scanf("%d",&u);
sum+=s[u]-w[u];
w[u]=s[u];
}
if(sum==ans) puts("YES");
else puts("NO");
}
return 0;
}


