关于莫队
1.普通莫队
引入
先介绍莫队。
莫队是一种离线的算法。
莫队基于以下流程。
现在已知区间 \([l,r]\) 的贡献。
我们也可以推出 \([l,r-1]\),\([l-1,r]\),\([l+1,r]\),\([l,r+1]\) 区间的贡献。
诸如这样,我们挪动区间,顺便更新答案,就可以从上一次询问,更改到这一次询问。
比如我们要用莫队求这样一道题。
假设有 \(m\) 个询问,每次询问一个区间的和。
我们要用上次询问的贡献,更新这次的答案。
我们要合理的安排询问的顺序,使得 \(l\),\(r\) 指针移动距离尽量小。
若有 \(n=5\) 个数
比如这样询问 \([1,2],[4,5],[1,2],[3,4]\)
我们显然要更改它们顺序。
分块。
把询问左端点分块。把询问离线然后排序。
优先按左端点所在块排,左端点所在块相同就按右端点排。
此时,每个询问都在其左端点所在的块里。
然后我们发现,在同一块内,右端点是递增的,而左端点只会在块内跳。
像这样。 把 \((l,r)\) 抽象成二维坐标系里的点。
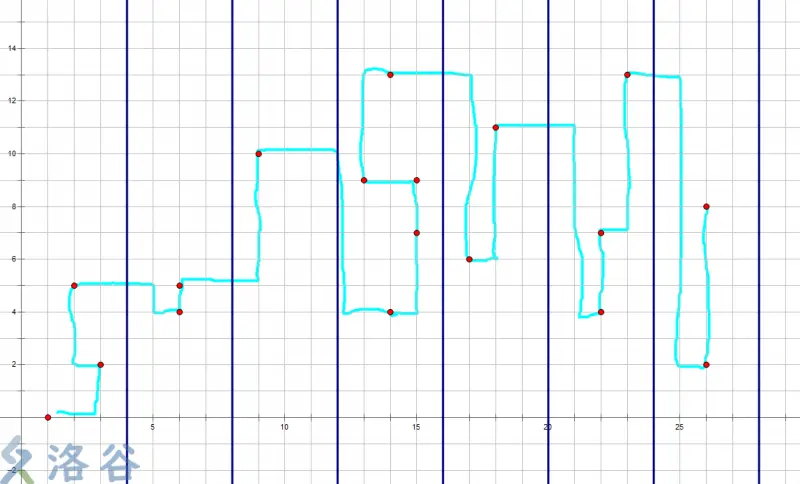
我们发现,这样来看指针移动距离是较小的。
有多少呢,设块大小为 \(s\) .
我们看对于每个询问,左指针移动 \(s\) 次;
对于每个块,右指针移动 \(n\) 次,有 \(\frac{n}{s}\) 个块。
所以共移动 \(qs+\dfrac{n^2}{s}\ge n\sqrt q\) 次。
当 \(s=\dfrac{n}{\sqrt q}\) 是最小。
当然了,也可以取 \(\sqrt n\).
这样我们就有了一个 \(O(n\sqrt q)\) 算法。
要注意,修改必须要 \(O(1)\) ,否则会变成更高复杂度。
应用
Luogu P2709
求区间内所有数出现次数的平方之和。
考虑莫队。
考虑每个数开一个桶 \(cnt\) 记录个数。
若添加元素,\(ans=ans+2*cnt+1,cnt=cnt+1\)
若删除元素,\(cnt=cnt-1,ans=ans-2*cnt-1\)
code
#include<bits/stdc++.h>
using namespace std;
const int N=50010;
struct qry {
int l,r,id;
} q[N];
int n,m,k,blk,a[N],cnt[N];
long long ans,res[N];
bool cmp(qry x,qry y) {
return (x.r/blk)==(y.r/blk)?x.l<y.l:x.r<y.r;
}
void add(int x) {
ans-=1ll*cnt[a[x]]*cnt[a[x]];
cnt[a[x]]++;
ans+=1ll*cnt[a[x]]*cnt[a[x]];
}
void del(int x) {
ans-=1ll*cnt[a[x]]*cnt[a[x]];
cnt[a[x]]--;
ans+=1ll*cnt[a[x]]*cnt[a[x]];
}
int main() {
scanf("%d%d%d",&n,&m,&k);
blk=sqrt(n);
for(int i=1; i<=n; i++) scanf("%d",&a[i]);
for(int i=1; i<=m; i++) {
scanf("%d%d",&q[i].l,&q[i].r);
q[i].id=i;
}
sort(q+1,q+1+m,cmp);
for(int i=1,l=1,r=0; i<=m; i++) {
int ql=q[i].l,qr=q[i].r;
while(l<ql) {del(l++);}
while(l>ql) {add(--l);}
while(r<qr) {add(++r);}
while(r>qr) {del(r--);}
res[q[i].id]=ans;
}
for(int i=1; i<=m; i++) printf("%lld\n",res[i]);
return 0;
}
Luogu P5268 [SNOI2017]一个简单的询问
每次询问求 \(\sum_x get(l1,r1,x) \cdot get(l2,r2,x)\)
\(get(l,r,x)\) 表示区间 \([l,r]\), \(x\) 出现次数。
看似这题有四个指针,不能用普通莫队做。
但是我们观察问题,发现 \(get(l,r,x)\) 可以拆成 \(get(1,r,x)-get(1,l-1,x)\).
于是我们可以拆问题,运用差分。
拆成形如这样的四个问题: \(get(1,r1,x)\cdot get(1,r2,x)\).
就可以只有两个指针了。
code
#include<bits/stdc++.h>
using namespace std;
const int N=5e4+10;
using LL=long long;
int n,a[N],q,m,blk;
int cnt1[N],cnt2[N];
LL ret[N],ans;
struct qry {
int l,r,p,op;
} b[N*4];
bool cmp(qry a,qry b) {
return a.r/blk==b.r/blk?a.l<b.l:a.r<b.r;
}
int main() {
scanf("%d",&n);
for(int i=1; i<=n; i++) scanf("%d",&a[i]);
scanf("%d",&q);
for(int i=1,l1,l2,r1,r2; i<=q; i++) {
scanf("%d%d%d%d",&l1,&r1,&l2,&r2);
b[++m]=qry{l1-1,l2-1,i,1};
b[++m]=qry{l1-1,r2,i,-1};
b[++m]=qry{r1,l2-1,i,-1};
b[++m]=qry{r1,r2,i,1};
}
blk=sqrt(n);
sort(b+1,b+1+m,cmp);
for(int i=1,l=0,r=0; i<=m; i++) {
int ql=b[i].l,qr=b[i].r;
while(l<ql) {
l++;
ans-=cnt1[a[l]]*cnt2[a[l]];
cnt1[a[l]]++;
ans+=cnt1[a[l]]*cnt2[a[l]];
}
while(l>ql) {
ans-=cnt1[a[l]]*cnt2[a[l]];
cnt1[a[l]]--;
ans+=cnt1[a[l]]*cnt2[a[l]];
l--;
}
while(r<qr) {
r++;
ans-=cnt1[a[r]]*cnt2[a[r]];
cnt2[a[r]]++;
ans+=cnt1[a[r]]*cnt2[a[r]];
}
while(r>qr) {
ans-=cnt1[a[r]]*cnt2[a[r]];
cnt2[a[r]]--;
ans+=cnt1[a[r]]*cnt2[a[r]];
r--;
}
ret[b[i].p]+=b[i].op*ans;
}
for(int i=1; i<=q; i++) printf("%lld\n",ret[i]);
return 0;
}
注意事项/技巧
奇偶性排序。
对于编号为奇数的块,右端点从小到大。
对于编号为偶数的块,右端点从大到小。
这样一个块处理完,右指针到 \(n\) 时,
就可以继续处理下个块,而不用回到开始。
大概时间减少 30%.
四个循环位置讨论(摘自 oi-wiki)
如果某时刻出现 \(l>r+1\) 的情况,那么会存在一个元素,它的加入次数是负数。
这在某些题目会出现问题,
例如我们如果用一个 set 维护区间中的所有数,就会出现「需要删除 set 中不存在的元素」的问题。
那么我们要避免 \(l>r+1\),因此有且仅有以下顺序是对的:
l--,r--,r++,l++ 正确
l--,r++,l++,r-- 正确
l--,r++,r--,l++ 正确
2.回滚莫队
引入
回滚莫队一般用于解决删除难,而增加易;或删除易,增加难的题目。
若只加不减,那么先排序。对于每个块,重置左右指针到块的末尾。
由于询问右端点有序,所以我们先将右指针移动到询问处。
此时记录答案。
然后将左端点移动到询问处。记录答案。
然后将答案还原,并且将左端点的操作复原。
这样我们就规避了删除操作。
这里有一个注意事项,当询问左右端点都在块内时,直接暴力求解。
若只减不加,那么此时在左端点所在块相同时,右端点从大到小。
对于每个块,重置左指针到块的开头,右指针到 \(n\) 处。
时间复杂度不变,但是常数大概大一点。
应用
AT joisc2014 c 歴史の研究
这题是不删除莫队,因为要维护最值。
然后做完了。
code
#include<bits/stdc++.h>
using namespace std;
using LL=long long;
const int N=1e5+10;
int n,m,a[N],c[N],b[N],blk,bl[N],cnt[N];
LL ans,ret[N];
struct Mo {int l,r,id; } q[N];
bool cmp(Mo x,Mo y) {return bl[x.l]==bl[y.l]?x.r<y.r:x.l<y.l;}
LL bf(int l,int r) {
LL res=0;
for(int i=l; i<=r; i++) cnt[c[i]]++;
for(int i=l; i<=r; i++) res=max(res,1ll*cnt[c[i]]*a[i]);
for(int i=l; i<=r; i++) cnt[c[i]]--;
return res;
}
int main() {
scanf("%d%d",&n,&m);
blk=sqrt(n);
for(int i=1; i<=n; i++) bl[i]=i/blk;
for(int i=1; i<=n; i++) scanf("%d",&a[i]),b[i]=a[i];
sort(b+1,b+1+n);
int len=unique(b+1,b+1+n)-b-1;
for(int i=1; i<=n; i++) c[i]=lower_bound(b+1,b+1+len,a[i])-b;
for(int i=1; i<=m; i++) {
scanf("%d%d",&q[i].l,&q[i].r);
q[i].id=i;
}
sort(q+1,q+1+m,cmp);
int l=1,r=0,l_;
for(int B=0,i=1; B<=bl[n]; B++) {
ans=0;
memset(cnt,0,sizeof(cnt));
l_=l=blk*(B+1),r=blk*(B+1)-1;
for(; bl[q[i].l]==B; i++) {
int ql=q[i].l,qr=q[i].r;
if(bl[ql]==bl[qr]) {
ret[q[i].id]=bf(ql,qr);
continue;
}
while(r<qr) {
++r; cnt[c[r]]++;
ans=max(ans,1ll*cnt[c[r]]*a[r]);
}
LL o=ans;
while(l>ql) {
--l; cnt[c[l]]++;
ans=max(ans,1ll*cnt[c[l]]*a[l]);
}
ret[q[i].id]=ans;
for(; l<l_; l++) cnt[c[l]]--;
ans=o;
}
}
for(int i=1; i<=m; i++) printf("%lld\n",ret[i]);
return 0;
}
Luogu P4137 mex
求区间最小没有出现的自然数。
不增加莫队。
每次删除,如果删除的数小于当前最小值,且删除后 \(cnt=0\), 那么就更新答案。
code
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;
int n,a[N],blk,m,bl[N],ret[N],cnt[N];
struct Mo {
int l,r,id;
} q[N];
bool cmp(Mo x,Mo y) {
return bl[x.l]==bl[y.l]?x.r>y.r:x.l<y.l;
}
int main() {
scanf("%d%d",&n,&m);
blk=sqrt(n);
for(int i=1; i<=n; i++) scanf("%d",&a[i]);
for(int i=1; i<=n; i++) bl[i]=i/blk;
for(int i=1; i<=m; i++) {
scanf("%d%d",&q[i].l,&q[i].r);
q[i].id=i;
}
sort(q+1,q+1+m,cmp);
for(int B=0,i=1; B<=bl[n]; B++) {
int l=B*blk,r=n,ans=N;
int l_=l;
memset(cnt,0,sizeof cnt);
for(int j=l; j<=r; j++) cnt[a[j]]++;
for(int i=0; i<N; i++) if(!cnt[i]) {ans=i; break;}
for(; bl[q[i].l]==B&&i<=m; i++) {
int ql=q[i].l,qr=q[i].r;
while(r>qr) {
cnt[a[r]]--;
if(cnt[a[r]]==0&&a[r]<ans)
ans=a[r];
r--;
}
int o=ans;
while(l<ql) {
cnt[a[l]]--;
if(cnt[a[l]]==0&&a[l]<ans)
ans=a[l];
l++;
}
ret[q[i].id]=ans;
ans=o;
while(l>l_) {
l--;
cnt[a[l]]++;
}
}
}
for(int i=1; i<=m; i++) printf("%d\n",ret[i]);
return 0;
}
3.带修莫队
引入
这里修改指单点修改。
莫队带修改,无非是增加一维时间维。
\([l,r,t]\)
\(\to [l-1,r,t]\)
\(\to [l+1,r,t]\)
\(\to [l,r-1,t]\)
\(\to [l,r+1,t]\)
\(\to [l,r,t-1]\)
\(\to [l,r,t+1]\)
优先按左端点所在块排,相同就按右端点所在块排,再相同就按时间排。
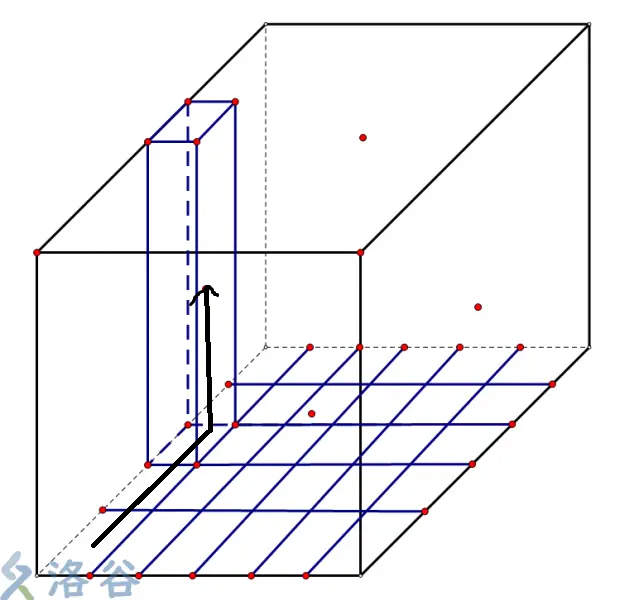
这时块长应做出调整了,设其为 \(s\).
每次询问,左右端点移动 \(s\).
每个右端点块,时间移动 \(n\),有 \(\dfrac{n^2}{s^2}\) 个块。
每个左端点块,右端点移动 \(n\),可不计。
\(qs+\dfrac{n^3}{s^2}\ge \sqrt[3]{q^2}n\).
\(s=\dfrac{n}{\sqrt[3]{q}}\) 最小。
时间复杂度 \(O(q^{\dfrac{2}{3}}n)\),在 \(O(n^{\dfrac{5}{3}})\) 量级。
还是比暴力快。
应用
Luogu P1903
板子。
code
#include<bits/stdc++.h>
using namespace std;
const int N=133355,M=1e6+10;
int sum,cnt[M],a[N],ret[N],cntq,cntr,n,m,blk;
struct Mo {
int l,r,t,id;
} qq[N],qr[N];
void addx(int x) {sum+=!cnt[x]; cnt[x]++;}
void delx(int x) {cnt[x]--; sum-=!cnt[x];}
void updx(int x,int t) {
if(qq[x].l<=qr[t].l&&qr[t].l<=qq[x].r) {
delx(a[qr[t].l]);
addx(qr[t].r);
}
swap(a[qr[t].l],qr[t].r);
}
bool cmp(Mo a,Mo b) {
return a.l/blk==b.l/blk?a.r/blk==b.r/blk?a.t<b.t:a.r<b.r:a.l<b.l;
}
int main() {
scanf("%d%d",&n,&m); blk= ceil(exp((log(n)+log(m))/3));
for(int i=1; i<=n; i++) scanf("%d",&a[i]);
for(int i=1; i<=m; i++) {
char op[5]; int l,r;
scanf("%s%d%d",op,&l,&r);
if(op[0]=='Q') {
++cntq;
qq[cntq]=(Mo){l,r,cntr,cntq};
} else {
++cntr;
qr[cntr]=(Mo){l,r,0,0};
}
}
sort(qq+1,qq+cntq+1,cmp);
int lcur=1,rcur=0,tcur=0;
for(int i=1; i<=cntq; i++) {
while(lcur>qq[i].l) addx(a[--lcur]);
while(lcur<qq[i].l) delx(a[lcur++]);
while(rcur>qq[i].r) delx(a[rcur--]);
while(rcur<qq[i].r) addx(a[++rcur]);
while(tcur<qq[i].t) updx(i,++tcur);
while(tcur>qq[i].t) updx(i,tcur--);
ret[qq[i].id]=sum;
}
for(int i=1; i<=cntq; i++) printf("%d\n",ret[i]);
return 0;
}
4.树上莫队
引入
我们把树转换成欧拉序即可。
我们要把第一次访问节点的时间和回溯的时间记录下来。
记第一次访问节点为 \(fir_u\),回溯为 \(lst_u\).
若要处理子树 \(u\),那么区间则是 \(fir_u \sim lst_u\).
若要处理链 \(u \sim v\),钦定 \(fir_u<fir_v\).
分类讨论,若 \(u\) 为 \(lca\),即没有转折。
区间为 \(fir_u \sim fir_v\).
若 \(u\) 不为 \(lca\) 。
区间为 \(lst_u \sim fir_u\),还要加上 \(lca\),因为 \(lca\) 并不包括在这个区间里。
注意:若有一个节点出现了两次,说明这个节点没有贡献,要减掉。
应用
Luogu P4074 [WC2013] 糖果公园
带修的树上的莫队。
处理链。
code
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10,logn=20;
const int blk=3420;
int n,b,m,v[N],w[N],a[N];
int f[N][logn],dep[N];
int num,seq[N],fir[N],lst[N];
int cntq,cntr;
int c[N],cnt[N];
long long ans,ret[N];
vector<int> e[N];
struct Mo {
int l,r,t,lc,id;
} qq[N],qr[N];
bool cmp(Mo x,Mo y) {
return x.l/blk==y.l/blk?x.r/blk==y.r/blk?x.t<y.t:x.r<y.r:x.l<y.l;
}
void dfs(int u,int father) {
dep[u]=dep[father]+1;
f[u][0]=father;
for(int i=1; i<logn; i++) f[u][i]=f[f[u][i-1]][i-1];
fir[u]=++num; seq[num]=u;
for(int i=0; i<(int)e[u].size(); i++) {
int v=e[u][i];
if(v==father) continue;
dfs(v,u);
}
lst[u]=++num; seq[num]=u;
}
int Lca(int x,int y) {
if(dep[x]>dep[y]) swap(x,y);
for(int i=logn-1; i>=0; i--) {
if(dep[f[y][i]]>=dep[x]) y=f[y][i];
}
if(x==y) return x;
for(int i=logn-1; i>=0; i--) {
if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
}
return f[x][0];
}
void add(int p) {
c[p]^=1;
if(c[p]) {
cnt[a[p]]++;
ans+=1ll*w[cnt[a[p]]]*v[a[p]];
} else {
ans-=1ll*w[cnt[a[p]]]*v[a[p]];
cnt[a[p]]--;
}
}
void upd(int i,int t) {
int cl=fir[qr[t].l],cr=lst[qr[t].l];
if(qq[i].l<=cl&&cl<=qq[i].r) add(qr[t].l);
if(qq[i].l<=cr&&cr<=qq[i].r) add(qr[t].l);
swap(qr[t].r,a[qr[t].l]);
if(qq[i].l<=cl&&cl<=qq[i].r) add(qr[t].l);
if(qq[i].l<=cr&&cr<=qq[i].r) add(qr[t].l);
}
void solve() {
sort(qq+1,qq+1+cntq,cmp);
int l=1,r=0,t=0;
for(int i=1; i<=cntq; i++) {
int ql=qq[i].l,qr=qq[i].r,qt=qq[i].t;
while(l>ql) add(seq[--l]);
while(r<qr) add(seq[++r]);
while(l<ql) add(seq[l++]);
while(r>qr) add(seq[r--]);
while(t<qt) upd(i,++t);
while(t>qt) upd(i,t--);
if(qq[i].lc) add(qq[i].lc);
ret[qq[i].id]=ans;
if(qq[i].lc) add(qq[i].lc);
}
}
int main() {
scanf("%d%d%d",&n,&b,&m);
for(int i=1; i<=b; i++) scanf("%d",&v[i]);
for(int i=1; i<=n; i++) scanf("%d",&w[i]);
for(int i=1,u,v; i<n; i++) {
scanf("%d%d",&u,&v);
e[u].push_back(v);
e[v].push_back(u);
}
for(int i=1; i<=n; i++) scanf("%d",&a[i]);
dfs(1,1);
for(int i=1,op,x,y; i<=m; i++) {
scanf("%d%d%d",&op,&x,&y);
if(op==0) {
cntr++;
qr[cntr]={x,y,0,0,0};
} else {
cntq++;
if(fir[x]>fir[y]) swap(x,y);
int lc=Lca(x,y);
if(lc==x) {
qq[cntq]={fir[x],fir[y],cntr,0,cntq};
} else qq[cntq]={lst[x],fir[y],cntr,lc,cntq};
}
}
solve();
for(int i=1; i<=cntq; i++) printf("%lld\n",ret[i]);
return 0;
}
CF375D
处理子树。
code
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;
int n,m,blk,a[N],seq[N],num,fir[N],lst[N],ret[N],cnt[N],dcnt[N];
vector<int> e[N];
struct Mo {
int l,r,k,id;
} q[N];
bool cmp(Mo x,Mo y) {
return x.l/blk==y.l/blk?x.r<y.r:x.l<y.l;
}
void dfs(int u,int father) {
seq[++num]=u;
fir[u]=num;
for(int i=0; i<(int)e[u].size(); i++) {
int v=e[u][i];
if(v==father) continue;
dfs(v,u);
}
lst[u]=num;
}
void add(int p) {
int u=seq[p];
cnt[a[u]]++;
dcnt[cnt[a[u]]]++;
}
void del(int p) {
int u=seq[p];
dcnt[cnt[a[u]]]--;
cnt[a[u]]--;
}
int main() {
scanf("%d%d",&n,&m); blk=sqrt(n);
for(int i=1; i<=n; i++) scanf("%d",&a[i]);
for(int u,v,i=1; i<n; i++) {
scanf("%d%d",&u,&v);
e[u].push_back(v); e[v].push_back(u);
}
dfs(1,0);
for(int u,k,i=1; i<=m; i++) {
scanf("%d%d",&u,&k);
q[i].l=fir[u]; q[i].r=lst[u];
q[i].id=i; q[i].k=k;
}
sort(q+1,q+1+m,cmp);
int l=1,r=0;
for(int i=1; i<=m; i++) {
int ql=q[i].l,qr=q[i].r;
while(l>ql) add(--l);
while(r<qr) add(++r);
while(l<ql) del(l++);
while(r>qr) del(r--);
ret[q[i].id]=dcnt[q[i].k];
}
for(int i=1; i<=m; i++) printf("%d\n",ret[i]);
return 0;
}
5.二次离线莫队
引入
可以通过二次离线来降低复杂度。
应用
Luogu P5047 [Ynoi2019 模拟赛] Yuno loves sqrt technology II
求区间逆序对数。 卡空间。
首先显然有一个 \(O(n\sqrt n \log n)\) 的暴力。
注意到,我们在指针移动时所需的询问形如:在区间 \([l,r]\) 内有多少个数 \(\leq k\),
而这可以差分为在前缀 \([1,r]\) 内有多少个数 \(\leq k\)。
我们可以使用可持久化分块。但是空间大,被卡。
我们还可以将这 \(O(n\sqrt n)\) 个询问记录下来同一处理。但这样空间还是被卡。
我们进一步观察,设 \((r,x)\) 为前缀 \([1,r]\) 中 \(\le x\) 的个数。
当 \(l\) 向左移动到 \(l'\)
贡献为 \(\sum_{i \in [l',l)} (r,a_i-1)-(i,a_i-1)\)
向右同理。
当 \(r\) 向右移动到 \(r'\)
此处省略。
观察贡献形式,都形如这样。
\(\sum_{i}\space (x,a_i)\).
或这样。
\(\sum_{i}\space {i,a_i}\).
可以用扫描线。
code
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n,q;
struct DS1 {
int t[N];
void add(int p) {
while(p<=n) {t[p]++; p+=p&-p;}
}
int qry(int p){
int ret=0;
while(p) {ret+=t[p]; p^=p&-p;}
return ret;
}
} T;
struct DS2 {
int ob[505],o[N],BS;
void add(int p) {
int bp=p/BS+1,br=bp*BS;
for(int i=bp; i<=BS; i++) ob[i]++;
for(int i=p; i<br; i++) o[i]++;
}
int qry(int p) {return ob[p/BS]+o[p];}
} T2;
int a[N],x[N];
long long ans[N];
struct Data2 {int l,r,c,d,p; };
vector<Data2> s[N];
struct Data {int l,r,p; } b[N];
long long s1[N],s2[N];
int BS;
bool cmp(Data A,Data B){
return A.l/BS==B.l/BS?((A.l/BS)&1)^(A.r<B.r):A.l<B.l;
}
void MoQ() {
sort(b+1,b+1+q,cmp);
int l=1,r=0;
for(int i=1; i<=q; i++) {
if(b[i].l<l) {
ans[b[i].p]-=s1[l-1]-s1[b[i].l-1];
s[r].push_back((Data2){b[i].l,l-1,1,-1,b[i].p});
l=b[i].l;
}
if(r<b[i].r) {
ans[b[i].p]+=1ll*(r+b[i].r+1-2*l)*(b[i].r-r)/2-(s2[b[i].r]-s2[r]);
s[l-1].push_back((Data2){r+1,b[i].r,1,0,b[i].p});
r=b[i].r;
}
if(l<b[i].l) {
ans[b[i].p]+=s1[b[i].l-1]-s1[l-1];
s[r].push_back((Data2){l,b[i].l-1,-1,-1,b[i].p});
l=b[i].l;
}
if(b[i].r<r) {
ans[b[i].p]-=1ll*(r+b[i].r+1-2*l)*(r-b[i].r)/2-(s2[r]-s2[b[i].r]);
s[l-1].push_back((Data2){b[i].r+1,r,-1,0,b[i].p});
r=b[i].r;
}
}
}
int main() {
scanf("%d%d",&n,&q);
for(int i=1; i<=n; i++) {
scanf("%d",&a[i]);
x[i]=a[i];
}
sort(x+1,x+n+1);
for(int i=1; i<=n; i++) a[i]=lower_bound(x+1,x+n+1,a[i])-x;
for(int i=1; i<=n; i++) {
s2[i]=s2[i-1]+T.qry(a[i]);
T.add(a[i]);
s1[i]=s1[i-1]+T.qry(a[i]-1);
}
for(int i=1; i<=q; i++) {
scanf("%d%d",&b[i].l,&b[i].r);
b[i].p=i;
}
BS=1.0*n/sqrt(q)+5;
MoQ();
T2.BS=sqrt(n)+1;
for(int i=1; i<=n; i++) {
T2.add(a[i]);
for(int k=0; k<(int)s[i].size(); k++) {
Data2 u=s[i][k];
for(int j=u.l; j<=u.r; j++)
ans[u.p]+=u.c*T2.qry(a[j]+u.d);
}
}
for(int i=1; i<=q; i++) ans[b[i].p]+=ans[b[i-1].p];
for(int i=1; i<=q; i++) printf("%lld\n",ans[i]);
return 0;
} //部分摘自 @command_block 的博客
6.???经验之谈
可以使用莫队的情况
允许离线的,区间询问的,单点修改的,
数颜色,计算个数,关于下标的,有关权值的……
各种奇怪的……
可以用莫队。
P6072 『MdOI R1』Path
考虑枚举分割点,即一条路径在某个子树内,另一条在子树外,形成两个区间,就变成了若干询问。
这些询问可以用莫队处理,加上字典树即可。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号