线段树高难度操作
1.李超树
引入
李超线段树是一种维护直线、线段的数据结构。
可插入一条线段或直线,并查询 \(x=p\) 的点上最值的 \(y\) .
构建
李超线段树用了标记永久化的思想。
李超树的每一个节点,设区间为 \([L,R]\)
保存最优直线的编号,这个编号是指 \([L,R]\) 之间 \(mid=\frac{L+R}{2}\),这个点上的最值的编号。
同时这个编号也可以表示在所有 \([L,R]\) 内的点最值可能的编号。
以维护直线最大值为例:
我们如何更新呢?
1.若当前区间没有标记,我们就打上标记。
2.若新直线完全高于旧直线,就替代。
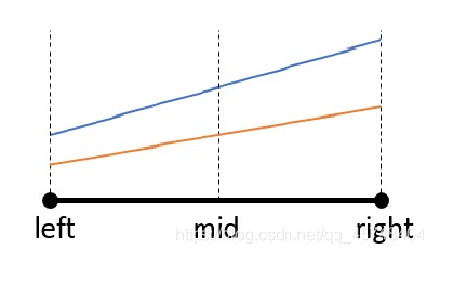
3.若新直线完全低于旧直线,就放弃。
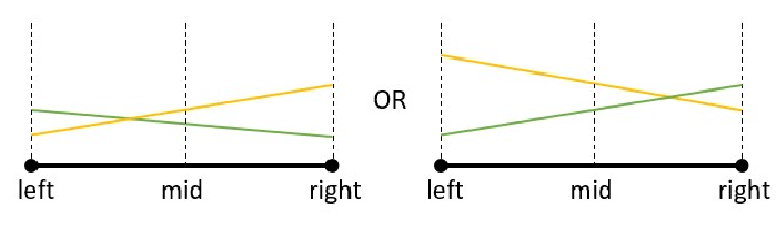
4.若有交点,如下图:
我们递归更新。
对于查询操作,我们从线段树根节点开始递归,找到所有包括 \(x=p\) 的区间 ( \(\log n\) 个).
取当 \(x=p\) 最大值即可。
因为所有包括 \(x=p\) 的区间保存的最优直线都是有可能对其贡献的。
讲不清楚,看代码实现。
code
void modify(int p,int l,int r,int t) {
if(l==r) {
if(g(t,l)>g(tree[p],l)) tree[p]=t;
return ;
}
int mid=(l+r)/2;
if(g(t,mid)>g(tree[p],mid)) swap(t,tree[p]);
if(g(t,l)>g(tree[p],l)) modify(p*2,l,mid,t);
else if(g(t,r)>g(tree[p],r)) modify(p*2+1,mid+1,r,t);
}
LL query(int p,int l,int r,int pos) {
if(l==r) return g(tree[p],pos);
int mid=(l+r)/2;
LL res=-inf;
if(pos<=mid) res=query(p*2,l,mid,pos);
else res=query(p*2+1,mid+1,r,pos);
return max(res,g(tree[p],pos));
}
Luogu P4655
优化 DP.
\(dp_i=min(dp_j+a_j*h_x+b_j)\).
即查询在 \(x=h_x\) 上直线最值。
code
#include<bits/stdc++.h>
using namespace std;
using LL=long long;
const LL inf=2e18;
const int N=1e5+10,M=1e6+10;
LL a[N],b[N],h[N],w[N],f[N];
int n,tree[M*4];
LL g(int t,int x) {return a[t]*x+b[t];}
void modify(int p,int l,int r,int t) {
if(l==r) {
if(g(t,l)<g(tree[p],l)) tree[p]=t;
return ;
}
int mid=(l+r)/2;
if(g(t,mid)<g(tree[p],mid)) swap(t,tree[p]);
if(g(t,l)<g(tree[p],l)) modify(p*2,l,mid,t);
else if(g(t,r)<g(tree[p],r)) modify(p*2+1,mid+1,r,t);
}
LL query(int p,int l,int r,int pos) {
if(l==r) return g(tree[p],pos);
int mid=(l+r)/2;
LL res=inf;
if(pos<=mid) res=query(p*2,l,mid,pos);
else res=query(p*2+1,mid+1,r,pos);
return min(res,g(tree[p],pos));
}
int main() {
scanf("%d",&n); b[0]=inf;
for(int i=1; i<=n; i++) scanf("%lld",&h[i]);
for(int i=1; i<=n; i++) scanf("%lld",&w[i]),w[i]+=w[i-1];
a[1]=-2*h[1]; b[1]=h[1]*h[1]-w[1];
modify(1,0,M,1);
for(int i=2; i<=n; i++) {
f[i]=h[i]*h[i]+w[i-1]+query(1,0,M,h[i]);
a[i]=-2*h[i]; b[i]=f[i]+h[i]*h[i]-w[i];
modify(1,0,M,i);
}
printf("%lld\n",f[n]);
return 0;
}
2.线段树合并
引入
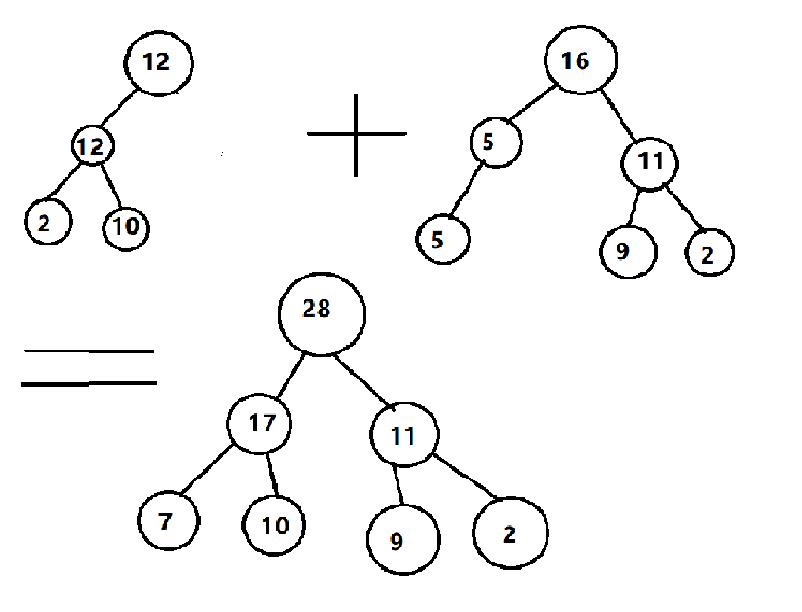
两颗线段树值域相同的,他们可以合并。
从根节点开始,递归实现。
如果递归到一个节点两颗中有一颗没有值,那么就直接替代上,然后返回。
或者接着更新。直到更新到叶子节点后直接合并。
应用
P4556 雨天的尾巴
每个树的节点维护一颗值域线段树。
空间复杂度 \(O(n\log n)\).
时间复杂度 \(O(n\log n)\).
code
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
const int N=1e5+10;
int tot,head[N],ver[2*N],nxt[2*N];
int lc[60*N],rc[60*N],d[60*N],t[60*N];
int top[N],fa[N],deep[N],son[N],sum[N],qx[N],qy[N],qz[N],ans[N];
int n,m,rt[N],cnt,R,num;
void addedge(int x,int y) {
ver[++tot]=y;
nxt[tot]=head[x];
head[x]=tot;
}
void dfs1(int u) {
sum[u]=1; int maxx=-1;
for(int i=head[u]; i; i=nxt[i]) {
int v=ver[i];
if(!deep[v]) {
deep[v]=deep[u]+1; fa[v]=u;
dfs1(v); sum[u]+=sum[v];
if(sum[v]>maxx) {maxx=sum[v]; son[u]=v;}
}
}
}
void dfs2(int u,int topf) {
top[u]=topf;
if(!son[u]) return ;
dfs2(son[u],topf);
for(int i=head[u]; i; i=nxt[i]) {
int v=ver[i];
if(!top[v]) dfs2(v,v);
}
}
int lca(int u,int v) {
while(top[u]!=top[v]) {
if(deep[top[u]]<deep[top[v]]) swap(u,v);
u=fa[top[u]];
}
if(deep[u]<deep[v]) return u;
else return v;
}
void pushup(int p) {
if(d[lc[p]]>=d[rc[p]]) {
d[p]=d[lc[p]]; t[p]=t[lc[p]];
} else {
d[p]=d[rc[p]]; t[p]=t[rc[p]];
}
}
int modify(int p,int x,int y,int pos,int val) {
if(!p) p=++cnt;
if(x==y) {d[p]+=val; t[p]=x; return p;}
int mid=(x+y)/2;
if(pos<=mid) lc[p]=modify(lc[p],x,mid,pos,val);
else rc[p]=modify(rc[p],mid+1,y,pos,val);
pushup(p);
return p;
}
int merge(int p,int q,int x,int y) {
if(!p) return q;
if(!q) return p;
if(x==y) {d[p]+=d[q]; t[p]=x; return p;}
int mid=(x+y)/2;
lc[p]=merge(lc[p],lc[q],x,mid);
rc[p]=merge(rc[p],rc[q],mid+1,y);
pushup(p); return p;
}
void Redfs(int u) {
for(int i=head[u]; i; i=nxt[i]) {
int v=ver[i];
if(deep[v]>deep[u]) {
Redfs(v);
rt[u]=merge(rt[u],rt[v],1,R);
}
}
if(d[rt[u]]) ans[u]=t[rt[u]];
}
int main() {
scanf("%d%d",&n,&m);
for(int i=1,x,y; i<n; i++) {
scanf("%d%d",&x,&y);
addedge(y,x); addedge(x,y);
}
deep[1]=1; dfs1(1); dfs2(1,1);
for(int i=1; i<=m; i++) {
scanf("%d%d%d",&qx[i],&qy[i],&qz[i]);
R=max(R,qz[i]);
}
for(int i=1; i<=m; i++) {
int s=lca(qx[i],qy[i]);
rt[qx[i]]=modify(rt[qx[i]],1,R,qz[i],1);
rt[qy[i]]=modify(rt[qy[i]],1,R,qz[i],1);
rt[s]=modify(rt[s],1,R,qz[i],-1);
if(fa[s]) rt[fa[s]]=modify(rt[fa[s]],1,R,qz[i],-1);
}
Redfs(1);
for(int i=1; i<=n; i++) printf("%d\n",ans[i]);
return 0;
}
CF208E
询问每个节点子树深度为 \(k\) 有几个节点。
先把询问离线挂在节点上。
每个节点建立一个以深度为值域的线段树。
保存子树内节点的深度。
然后合并即可。
code
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10,M=4e6+10,logn=19;
int n,m,f[N][logn],depth[N],fa[N];
int ans[N];
int rt[N],dat[M],tot,ls[M],rs[M];
vector<int> e[N];
vector<pair<int,int> > qy[N];
void dfs(int u,int father) {
f[u][0]=father; depth[u]=depth[father]+1;
for(int i=1; i<logn; i++) f[u][i]=f[f[u][i-1]][i-1];
for(int i=0; i<(int)e[u].size(); i++) {
int v=e[u][i];
if(v==father) continue;
dfs(v,u);
}
}
int LCA(int u,int k) {
int v=u;
for(int i=logn-1; i>=0; i--) {
if(depth[u]-depth[f[v][i]]<=k)
v=f[v][i];
}
return v;
}
int modify(int p,int l,int r,int pos,int val) {
if(!p) p=++tot;
if(l==r) {dat[p]+=val; return p;}
int mid=(l+r)>>1;
if(pos<=mid) ls[p]=modify(ls[p],l,mid,pos,val);
else rs[p]=modify(rs[p],mid+1,r,pos,val);
dat[p]=dat[ls[p]]+dat[rs[p]];
return p;
}
int merge(int p1,int p2,int l,int r) {
if(!p1) return p2;
if(!p2) return p1;
if(l==r) {
dat[p1]+=dat[p2]; return p1;
}
int mid=(l+r)>>1;
ls[p1]=merge(ls[p1],ls[p2],l,mid);
rs[p1]=merge(rs[p1],rs[p2],mid+1,r);
dat[p1]=dat[ls[p1]]+dat[rs[p1]];
return p1;
}
int query(int p,int l,int r,int x) {
if(!p) return 0;
if(l==r) return dat[p];
int mid=(l+r)>>1;
if(x<=mid) return query(ls[p],l,mid,x);
else return query(rs[p],mid+1,r,x);
}
void solve(int u,int father) {
for(int i=0; i<(int)e[u].size(); i++) {
int v=e[u][i];
if(v==father) continue;
solve(v,u);
rt[u]=merge(rt[u],rt[v],1,2*n);
}
for(int i=0; i<(int)qy[u].size(); i++) {
int k=qy[u][i].first,id=qy[u][i].second;
ans[id]=query(rt[u],1,2*n,depth[u]+k)-1;
}
}
int main() {
scanf("%d",&n);
for(int i=1; i<=n; i++) {
scanf("%d",&fa[i]);
if(fa[i]!=0)
e[fa[i]].push_back(i);
}
for(int i=1; i<=n; i++) {
if(!fa[i]) dfs(i,0);
}
scanf("%d",&m);
for(int i=1,u,k; i<=m; i++) {
scanf("%d%d",&u,&k);
int F=LCA(u,k);
if(F==0) ans[i]=0;
else
qy[F].push_back(make_pair(k,i));
}
for(int i=1; i<=n; i++) rt[i]=modify(rt[i],1,2*n,depth[i],1);
for(int i=1; i<=n; i++) {
if(!fa[i]) solve(i,0);
}
for(int i=1; i<=m; i++) printf("%d ",ans[i]);
return 0;
}
Luogu P3224 永无乡
题意:加边,维护每个联通块权值第 \(k\) 大。
以点权值的建立线段树。
用并查集合并,同时线段树也合并。
code
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10,M=32e5+10;
int n,m,q,rt[N],dat[M][2],tot,val[N],fa[N],ls[M],rs[M];
int getf(int x) {
if(x==fa[x]) return x;
else return fa[x]=getf(fa[x]);
}
void pushup(int p) {
dat[p][0]=dat[ls[p]][0]+dat[rs[p]][0];
}
int modify(int p,int l,int r,int pos,int id) {
if(!p) p=++tot;
if(l==r) {dat[p][0]++; dat[p][1]=id; return p;}
int mid=(l+r)/2;
if(pos<=mid) ls[p]=modify(ls[p],l,mid,pos,id);
else rs[p]=modify(rs[p],mid+1,r,pos,id);
pushup(p);
return p;
}
int merge(int p1,int p2,int l,int r) {
if(!p1) return p2;
if(!p2) return p1;
if(l==r) {
dat[p1][0]+=dat[p2][0];
return p1;
}
int mid=(l+r)/2;
ls[p1]=merge(ls[p1],ls[p2],l,mid);
rs[p1]=merge(rs[p1],rs[p2],mid+1,r);
pushup(p1);
return p1;
}
int query(int p,int l,int r,int k) {
if(dat[p][0]<k||p==0) return -1;
if(l==r) return dat[p][1];
int mid=(l+r)/2;
if(dat[ls[p]][0]>=k) return query(ls[p],l,mid,k);
else return query(rs[p],mid+1,r,k-dat[ls[p]][0]);
}
int main() {
scanf("%d%d",&n,&m);
for(int i=1; i<=n; i++) fa[i]=i;
for(int i=1; i<=n; i++) {
scanf("%d",&val[i]);
rt[i]=modify(rt[i],1,n,val[i],i);
}
for(int i=1,u,v; i<=m; i++) {
scanf("%d%d",&u,&v);
int fu=getf(u),fv=getf(v);
if(fv==fu) continue;
fa[fv]=fu;
rt[fu]=merge(rt[fu],rt[fv],1,n);
}
scanf("%d",&q);
for(int e1,e2; q; q--) {
char s[3];
scanf("%s",s);
scanf("%d%d",&e1,&e2);
if(s[0]=='B') {
int fu=getf(e1),fv=getf(e2);
if(fv==fu) continue;
fa[fv]=fu;
rt[fu]=merge(rt[fu],rt[fv],1,n);
} else {
int fu=getf(e1);
printf("%d\n",query(rt[fu],1,n,e2));
}
}
return 0;
}
Luogu P3899 [湖南集训] 更为厉害
...
code
#include<bits/stdc++.h>
using namespace std;
using LL=long long;
const int N=3e5+10;
const int M=7e6+10;
int n,q,rt[N],tot,ls[M],rs[M];
int siz[N],depth[N];
LL dat[M],ans[N];
vector<int> e[N];
vector<pair<int,int> > qy[N];
void pushup(int p) {
dat[p]=dat[ls[p]]+dat[rs[p]];
}
int modify(int p,int l,int r,int x,int k) {
if(!p) p=++tot;
if(l==r) {
dat[p]=dat[p]+k; return p;
}
int mid=(l+r)/2;
if(x<=mid) ls[p]=modify(ls[p],l,mid,x,k);
else rs[p]=modify(rs[p],mid+1,r,x,k);
pushup(p); return p;
}
int merge(int p1,int p2,int l,int r) {
if(!p1) return p2;
if(!p2) return p1;
if(l==r) {
dat[p1]+=dat[p2];
return p1;
}
int mid=(l+r)/2;
ls[p1]=merge(ls[p1],ls[p2],l,mid);
rs[p1]=merge(rs[p1],rs[p2],mid+1,r);
pushup(p1); return p1;
}
LL query(int p,int l,int r,int x,int y) {
if(!p) return 0;
if(x<=l&&r<=y) return dat[p];
int mid=(l+r)>>1;
LL res=0;
if(x<=mid) res+=query(ls[p],l,mid,x,y);
if(y>mid) res+=query(rs[p],mid+1,r,x,y);
return res;
}
void dfs(int u,int father) {
siz[u]=1; depth[u]=depth[father]+1;
for(int i=0; i<(int)e[u].size(); i++) {
int v=e[u][i];
if(v==father) continue;
dfs(v,u);
siz[u]+=siz[v];
rt[u]=merge(rt[u],rt[v],1,n);
}
rt[u]=modify(rt[u],1,n,depth[u],siz[u]-1);
for(int i=0; i<(int)qy[u].size(); i++) {
int k=qy[u][i].first,id=qy[u][i].second;
ans[id]=ans[id]+1ll*min(k,depth[u]-1)*(siz[u]-1);
ans[id]=ans[id]+query(rt[u],1,n,depth[u]+1,depth[u]+k);
}
}
int main() {
scanf("%d%d",&n,&q);
for(int i=1,u,v; i<n; i++) {
scanf("%d%d",&u,&v);
e[u].push_back(v); e[v].push_back(u);
}
for(int i=1,p,k; i<=q; i++) {
scanf("%d%d",&p,&k);
qy[p].push_back(make_pair(k,i));
}
dfs(1,1);
for(int i=1; i<=q; i++) printf("%lld\n",ans[i]);
return 0;
}
Luogu P1600 天天爱跑步
每个人在树上 \(u-v\) 路径,每秒移动一个点。
询问每个节点 \(u\) 在 \(w_u\) 时间上恰好几个人经过。
考虑向上的路径 \(u-lca\),设观察员 \(x\).
满足 \(depth_u-depth_x = w_x\) ,观察员就答案加一。
移项,\(depth_u = w_x+depth_x\).
注意:只有在路径 \(u-lca\) 上的点才能计算答案。
所以要树上差分。
即在 \(u\) 上存一个 \(depth_u\),然后合并上去,在 \(lca\) 把 \(depth\) 减掉。
然后在 \(x\) 上查询等于 \(w_x+depth_x\) 有多少个。
向下的路径 \(lca-v\)
满足 \(depth_u+depth_x-2*depth_lca = w_x\) ,观察员就答案加一。
移项 \(depth_u-2*depth_lca = w_x-depth_x\).
同理了。
code
#include<bits/stdc++.h>
using namespace std;
const int N=3e5+10,M=12e6+10,logn=19;
int n,m,w[N];
struct Tree {
int dat[M],ls[M],rs[M],tot,rt[N];
} tr[2];
int f[N][logn],depth[N];
int ans[N];
vector<int> e[N];
void dfs(int u,int father) {
f[u][0]=father; depth[u]=depth[father]+1;
for(int i=1; i<logn; i++) f[u][i]=f[f[u][i-1]][i-1];
for(int i=0; i<(int)e[u].size(); i++) {
int v=e[u][i];
if(v==father) continue;
dfs(v,u);
}
}
int LCA(int u,int v) {
if(depth[v]>depth[u]) swap(u,v);
for(int i=logn-1; i>=0; i--) {
if(depth[f[u][i]]>=depth[v]) u=f[u][i];
}
if(u==v) return u;
for(int i=logn-1; i>=0; i--) {
if(f[u][i]!=f[v][i]) u=f[u][i],v=f[v][i];
}
return f[u][0];
}
int modify(int id,int p,int l,int r,int pos,int val) {
if(!p) p=++tr[id].tot;
if(l==r) {tr[id].dat[p]+=val; return p;}
int mid=(l+r)>>1;
if(pos<=mid) tr[id].ls[p]=modify(id,tr[id].ls[p],l,mid,pos,val);
else tr[id].rs[p]=modify(id,tr[id].rs[p],mid+1,r,pos,val);
return p;
}
int merge(int id,int p1,int p2,int l,int r) {
if(!p1) return p2;
if(!p2) return p1;
if(l==r) {
tr[id].dat[p1]+=tr[id].dat[p2];
return p1;
}
int mid=(l+r)>>1;
tr[id].ls[p1]=merge(id,tr[id].ls[p1],tr[id].ls[p2],l,mid);
tr[id].rs[p1]=merge(id,tr[id].rs[p1],tr[id].rs[p2],mid+1,r);
return p1;
}
int query(int id,int p,int l,int r,int k) {
if(!p) return 0;
if(l==r) return tr[id].dat[p];
int mid=(l+r)>>1;
if(k<=mid) return query(id,tr[id].ls[p],l,mid,k);
else return query(id,tr[id].rs[p],mid+1,r,k);
}
void solve(int u,int father) {
for(int i=0; i<(int)e[u].size(); i++) {
int v=e[u][i];
if(v==father) continue;
solve(v,u);
tr[0].rt[u]=merge(0,tr[0].rt[u],tr[0].rt[v],0,2*n);
tr[1].rt[u]=merge(1,tr[1].rt[u],tr[1].rt[v],-n,n);
}
ans[u]+=query(0,tr[0].rt[u],0,2*n,w[u]+depth[u]);
ans[u]+=query(1,tr[1].rt[u],-n,n,w[u]-depth[u]);
}
int main() {
scanf("%d%d",&n,&m);
for(int i=1,u,v; i<n; i++) {
scanf("%d%d",&u,&v);
e[u].push_back(v); e[v].push_back(u);
}
for(int i=1; i<=n; i++) scanf("%d",&w[i]);
dfs(1,0);
for(int i=1,u,v; i<=m; i++) {
scanf("%d%d",&u,&v);
int lca=LCA(u,v);
tr[0].rt[u]=modify(0,tr[0].rt[u],0,2*n,depth[u],1);
tr[0].rt[f[lca][0]]=modify(0,tr[0].rt[f[lca][0]],0,2*n,depth[u],-1);
tr[1].rt[v]=modify(1,tr[1].rt[v],-n,n,depth[u]-2*depth[lca],1);
tr[1].rt[lca]=modify(1,tr[1].rt[lca],-n,n,depth[u]-2*depth[lca],-1);
}
solve(1,0);
for(int i=1; i<=n; i++) printf("%d ",ans[i]);
return 0;
}
CF932F
李超线段树合并。
code
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e5+5,T=2e5,Bs=1e5,inf=1e18;
int n,A[N],B[N],rt[N],cnt;
int k[N],b[N],f[N],tot;
int g(int t,int x) {
x-=Bs;
return k[t]*x+b[t];
}
vector<int>e[N];
int tr[N<<5],ls[N<<5],rs[N<<5];
void update(int &u,int l,int r,int x) {
if(!u) {
u=++cnt;
tr[u]=x;
return ;
}
if(g(x,l)<g(tr[u],l)&&g(x,r)<g(tr[u],r)) {
tr[u]=x;
return ;
}
if(g(x,l)>=g(tr[u],l)&&g(x,r)>=g(tr[u],r)) {
return ;
}
int mid=(l+r)>>1;
if(k[x]>k[tr[u]]) {
if(g(x,mid)>g(tr[u],mid)) update(ls[u],l,mid,x);
else update(rs[u],mid+1,r,tr[u]),tr[u]=x;
}
else {
if(g(x,mid)>g(tr[u],mid)) update(rs[u],mid+1,r,x);
else update(ls[u],l,mid,tr[u]),tr[u]=x;
}
}
int query(int u,int l,int r,int x) {
if(!u) return inf;
if(l==r) return g(tr[u],x);
int mid=(l+r)>>1;
if(x<=mid) return min(g(tr[u],x),query(ls[u],l,mid,x));
else return min(g(tr[u],x),query(rs[u],mid+1,r,x));
}
int merge(int u,int v,int l,int r) {
if(!u||!v) return u|v;
if(l==r) {
if(g(tr[u],l)>g(tr[v],l)) tr[u]=tr[v];
return u;
}
int mid=(l+r)>>1;
ls[u]=merge(ls[u],ls[v],l,mid);
rs[u]=merge(rs[u],rs[v],mid+1,r);
update(u,l,r,tr[v]);
return u;
}
void dfs(int u,int fa) {
for(int i=0,len=e[u].size(); i<len; i++) {
int v=e[u][i];
if(v==fa) continue;
dfs(v,u);
rt[u]=merge(rt[u],rt[v],0,T);
}
if(rt[u]) {
f[u]=query(rt[u],0,T,A[u]+Bs);
}
++tot;
b[tot]=f[u];
k[tot]=B[u];
update(rt[u],0,T,tot);
}
signed main() {
scanf("%lld",&n);
for(int i=1; i<=n; i++) scanf("%lld",&A[i]);
for(int i=1; i<=n; i++) scanf("%lld",&B[i]);
for(int i=1; i<n; i++) {
int x,y;
scanf("%lld %lld",&x,&y);
e[x].push_back(y);
e[y].push_back(x);
}
dfs(1,0);
for(int i=1; i<=n; i++)
printf("%lld ",f[i]);
return 0;
}
一些经验
线段树合并的题,通常在树上。
计算一些有关子树或路径上的统计问题。
可能和 dsu on tree 有点相似.
3.主席树
引入
主席树是可持久化线段树。
可以加入数并维护版本。
具体怎么操作呢?
因为每次加入一个数只会改变 \(\log n\) 个线段树上的点。
所以其他的点是可以不变的。
其他的点可以继承上个版本的。
所以我们递归下去,若左儿子被修改,那么右子树不变,同理。
应用
Luogu P3834
查询静态区间第 \(k\) 小。
每个下标开一个线段树,然后将线段树做一个“前缀和”。
由于多次查询,所以不能用线段树合并。
那么我们就用主席树。
主席树建好之后,比如查询 \([l,r]\),那我们用版本 \(r\) 减去版本 \(l-1\),在线段树上二分。
注意这里不用每个节点都减出来,只用在查询路上减就行了。
code
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;
const int M=5e6+10;
int n,q,m;
int a[N],b[N];
int rt[N],ls[M],rs[M],dat[M],tot;
int build(int p,int l,int r) {
p=++tot;
if(l==r) return p;
int mid=(l+r)>>1;
ls[p]=build(ls[p],l,mid);
rs[p]=build(rs[p],mid+1,r);
return p;
}
int modify(int pre,int l,int r,int pos) {
int p=++tot;
ls[p]=ls[pre]; rs[p]=rs[pre]; dat[p]=dat[pre]+1;
if(l==r) return p;
int mid=(l+r)>>1;
if(pos<=mid) ls[p]=modify(ls[pre],l,mid,pos);
else rs[p]=modify(rs[pre],mid+1,r,pos);
return p;
}
int query(int p1,int p2,int l,int r,int k) {
if(l==r) return l;
int mid=(l+r)>>1;
int x=dat[ls[p2]]-dat[ls[p1]];
if(x>=k) return query(ls[p1],ls[p2],l,mid,k);
else return query(rs[p1],rs[p2],mid+1,r,k-x);
}
int main() {
scanf("%d%d",&n,&q);
for(int i=1; i<=n; i++) {
scanf("%d",&a[i]);
b[i]=a[i];
}
sort(b+1,b+1+n);
m=unique(b+1,b+1+n)-b-1;
rt[0]=build(1,1,m);
for(int i=1; i<=n; i++) {
int t=lower_bound(b+1,b+1+m,a[i])-b;
rt[i]=modify(rt[i-1],1,m,t);
}
for(int i=1,x,y,z; i<=q; i++) {
scanf("%d%d%d",&x,&y,&z);
int t=query(rt[x-1],rt[y],1,m,z);
printf("%d\n",b[t]);
}
return 0;
}
Luogu 2633
查询树上路径第 \(k\) 大。
每个节点线段树保存根节点到它的路径的权值。
可以用主席树。
设查询 \(u,v\).
那么计算 \(u+v-lca-fa_{lca}\) 中第 \(k\) 大、
code
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10,M=23e5+10,logn=20;
int n,m,q,a[N],b[N];
int rt[N],tot,ls[M],rs[M],dat[M];
int f[N][logn],depth[N];
vector<int> e[N];
int build(int l,int r) {
int p=++tot;
if(l>=r) return p;
int mid=(l+r)>>1;
ls[p]=build(l,mid);
rs[p]=build(mid+1,r);
return p;
}
int modify(int pre,int l,int r,int pos) {
int p=++tot;
ls[p]=ls[pre]; rs[p]=rs[pre]; dat[p]=dat[pre]+1;
if(l==r) return p;
int mid=(l+r)>>1;
if(pos<=mid) ls[p]=modify(ls[pre],l,mid,pos);
else rs[p]=modify(rs[pre],mid+1,r,pos);
return p;
}
void dfs(int u,int father) {
f[u][0]=father; depth[u]=depth[father]+1;
for(int i=1; i<logn; i++) f[u][i]=f[f[u][i-1]][i-1];
rt[u]=modify(rt[father],1,m,a[u]);
for(int i=0; i<(int)e[u].size(); i++) {
int v=e[u][i];
if(v==father) continue;
dfs(v,u);
}
}
int LCA(int u,int v) {
if(depth[v]>depth[u]) swap(u,v);
for(int i=logn-1; i>=0; i--) {
if(depth[f[u][i]]>=depth[v]) u=f[u][i];
}
if(u==v) return u;
for(int i=logn-1; i>=0; i--) {
if(f[u][i]!=f[v][i]) u=f[u][i],v=f[v][i];
}
return f[u][0];
}
int query(int p1,int p2,int p3,int p4,int l,int r,int k) {
if(l==r) return l;
int mid=(l+r)>>1;
int x=dat[ls[p1]]+dat[ls[p2]]-dat[ls[p3]]-dat[ls[p4]];
if(x>=k) return query(ls[p1],ls[p2],ls[p3],ls[p4],l,mid,k);
else return query(rs[p1],rs[p2],rs[p3],rs[p4],mid+1,r,k-x);
}
int main() {
scanf("%d%d",&n,&q);
for(int i=1; i<=n; i++) {
scanf("%d",&a[i]);
b[i]=a[i];
}
sort(b+1,b+1+n);
m=unique(b+1,b+1+n)-b-1;
rt[0]=build(1,m);
for(int i=1; i<=n; i++) {
a[i]=lower_bound(b+1,b+1+m,a[i])-b;
}
for(int i=1,u,v; i<n; i++) {
scanf("%d%d",&u,&v);
e[u].push_back(v);
e[v].push_back(u);
}
dfs(1,0);
int lastans=0;
for(int i=1,u,v,w; i<=q; i++) {
scanf("%d%d%d",&u,&v,&w);
u=u^lastans;
int F=LCA(u,v);
int G=f[F][0];
int t=query(rt[u],rt[v],rt[F],rt[G],1,m,w);
printf("%d\n",lastans=b[t]);
}
return 0;
}
Luogu 4755
计算多少个数对 \((i,j)\) ,满足 \(a_i\cdot a_j \le max(a[i,j])\).
这题我写的是笛卡尔树上线段树合并。
当然也可以用主席树。
分治,先把当前区间最大值取出来,然后用一下主席树计算。
然后最大值左边和最大值右边继续分治。
code
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10,M=32e5+10,inf=1e9+10;
int n,a[N],L[N],R[N],stk[N],tp;
int ls[M],rs[M],dat[M],rt[N],tot;
long long ans;
void pushup(int p) {
dat[p]=dat[ls[p]]+dat[rs[p]];
}
int modify(int p,int l,int r,int pos) {
if(!p) p=++tot;
if(l==r) {dat[p]++; return p;}
int mid=(l+r)>>1;
if(pos<=mid) ls[p]=modify(ls[p],l,mid,pos);
else rs[p]=modify(rs[p],mid+1,r,pos);
pushup(p);
return p;
}
int kth(int p,int l,int r,int k) {
if(l==r) return l;
int mid=(l+r)>>1;
if(dat[ls[p]]>=k) return kth(ls[p],l,mid,k);
else return kth(rs[p],mid+1,r,k-dat[ls[p]]);
}
int query(int p,int l,int r,int x,int y) {
if(x>y) return 0;
if(!p) return 0;
if(x<=l&&r<=y) return dat[p];
int mid=(l+r)>>1,res=0;
if(x<=mid) res+=query(ls[p],l,mid,x,y);
if(y>mid) res+=query(rs[p],mid+1,r,x,y);
return res;
}
int merge(int p1,int p2,int l,int r) {
if(!p1) return p2;
if(!p2) return p1;
if(l==r) {
dat[p1]+=dat[p2];
return p1;
}
int mid=(l+r)/2;
ls[p1]=merge(ls[p1],ls[p2],l,mid);
rs[p1]=merge(rs[p1],rs[p2],mid+1,r);
pushup(p1);
return p1;
}
int solve(int p1,int p2,int val) {
if(dat[p1]>dat[p2]) swap(p1,p2);
for(int i=1; i<=dat[p1]; i++) {
int x=kth(p1,1,inf,i);
ans=ans+query(p2,1,inf,1,val/x);
}
p1=merge(p1,p2,1,inf);
return p1;
}
void dfs(int u) {
if(L[u]) {
dfs(L[u]);
rt[u]=solve(rt[L[u]],rt[u],a[u]);
}
if(R[u]) {
dfs(R[u]);
rt[u]=solve(rt[R[u]],rt[u],a[u]);
}
}
int main() {
scanf("%d",&n);
for(int i=1; i<=n; i++) scanf("%d",&a[i]);
for(int i=1; i<=n; i++) {
while(tp&&a[stk[tp]]<a[i]) L[i]=stk[tp--];
R[stk[tp]]=i;
stk[++tp]=i;
}
for(int i=1; i<=n; i++) rt[i]=modify(rt[i],1,inf,a[i]);
dfs(stk[1]);
for(int i=1; i<=n; i++) if(a[i]==1) ans++;
printf("%lld\n",ans);
return 0;
}
Luogu P4602 [CTSC2018] 混合果汁
有 \(n\) 种果汁,有美味度,价格和购买上限。
任意购买果汁然后混合,美味度为这些果汁美味度最小值。
计算价格不超过 \(g\),果汁体积大于 \(lim\),美味度最大值。
最小值最大,显然二分美味度。
以美味度为下标建立一颗主席树。
然后线段树上二分即可。
code
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=100005;
struct juice{
int d, p, l;
}jc[N];
int n, m;
bool cmp(juice a, juice b) {
return a.d<b.d;
}
ll tr[N<<5], mon[N<<5];
int ls[N<<5], rs[N<<5], cnt, st[N], rt[N];
void update(int &u, int pre, int l, int r, int pos, ll val) {
u=++cnt;
tr[u]=tr[pre]+val; ls[u]=ls[pre]; rs[u]=rs[pre];
if(l==r) {
mon[u]=tr[u]*l;
return ;
}
int mid=l+r>>1;
if(pos<=mid) update(ls[u], ls[pre], l, mid, pos, val);
if(pos>mid) update(rs[u], rs[pre], mid+1, r, pos, val);
mon[u]=mon[ls[u]]+mon[rs[u]];
}
ll query(int u, int v, int l, int r, ll k) {
if(l==r) {
if(k>tr[u]-tr[v]) return 1e18+5;
return k*l;
}
ll lsm=tr[ls[u]]-tr[ls[v]];
int mid=l+r>>1;
if(lsm>=k) return query(ls[u], ls[v], l, mid, k);
else return mon[ls[u]]-mon[ls[v]]+query(rs[u], rs[v], mid+1, r, k-lsm);
}
int main() {
scanf("%d %d", &n, &m);
for(int i=1; i<=n; i++) {
scanf("%d %d %d", &jc[i].d, &jc[i].p, &jc[i].l);
st[i]=jc[i].d;
}
sort(st+1, st+1+n);
sort(jc+1, jc+1+n, cmp);
for(int i=1; i<=n; i++) {
update(rt[i], rt[i-1], 1, N, jc[i].p, jc[i].l);
}
for(ll i=1, g, L; i<=m; i++) {
scanf("%lld %lld", &g, &L);
int l=-1, r=N;
while(l+1<r) {
int mid=l+r>>1;
int mr=lower_bound(st+1, st+1+n, mid)-st-1;
if(query(rt[n], rt[mr], 1, N, L)<=g)l=mid;
else r=mid;
}
printf("%d\n", l);
}
return 0;
}
4.线段树分治
引入
可以解决一些有撤销的题。
把元素存在的时间存下来,然后区间修改到线段树上 \(\log n\) 个节点。
在线段树上的这些节点的 \(vector\) 上加入这个元素。
如果一个节点 代表 \([l,r]\) 区间,那么这个节点里的元素都是在 \([l,r]\) 里全部存在的。
所以儿子的信息可以继承父亲的。
但是儿子计算完之后,要把信息还原。
那么 DFS 整颗线段树即可。
这样,我们就规避了撤销的操作。
应用
Luogu P5227 [AHOI2013]连通图
问删边之后图是否联通。
先把边时间存一下,然后区间修改。
DFS 到一个节点,先把节点上的边全部用并查集加上。
并查集维护 \(siz\) 代表当前集合的大小。
若 \(siz=n\) 那么就联通。
那么我们如何把信息还原呢?
我们开个栈记录并查集的操作即可。
这里用按秩合并。
code
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10,M=2e5+10;
int n,m,q,last[M],e[M][2],f[N],siz[N];
vector<int> dat[N<<2];
struct del {
int u,v,s;
del() {}
del(int u_,int v_,int s_) {u=u_; v=v_; s=s_;}
};
stack<del> s;
void ins(int p,int l,int r,int x,int y,int id) {
if(x>y) return ;
if(x<=l&&r<=y) {
dat[p].push_back(id);
return ;
}
int mid=(l+r)/2;
if(x<=mid) ins(p*2,l,mid,x,y,id);
if(y>mid) ins(p*2+1,mid+1,r,x,y,id);
}
int get(int x) {
while(x!=f[x]) x=f[x];
return x;
}
void merge(int u,int v) {
if(siz[u]>siz[v]) swap(u,v);
s.push(del(u,v,siz[u]));
f[u]=v; siz[v]+=siz[u]; siz[u]=0;
}
void dfs(int p,int l,int r,bool flag) {
int o=s.size();
for(int i=0; i<(int)dat[p].size(); i++) {
int x=dat[p][i],u=get(e[x][0]),v=get(e[x][1]);
if(u==v) continue;
merge(u,v);
if(siz[u]==n||siz[v]==n) flag=1;
}
int mid=(l+r)>>1;
if(l==r) puts(flag?"Connected":"Disconnected");
else dfs(p*2,l,mid,flag),dfs(p*2+1,mid+1,r,flag);
while((int)s.size()>o) {
del sb=s.top();
f[sb.u]=sb.u; siz[sb.v]-=sb.s; siz[sb.u]=sb.s;
s.pop();
}
}
int main() {
scanf("%d%d",&n,&m);
for(int i=1; i<=m; i++) {
scanf("%d%d",&e[i][0],&e[i][1]);
}
scanf("%d",&q);
for(int i=1,b,x; i<=q; i++) {
scanf("%d",&b);
for(int j=1; j<=b; j++) {
scanf("%d",&x);
ins(1,1,q,last[x]+1,i-1,x);
last[x]=i;
}
}
for(int i=1; i<=m; i++) ins(1,1,q,last[i]+1,q,i);
for(int i=1; i<=n; i++) siz[i]=1,f[i]=i;
dfs(1,1,q,0);
return 0;
}
Luogu P5631 最小mex生成树
mex 为:最小的、没有出现在集合中的自然数。
现在你要求出一个这个图的生成树,使得其边权集合的 mex 尽可能小。
我们枚举 mex 的值,此时只有边权不是 \(mex\) 的边才能用。
我们检验是否联通即可。
每个边存在的时间为 \([0-w_j-1]\),\([w_j+1,10^5]\)
可撤销并查集。
code
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10,M=2e6+10,W=1e5+10;
int n,m,e[M][3],ans=W;
int fa[N],siz[N];
vector<int> dat[N<<2];
struct node {
int x,y,z;
node() {}
node(int x_,int y_,int z_) {x=x_; y=y_; z=z_;}
} ;
stack<node> st;
void ins(int p,int l,int r,int x,int y,int i) {
if(x>y) return ;
if(x<=l&&r<=y) {
dat[p].push_back(i);
return ;
}
int mid=(l+r)>>1;
if(x<=mid) ins(p*2,l,mid,x,y,i);
if(y>mid) ins(p*2+1,mid+1,r,x,y,i);
}
int get(int x) {
while(x!=fa[x]) x=fa[x];
return x;
}
void merge(int x,int y) {
if(siz[x]>siz[y]) swap(x,y);
fa[x]=y; siz[y]+=siz[x];
st.push(node(x,y,siz[x]));
}
void dfs(int p,int l,int r) {
int o=st.size();
for(int i=0; i<(int)dat[p].size(); i++) {
int x=dat[p][i],u=get(e[x][0]),v=get(e[x][1]);
if(u==v) continue;
merge(u,v);
}
if(l==r) {
if(siz[get(1)]==n)
ans=min(ans,l);
} else {
int mid=(l+r)>>1;
dfs(p*2,l,mid); dfs(p*2+1,mid+1,r);
}
while((int)st.size()>o) {
node D=st.top(); st.pop();
fa[D.x]=D.x; siz[D.y]-=D.z;
}
}
int main() {
scanf("%d%d",&n,&m);
for(int i=1; i<=m; i++) {
scanf("%d%d%d",&e[i][0],&e[i][1],&e[i][2]);
ins(1,1,W,1,e[i][2]-1,i); ins(1,1,W,e[i][2]+1,W,i);
}
for(int i=1; i<=n; i++) fa[i]=i,siz[i]=1;
dfs(1,1,W);
return printf("%d\n",ans),0;
}
CF1140F
若扩展一个集合,指的是存在 \((a,b),(a,y0),(x0,b) \in S\),将 \((x0,y0)\) 加入集合。
问集合支持删点,加点,扩展集合的大小。
将 \((a,b)\) 抽象为二分图两边的两个点。
那么若有 \(a,b\),\(a,y0\),\(x0,b\) 边,这四个点就联通。
此时就加入 \(x0,y0\) 边。
那么答案就是所有联通块左边点 \(\times\) 右边点。
线段树分治维护。
code
#include<bits/stdc++.h>
using namespace std;
using LL=long long;
const int N=3e5+5;
int q,top;
LL ans=0;
int fa[2*N],h[2*N],l[2*N],ht[2*N];
struct Node{
int x,y;
} d[N];
map<int,int> rf[N];
vector<Node> tr[N<<2];
struct Sk{
int x,y,add;
}sk[N];
void update(int u,int l,int r,int L,int R,Node e) {
if(L<=l&&r<=R) {
tr[u].push_back(e);;
return ;
}
int mid=(l+r)>>1;
if(L<=mid)update(u<<1,l,mid,L,R,e);
if(R>mid) update(u<<1|1,mid+1,r,L,R,e);
}
int find(int x) {
while(fa[x]!=x) x=fa[x];
return x;
}
void merge(int x,int y) {
int fx=find(x),fy=find(y);
if(fx==fy) return ;
ans+=1ll*h[fx]*l[fy]+1ll*l[fx]*h[fy];
if(ht[fx]>ht[fy]) swap(fx,fy);
sk[++top]=Sk{fx,fy,ht[fx]==ht[fy]};
if(ht[fx]==ht[fy]) ht[fy]++;
h[fy]+=h[fx];
l[fy]+=l[fx];
fa[fx]=fy;
}
void solve(int u,int L,int R) {
int o=top;
for(int i=0; i<(int)tr[u].size(); i++) {
merge(tr[u][i].x,tr[u][i].y+N);
}
if(L==R) {
printf("%lld ",ans);
} else {
int mid=(L+R)>>1;
solve(u<<1,L,mid);
solve(u<<1|1,mid+1,R);
}
while(top>o) {
ht[fa[sk[top].x]]-=sk[top].add;
fa[sk[top].x]=sk[top].x;
h[sk[top].y]-=h[sk[top].x];
l[sk[top].y]-=l[sk[top].x];
ans-=h[sk[top].x]*l[sk[top].y];
ans-=l[sk[top].x]*h[sk[top].y];
top--;
}
}
int main() {
scanf("%d",&q);
for(int i=1,x,y; i<=q; i++) {
scanf("%d%d",&x,&y);
d[i].x=x; d[i].y=y;
if(!rf[x][y]) rf[x][y]=i;
else {
update(1,1,q,rf[x][y],i-1,Node{x,y});
rf[x][y]=0;
}
}
for(int i=q; i>=1; i--) {
if(rf[d[i].x][d[i].y]) {
update(1,1,q,i,q,Node{d[i].x,d[i].y});
rf[d[i].x][d[i].y]=0;
}
}
for(int i=1; i<=N; i++) fa[i]=i,h[i]=1,ht[i]=1;
for(int i=N+1; i<=2*N; i++) fa[i]=i,l[i]=1,ht[i]=1;
ans=0;
solve(1,1,q);
return 0;
}
CF576E Painting Edges
尽管是判断合法后才会执行操作,但这并不影响我们线段树分治。
把每条边不同颜色存在的时间区间拿出来,例如在 \(t\) 时刻更改了颜色,把区间分为 \([1,t],[t+1,n]\)
那么我们在 \(t\) 的叶子节点判断,如果合法那么 \([t+1,n]\) 为新的颜色,否则为旧的。
我们先把区间挂上去,然后在区间前把这个区间的颜色判断出来。
5.猫树
关于处理最大子段和这种问题,我们可以建立一个线段树,
每个节点 \([l,r]\),对于 \(\forall i \in [l,r]\) ,维护 \([i,mid]\) 或 \([mid,i]\) 的信息。
对于查询 \([x,y]\),我们找到 \(x,y\) 在线段树上的 \(lca\),并用这个节点的信息去处理,所以是可以在线的。


