图的连通性算法
前置知识
时间戳(dfn):图的深度优先遍历中,节点第一次被访问的次序。
搜索树:由所有发生递归的边构成。
无向图的割点与桥
割点:若 \(u\) 是割点,那么删去 \(u\) 点及其相连的边,原图分成二或以上个连通块。
桥(割边):若 \(e\) 是桥,那么删去 \(e\) 边,原图分成二个连通块。
让我们引入一个新概念:追溯值 \(low\).
\(low_x\) 为已下节点时间戳最小值。
1.搜索树中 \(subtree(x)\) 中的点。
2.经过一条不在搜索树上的边,能够到达 \(subtree(x)\) 中的节点。
感性理解为不经过祖先节点可以达到的最前的节点。
割边判定法则:
存在搜索树上 \(x\) 儿子节点 \(y\),满足 \(dfn_x<low_y\).
性质:桥一定是搜索树上的节点,环上一定不存在桥。
感性理解,由于子树的点追溯不到更前的点,所以成为了“封闭”状态。
割点判定法则:
存在搜索树上 \(x\) 儿子节点 \(y\),满足 \(dfn_x\le low_y\).
特别地,若 \(x\) 是搜索树的根节点,
则 \(x\) 是割点仅当搜索树上存在至少两个节点满足上述条件。
无向图双联通分量
点双联通图:不存在割点的无向图。
边双联通图:不存在桥的无向图。
点双联通分量(vdcc):无向图的极大点双联通子图。
边双联通分量(edcc):无向图的极大边双联通子图。
上述极大的含义深刻:
若 \(G\) 极大,则不满足有 \(G'\) 也满足双联通,且 \(G \subseteq G'\).
若一个图是点双且节点数不小于3,则任意两点同时处于至少一个简单环中。
如一个图是边双,则任意一条边一定被包含至少一个简单环中。
edcc 的求法:
删除所有桥即可。
code
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+10,M=2e6+10;
int n,m,tot=1,head[N],ver[2*M],nxt[2*M],rt,num;
int c[N],dcc;
int dfn[N],low[N];
bool brg[2*M];
vector<int> DCC[N];
void addedge(int x,int y) {
ver[++tot]=y;
nxt[tot]=head[x];
head[x]=tot;
}
void tarjan(int u,int in_edge) {
low[u]=dfn[u]=++num;
for(int i=head[u]; i; i=nxt[i]) {
int v=ver[i];
if(!dfn[v]) {
tarjan(v,i);
low[u]=min(low[u],low[v]);
if(low[v]>dfn[u]) {
brg[i]=brg[i^1]=true;
}
} else if(i!=(in_edge^1)) {
low[u]=min(low[u],dfn[v]);
}
}
}
void dfs(int u) {
c[u]=dcc; DCC[dcc].push_back(u);
for(int i=head[u]; i; i=nxt[i]) {
int v=ver[i];
if(c[v]||brg[i]) continue;
dfs(v);
}
}
int main() {
scanf("%d%d",&n,&m);
for(int i=1,u,v; i<=m; i++) {
scanf("%d%d",&u,&v);
addedge(u,v); addedge(v,u);
}
for(int i=1; i<=n; i++)
if(!dfn[i]) {
rt=i; tarjan(i,0);
}
for(int i=1; i<=n; i++)
if(!c[i]) {
++dcc; dfs(i);
}
printf("%d\n",dcc);
for(int i=1; i<=dcc; i++) {
printf("%d ",DCC[i].size());
for(int j=0; j<DCC[i].size(); j++)
printf("%d ",DCC[i][j]);
puts("");
}
return 0;
}
edcc 的缩点:
将每个 edcc 看成一个节点,把桥边 \((x,y)\) 看成 \(x\) 所在的 edcc 与 \(y\) 所在的 edcc 连边。
vdcc 的求法:
有一个性质导致 vdcc 无法删除所有割点来求。
因为一个割点可能包括在很多个 vdcc 中。
具体求法:
维护一个栈,当第一次访问到一个节点,将节点入栈。
当割点判定条件成立时,无论 \(x\) 是否为根,弹出栈内所有节点,直到 \(y\) 被弹出。
刚弹出的所有节点与 \(x\) 一起构成一个 vdcc.
code
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+10,M=2e6+10;
int head[N],ver[2*M],nxt[2*M],tot=1;
int n,m,dfn[N],low[N],num,rt;
int dcc,cut[N];
int stk[N],tp;
vector<int> DCC[N];
void addedge(int x,int y) {
ver[++tot]=y;
nxt[tot]=head[x];
head[x]=tot;
}
void tarjan(int u,int in_edge) {
dfn[u]=low[u]=++num;
int flag=0;
if(u==rt&&head[u]==0) {
++dcc;
DCC[dcc].push_back(u);
return ;
}
stk[++tp]=u;
for(int i=head[u]; i; i=nxt[i]) {
int v=ver[i];
if(!dfn[v]) {
tarjan(v,i);
low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u]) {
flag++;
if(u!=rt||flag>1) cut[u]=1;
dcc++;
int z;
do {
z=stk[tp--];
DCC[dcc].push_back(z);
} while(z!=v);
DCC[dcc].push_back(u);
}
} else if(i!=(in_edge^1))
low[u]=min(low[u],dfn[v]);
}
}
int main() {
scanf("%d%d",&n,&m);
for(int i=1,u,v; i<=m; i++) {
scanf("%d%d",&u,&v);
if(u==v) continue;
addedge(u,v); addedge(v,u);
}
for(int i=1; i<=n; i++)
if(!dfn[i]) {
rt=i; tarjan(rt,0);
}
printf("%d\n",dcc);
for(int i=1; i<=dcc; i++) {
printf("%d ",DCC[i].size());
for(int j=0; j<DCC[i].size(); j++) {
printf("%d ",DCC[i][j]);
}
puts("");
}
return 0;
}
vdcc 的缩点:
设图中有 \(p\) 个割点,\(t\) 个 vdcc.
建立一张有 \(p+t\) 个节点的新图。
让每个割点和包含他的 vdcc 连边。
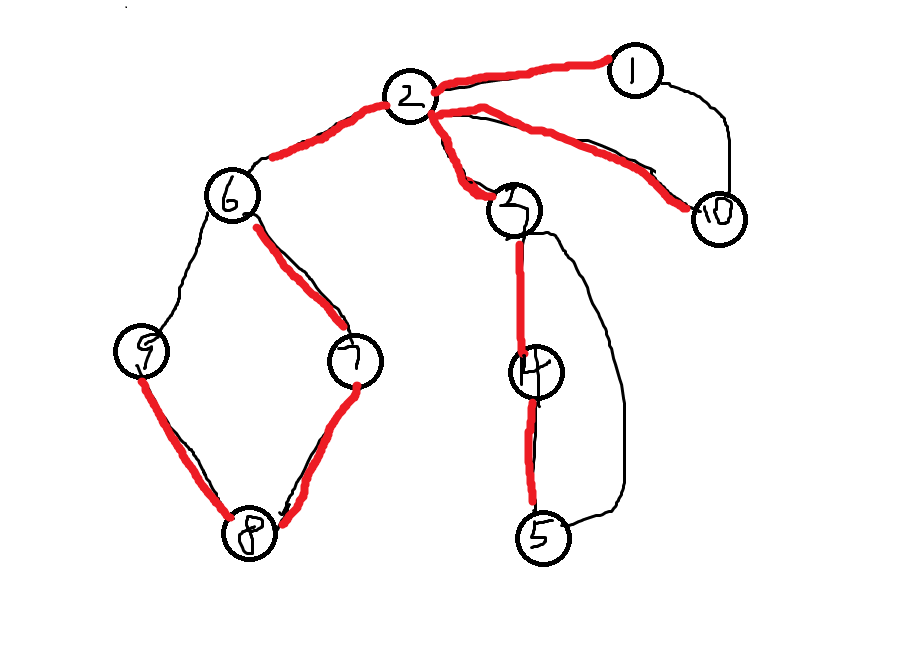
上述图中:(节点编号代表时间戳)。
(红色边代表搜索树边)
割点是 \(2,3,6\).
桥是:\((2,3),(2,6).\)
边双是:\(\{1,2,10\},\{3,4,5\},\{6,7,8,9\}\).
点双是:\(\{2,6\},\{1,2,10\},\{2,3\},\{6,7,8,9\},\{3,4,5\}\).
有向图的强联通分量
强联通图:任意两点都互相有路径到达。
强联通分量(scc):有向图的极大强联通子图。
让我们引入一个新概念:追溯值 \(low\).
\(low_x\) 为满足已下条件节点时间戳最小值。
1.该点在栈中。
2.存在一条从 \(subtree(x)\) 出发一条边,以该点为终点。
Tarjan 算法按照这样计算:
1.当 \(x\) 第一次被访问,\(x\) 入栈。初始化 \(low_x=dfn_x\).
2.扫描每条出边:若 \(y\) 没被访问,则递归,令 \(low_x=min(low_x,low_y)\).
若 \(y\) 被访问且在栈中,令 \(low_x=min(low_x,dfn_y)\).
3.当 \(x\) 回溯之前,判断是否 \(dfn_x=low_x\),若成立,则从栈中弹出节点直到 \(x\) 出栈、
此时弹出的所有节点构成一个强联通分量。
这里的栈可感性理解为还未被加入到强联通分量的剩下的点。
scc 的缩点:
同理。
code
#include<bits/stdc++.h>
using namespace std;
const int N=1e4+10,M=1e5+10;
int head[N],ver[2*M],nxt[2*M],tot;
int dfn[N],low[N];
int stk[N],ins[N],c[N];
vector<int> SCC[N];
int a[N],val[N],ans[N],mx;
int n,m,num,tp,scc;
int hc[N],vc[2*M],nc[2*M],tc,dr[N];
int que[N],hd,tl;
void addedge(int x,int y) {
ver[++tot]=y;
nxt[tot]=head[x];
head[x]=tot;
}
void tarjan(int u) {
dfn[u]=low[u]=++num;
stk[++tp]=u; ins[u]=1;
for(int i=head[u]; i; i=nxt[i]) {
int v=ver[i];
if(!dfn[v]) {
tarjan(v);
low[u]=min(low[u],low[v]);
} else if(ins[v])
low[u]=min(low[u],dfn[v]);
}
if(low[u]==dfn[u]) {
scc++; int v;
do {
v=stk[tp--]; ins[v]=0;
c[v]=scc; SCC[scc].push_back(v);
val[scc]+=a[v];
} while(u!=v);
}
}
void add_c(int x,int y) {
vc[++tc]=y;
nc[tc]=hc[x];
hc[x]=tc;
}
int main() {
scanf("%d%d",&n,&m);
for(int i=1; i<=n; i++) scanf("%d",&a[i]);
for(int i=1,u,v; i<=m; i++) {
scanf("%d%d",&u,&v);
addedge(u,v);
}
for(int i=1; i<=n; i++)
if(!dfn[i]) tarjan(i);
for(int u=1; u<=n; u++)
for(int i=head[u]; i; i=nxt[i]) {
int v=ver[i];
if(c[u]==c[v]) continue;
add_c(c[u],c[v]);
dr[c[v]]++;
}
for(int i=1; i<=scc; i++)
if(dr[i]==0) que[++tl]=i;
for(; hd<=tl; ) {
int u=que[hd++];
ans[u]+=val[u];
for(int i=hc[u]; i; i=nc[i]) {
int v=vc[i];
ans[v]=max(ans[v],ans[u]);
dr[v]--;
if(dr[v]==0) que[++tl]=v;
}
}
for(int i=1; i<=n; i++)
mx=max(mx,ans[i]);
printf("%d\n",mx);
return 0;
}
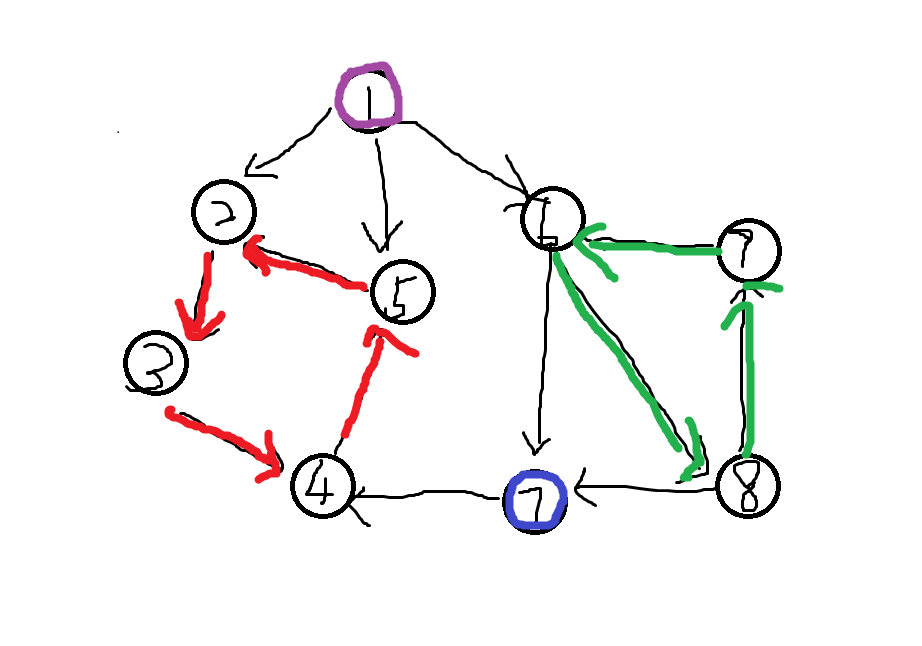
在这个图中,有四个强联通分量,为 \(\{1\},\{7\},\{2,3,4,5\},\{6,8,9\}\).
算法的注意事项
注意孤立点,重边,自环等。
应用
P5058 [ZJOI2004]嗅探器
只需要在 Tarjan 求割点时加上一些判断即可。
从 \(A\) 开始,\(B\) 一定在 \(A\) 其中一个子树。
若 \((u,v)\) 满足割点判定条件,再判断是否有 \(dfn_B\ge dfn_v\) 即可。
若 \(dfn_B\ge dfn_v\),则 \(B\) 一定在 \(v\) 下面。
code
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10,M=5e5+10;
int head[N],ver[2*M],nxt[2*M],tot=1;
int n,m,dfn[N],low[N],cut[N],num,ans;
int A,B;
void addedge(int x,int y) {
ver[++tot]=y;
nxt[tot]=head[x];
head[x]=tot;
}
void tarjan(int u,int in_edge) {
low[u]=dfn[u]=++num;
for(int i=head[u]; i; i=nxt[i]) {
int v=ver[i];
if(dfn[v]) {
if(i!=(in_edge^1))
low[u]=min(low[u],dfn[v]);
} else {
tarjan(v,i);
low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u]&&u!=A&&dfn[B]>=dfn[v])
cut[u]=1;
}
}
}
int main() {
scanf("%d",&n);
for(int u,v; ;) {
scanf("%d%d",&u,&v);
if(u==0&&v==0) break;
else m++;
addedge(u,v); addedge(v,u);
}
scanf("%d%d",&A,&B);
tarjan(A,0);
for(int i=1; i<=n; i++) {
if(cut[i]) return printf("%d\n",i),0;
}
puts("No solution");
return 0;
}
P2860 [USACO06JAN]Redundant Paths G
结论题,答案为缩点后叶子节点数除以 \(2\) 向上取整。
注意这里叶子指的是度数为 \(1\) 的点。
code
#include<bits/stdc++.h>
using namespace std;
const int N=5050,M=10050;
int n,m,head[N],nxt[2*M],ver[2*M],tot=1;
int dfn[N],low[N],num,dcc,c[N];
bool bri[2*M];
int leaf,deg[N];
void addedge(int u,int v) {
ver[++tot]=v;
nxt[tot]=head[u];
head[u]=tot;
}
void tarjan(int u,int in_edge) {
dfn[u]=low[u]=++num;
for(int i=head[u]; i; i=nxt[i]) {
int v=ver[i];
if(!dfn[v]) {
tarjan(v,i);
low[u]=min(low[u],low[v]);
if(low[v]>dfn[u]) bri[i]=bri[i^1]=true;
} else if(i!=(in_edge^1)) low[u]=min(low[u],dfn[v]);
}
}
void dfs(int u) {
c[u]=dcc;
for(int i=head[u]; i; i=nxt[i]) {
int v=ver[i];
if(c[v]||bri[i]) continue;
dfs(v);
}
}
int main() {
scanf("%d%d",&n,&m);
for(int i=1,u,v; i<=m; i++) {
scanf("%d%d",&u,&v);
addedge(u,v); addedge(v,u);
}
tarjan(1,0);
for(int i=1; i<=n; i++)
if(!c[i]) ++dcc,dfs(i);
for(int i=1; i<=m; i++)
if(bri[i<<1]) {
int u=ver[i<<1],v=ver[i<<1|1];
deg[c[u]]++; deg[c[v]]++;
}
for(int i=1; i<=dcc; i++) if(deg[i]==1) leaf++;
printf("%d\n",(leaf+1)/2);
return 0;
}
CF555E Case of Computer Network
若 \(s,t\) 在同一强连通分量内,一个强连通分量必存在环,环按同一方向定向即可。
若不在,则先缩点,形成树,然后染色判断即可。
code
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10,logn=20;
int n,m,q,tot=1,head[N],ver[2*N],nxt[2*N],rt,num;
int c[N],dcc;
int dfn[N],low[N];
bool brg[2*N];
int tc=1,hc[N],vc[2*N],nc[2*N];
int f[N][logn],depth[N],in[N];
int g[N][2];
int vis[N];
bool ok;
void addedge(int x,int y) {
ver[++tot]=y;
nxt[tot]=head[x];
head[x]=tot;
}
void addc(int x,int y) {
vc[++tc]=y;
nc[tc]=hc[x];
hc[x]=tc;
}
void tarjan(int u,int in_edge) {
in[u]=rt;
low[u]=dfn[u]=++num;
for(int i=head[u]; i; i=nxt[i]) {
int v=ver[i];
if(!dfn[v]) {
tarjan(v,i);
low[u]=min(low[u],low[v]);
if(low[v]>dfn[u]) {
brg[i]=brg[i^1]=true;
}
} else if(i!=(in_edge^1)) {
low[u]=min(low[u],dfn[v]);
}
}
}
void dfs(int u) {
c[u]=dcc;
for(int i=head[u]; i; i=nxt[i]) {
int v=ver[i];
if(c[v]||brg[i]) continue;
dfs(v);
}
}
void dfs2(int u,int father) {
f[u][0]=father; depth[u]=depth[father]+1;
for(int i=1; i<logn; i++) f[u][i]=f[f[u][i-1]][i-1];
for(int i=hc[u]; i; i=nc[i]) {
int v=vc[i];
if(v==father) continue;
dfs2(v,u);
}
}
int Lca(int u,int v) {
if(depth[v]>depth[u]) swap(u,v);
for(int i=logn-1; i>=0; i--) {
if(depth[f[u][i]]>=depth[v]) u=f[u][i];
}
if(u==v) return u;
for(int i=logn-1; i>=0; i--) {
if(f[u][i]!=f[v][i]) u=f[u][i],v=f[v][i];
}
return f[u][0];
}
void solve(int u,int father) {
vis[u]=1;
for(int i=hc[u]; i; i=nc[i]) {
int v=vc[i];
if(v==father) continue;
solve(v,u);
g[u][0]+=g[v][0]; g[u][1]+=g[v][1];
}
if(g[u][0]&&g[u][1]) ok=0;
}
int main() {
scanf("%d%d%d",&n,&m,&q);
for(int i=1,u,v; i<=m; i++) {
scanf("%d%d",&u,&v);
addedge(u,v); addedge(v,u);
}
for(int i=1; i<=n; i++)
if(!dfn[i]) rt=i,tarjan(i,0);
for(int i=1; i<=n; i++)
if(!c[i]) ++dcc,dfs(i);
for(int i=1; i<=m; i++) {
int u=c[ver[i<<1]],v=c[ver[i<<1|1]];
if(u==v) continue;
addc(u,v); addc(v,u);
}
for(int i=1; i<=dcc; i++) if(!depth[i]) rt=i,dfs2(i,0);
for(int i=1,u,v; i<=q; i++) {
scanf("%d%d",&u,&v);
if(in[u]!=in[v]) return puts("No"),0;
if(c[u]==c[v]) continue;
int lc=Lca(c[u],c[v]);
g[c[u]][0]+=1; g[lc][0]+=-1;
g[c[v]][1]+=1; g[lc][1]+=-1;
}
ok=1;
for(int i=1; i<=dcc; i++) if(!vis[i]) rt=i,solve(i,i);
puts(ok?"Yes":"No");
return 0;
}
P8867 [NOIP2022] 建造军营
发现跟边双有关,于是先缩点。(后述点全部是缩点后的)
然后设计一个树形 DP,设 \(1\) 为根.
设 \(f(u,0/1)\) 为 \(u\) 的子树下,选/不选军营的方案数。
为防止重复,我们强制 \(u\) 子树外的所有点都不建军营,并不选其它边。
设 \(E(u)\) 为 \(u\) 所含边数,\(V(u)\) 为所含点数。
我们考虑如何加入一个儿子 \(v\)。
\(f(u,0)=f(u,0)\cdot 2\cdot f(v,0)\)
\(f(u,1)=f(u,0)\cdot f(v,1)+f(u,1)\cdot (2f(v,0)+f(v,1))\).
初始时,\(f(u,0)=2^{E(u)},f(u,1)=2^{E(u)+V(u)}-f(u,0)\)
设 \(s(u)\) 为 \(u\) 子树内所有边。
最后合并答案,每个子树的贡献为 \(f(u,1)\cdot 2^{s(1)-s(u)-1}\).
特别的,\(1\) 的贡献为 \(f(u,1)\).
code
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+10,M=2e6+10;
const int mod=1e9+7;
int head[N],ver[M],nxt[M],tot=1;
int dfn[N],low[N];
int c[N],bri[M];
int n,m,num,dcc;
int V[N],E[N],s[N];
long long f[N][2],ans;
vector<int> e[N];
int qpow(int a,int b) {
int res=1;
for(; b; b>>=1) {
if(b&1) res=1ll*res*a%mod;
a=1ll*a*a%mod;
}
return res;
}
void addedge(int x,int y) {
ver[++tot]=y;
nxt[tot]=head[x];
head[x]=tot;
}
void tarjan(int u,int in_edge) {
dfn[u]=low[u]=++num;
for(int i=head[u]; i; i=nxt[i]) {
int v=ver[i];
if(!dfn[v]) {
tarjan(v,i);
low[u]=min(low[u],low[v]);
if(low[v]>dfn[u]) bri[i]=bri[i^1]=true;
} else if(i!=(in_edge^1)) low[u]=min(low[u],dfn[v]);
}
}
void dfs(int u) {
c[u]=dcc; V[dcc]++;
for(int i=head[u]; i; i=nxt[i]) {
int v=ver[i];
if(c[v]||bri[i]) continue;
dfs(v);
}
}
void dfs2(int u,int fa) {
s[u]=E[u];
for (int i=0; i<(int)e[u].size(); i++) {
int v=e[u][i];
if(v==fa) continue;
dfs2(v,u);
s[u]+=s[v]+1;
}
}
void solve(int u,int fa) {
f[u][0]=qpow(2,E[u]);
f[u][1]=qpow(2,E[u]+V[u])-f[u][0];
for(int i=0; i<(int)e[u].size(); i++) {
int v=e[u][i];
if(v==fa) continue;
solve(v,u);
f[u][1]=(f[u][1]*(((f[v][0]*2)+f[v][1])%mod)%mod+f[u][0]*f[v][1]%mod)%mod;
f[u][0]=f[u][0]*((f[v][0]*2)%mod)%mod;
}
if(u==1) ans=(ans+f[u][1])%mod;
else ans=(ans+f[u][1]*qpow(2,s[1]-s[u]-1))%mod;
}
int main() {
scanf("%d%d",&n,&m);
for(int i=1,u,v; i<=m; i++) {
scanf("%d%d",&u,&v);
addedge(u,v); addedge(v,u);
}
tarjan(1,0);
for(int i=1; i<=n; i++)
if(!c[i]) ++dcc,dfs(i);
for(int i=1; i<=m; i++) {
int u=ver[i<<1|1],v=ver[i<<1];
if(c[u]==c[v]) E[c[u]]++;
else e[c[u]].push_back(c[v]),e[c[v]].push_back(c[u]);
}
dfs2(1,0);
solve(1,0);
printf("%lld\n",ans);
return 0;
}


