笛卡尔树
引入
笛卡尔树是一种与堆和平衡树密切相关的数据结构。
笛卡尔树是一种二叉树,每个节点有两个值 \((k,w)\),
其中 \(k\) 满足二叉搜索树的性质, \(w\) 满足堆的性质。
期望的深度是 \(\log n\) 的。
三个性质:
- 任何子节点 \(w\) 满足小于(或大于)父节点的 \(w\)。
- 对于任何父节点,左儿子的 \(k\) 权值小于父节点 \(k\),右儿子 \(k\) 大于父节点 \(k\)。
- 若 \(k\) 值为数组下标,那么任意两个节点 \(u,v\) 的最近公共祖先的权值即为区间 \([u,v]\) 中的极值。
构建
构建笛卡尔树需要我们先构建小根堆。我们先将 \(k\) 值当作下标,把 \(w\) 值当作元素的权值。
我们还需要维护的是树的右链,即从根节点向右走构成的链。
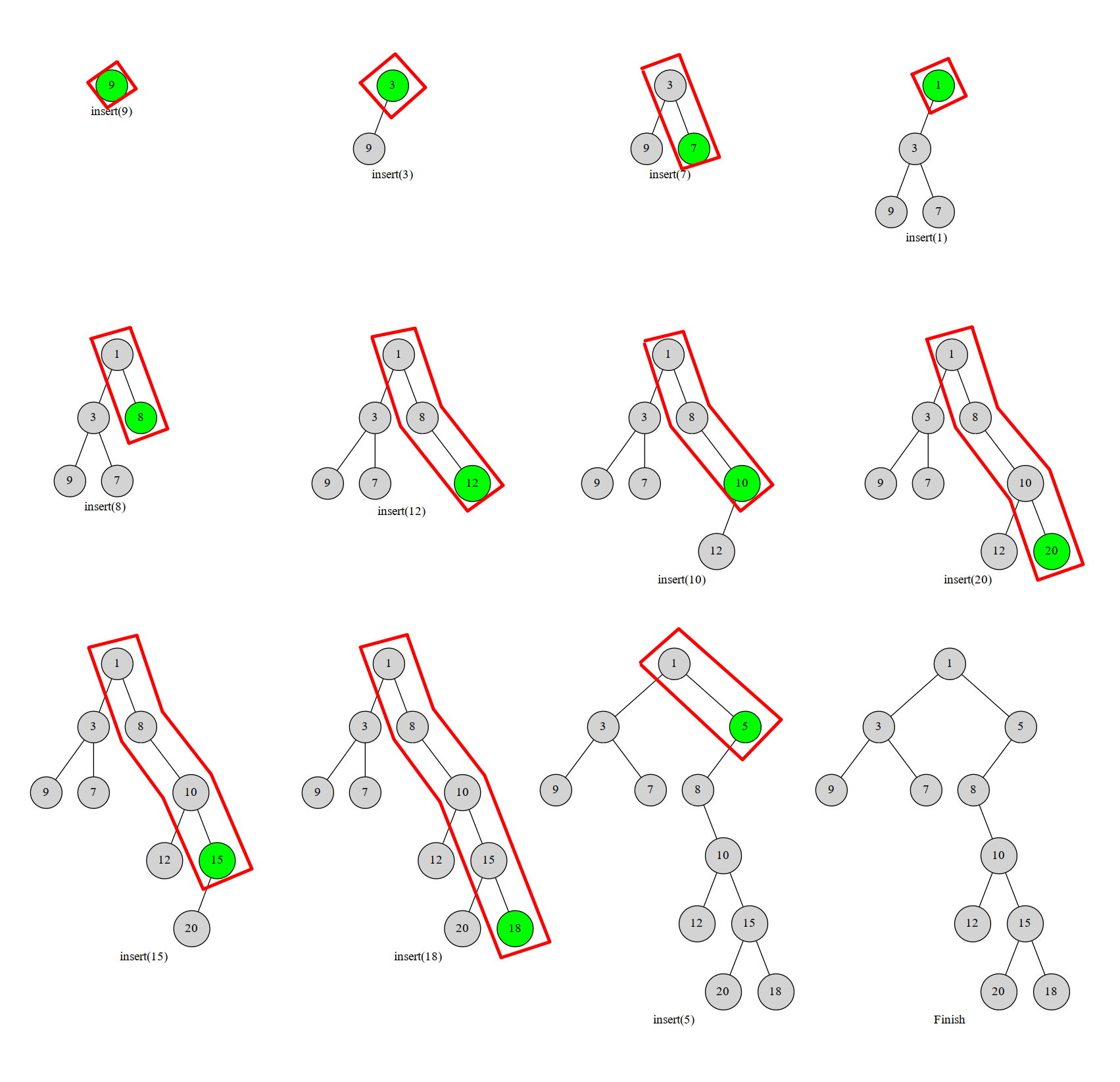
我们每次插入一个节点 \(u\) 都只需要在右链插入。我们从根节点开始,设当前到达的为 \(x\).如果找到第一个 \(x_w>u_w\) ,那么把 \(u\) 接在 \(fa_x\) 的右儿子,然后将 \(x\) 接在 \(u\) 的左儿子。总而言之,只要维护使得右链是单调的即可。
时间复杂度 \(O(n)\),因为我们维护的右链中,每个节点只会进出右链一次。
可以证明这样构建出的一定满足性质。
首先,我们是按 \(k\) 值排序后再插入的。在插入过程中,我们没有打乱它的中序遍历。所以满足二叉搜索树性质。
其次,我们的 \(w\) 值在插入的过程中,是不会出现不满足堆的性质的情况。
应用
Luogu P5854 【模板】笛卡尔树
我们构建一个小根笛卡尔树。
我们把数组下标作为 \(k\),值作为 \(w\).
我们维护一个单调栈,这个栈代表的是右链。
注意到右链是单调上升的。
当我们插入一个节点 \(u\) 时,
若单调栈末尾元素 \(x\) 满足,\(w_u<w_x\),弹出 \(x\),不断执行上述过程。
最后将 \(u\) 接在栈尾的右儿子上,再把最后一个出栈的元素接在 \(u\) 的左儿子。
构造完成后,stk[1] 为根节点。
code
#include<bits/stdc++.h>
using namespace std;
const int N=1e7+10;
int n,a[N],stk[N],ls[N],rs[N];
int tp;
int main() {
scanf("%d",&n);
for(int i=1; i<=n; i++) scanf("%d",&a[i]);
stk[++tp]=0;
for(int i=1; i<=n; i++) {
while(tp&&a[stk[tp]]>a[i]) ls[i]=stk[tp--];
if(stk[tp]) rs[stk[tp]]=i;
stk[++tp]=i;
}
long long L=0,R=0;
for(int i=1; i<=n; i++) {
L^=1ll*i*(ls[i]+1);
R^=1ll*i*(rs[i]+1);
}
printf("%lld %lld\n",L,R);
return 0;
}
Luogu 1377 树的序
题意:
给定键值 \(k_1,k_2,..k_n(1\le k_i\le n,k_i\not=k_j)\).
按要求建立一颗二叉树。
空树中加入一个键值 \(k\) ,则变为只有一个结点的二叉查找树,此结点的键值即为 \(k\)。
在非空树中插入一个键值 \(k\) ,若 \(k\) 小于其根的键值,则在其左子树中插入 \(k\) ,否则在其右子树中插入 \(k\) 。
求能建出同样二叉树的字典序最小的键值排列。
这道题其实是一个笛卡尔树。
满足平衡树性质的是 \(k\) 值,满足堆性质的是下标 \(i\).
于是建出的树实质上是笛卡尔树。
我们对笛卡尔树进行先序遍历,输出每个节点 \(k\) 值,即可求出结果。
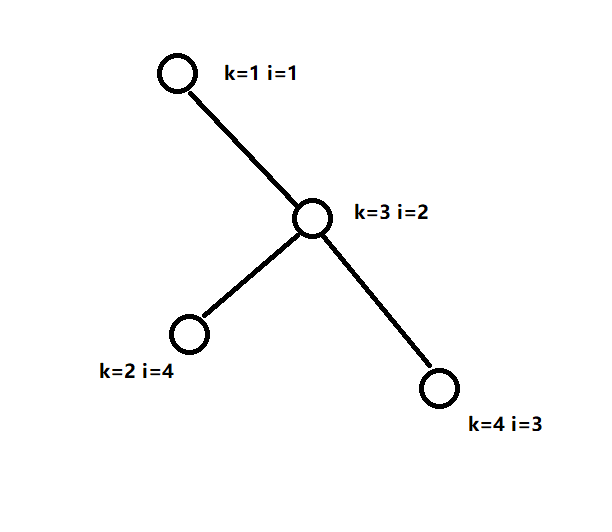
至于原因,我们依据样例解决。
如下图,由于无论是 \(k=2\) 先插入,或 \(k=4\) 先插入,
都不会发生变化。
而左子树比右子树 \(k\) 值小,所以先输出左子树。
code
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n,stk[N],tp,rs[N],ls[N],a[N];
void dfs(int u) {
if(u) {
printf("%d ",u);
dfs(ls[u]); dfs(rs[u]);
}
}
int main() {
scanf("%d",&n);
for(int i=1,x; i<=n; i++) {
scanf("%d",&x);
a[x]=i;
}
for(int i=1; i<=n; i++) {
while(tp&&a[stk[tp]]>a[i]) ls[i]=stk[tp--];
rs[stk[tp]]=i;
stk[++tp]=i;
}
dfs(stk[1]);
return 0;
}
Hdu 1506
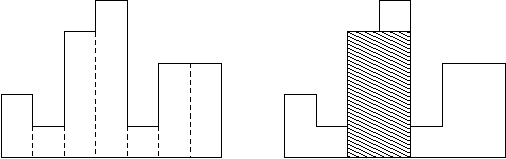
题意:\(n\) 个位置,每个位置上的高度是 \(h_i\),求最大子矩阵。
这是一个直方图
这道题可以使用笛卡尔树。
我们先构建笛卡尔树。
所以在已知节点 \(x\) 是某两点的最近公共祖先,\(x\) 的子树大小为 \(size_x\)。
该子树的答案为 \(x\times size_x\)。
原因是该子树内所有区间的最小值已经确定是 \(h_x\),所以要找到最长的区间。
注意到最长的区间即为 \(size_x\)。
所以我们要做的就是找到所有子树,比较 \(x\times size_x\)。
显然可以一遍深搜完成,时间复杂度 \(O(n)\)。
code
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int n,a[N],stk[N],ls[N],rs[N],siz[N],tp,rt,ans;
void dfs(int u) {
siz[u]=1;
if(ls[u]) {dfs(ls[u]); siz[u]+=siz[ls[u]];}
if(rs[u]) {dfs(rs[u]); siz[u]+=siz[rs[u]];}
ans=max(ans,siz[u]*a[u]);
}
int main() {
scanf("%d",&n);
for(int i=1; i<=n; i++) scanf("%d",&a[i]);
stk[++tp]=0;
for(int i=1; i<=n; i++) {
while(tp&&a[stk[tp]]>a[i]) ls[i]=stk[tp--];
if(stk[tp]) rs[stk[tp]]=i;
else rt=i;
stk[++tp]=i;
}
dfs(rt);
printf("%d\n",ans);
return 0;
}
Luogu P3793 由乃救爷爷
随机给出 \(q\) 个询问 RMQ. \(n,q\le 2*10^7\).
这时候就可以用到我们的笛卡尔树了.
我们直接从根节点开始搜索我们的 LCA.
由于编号有序,所以我们可以二分。
由于这题数据随机,所以单次复杂度极小,大概位于 \(O(\log n)-O(n)\) 间。
但实质使用起来常数极小。
有一种保险的办法,那就是用 tarjan 求 LCA.
code
#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
const int N=2e7+10;
int n,m,s,a[N],stk[N],ls[N],rs[N],tp;
ull ans;
namespace GenHelper {
unsigned z1,z2,z3,z4,b;
unsigned rand_() {
b=((z1<<6)^z1)>>13;
z1=((z1&4294967294U)<<18)^b;
b=((z2<<2)^z2)>>27;
z2=((z2&4294967288U)<<2)^b;
b=((z3<<13)^z3)>>21;
z3=((z3&4294967280U)<<7)^b;
b=((z4<<3)^z4)>>12;
z4=((z4&4294967168U)<<13)^b;
return (z1^z2^z3^z4);
}
}
void srand(unsigned x) {
using namespace GenHelper;
z1=x; z2=(~x)^0x233333333U; z3=x^0x1234598766U; z4=(~x)+51;
}
int read() {
using namespace GenHelper;
int a=rand_()&32767;
int b=rand_()&32767;
return a*32768+b;
}
int query(int l,int r) {
int rt=stk[1];
for(; ; ) {
if(l<=rt&&rt<=r) return a[rt];
if(rt<l) rt=rs[rt];
else rt=ls[rt];
}
}
int main() {
scanf("%d%d%d",&n,&m,&s);
srand(s);
for(int i=1; i<=n; i++) a[i]=read();
for(int i=1; i<=n; i++) {
while(tp&&a[stk[tp]]<a[i]) ls[i]=stk[tp--];
rs[stk[tp]]=i;
stk[++tp]=i;
}
for(int i=1,l,r; i<=m; i++) {
l=read()%n+1; r=read()%n+1;
if(l>r) swap(l,r);
ans=ans+query(l,r);
}
cout<<ans<<endl;
return 0;
}
Luogu P6453 PERIODNI
统计直方图中选出 \(k\) 个格子放置象棋中的车。
使得他们两两不攻击的方案数。
先构造一个小根的笛卡尔树。
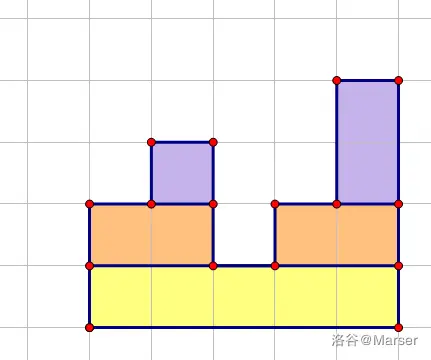
我们发现,这样构成的若干个矩形正好对应小根笛卡尔树上的所有节点,
每次递归处理的两个小联通块正是当前节点的两个儿子。
根据定义,对于节点 \(x\) 代表的矩形,长度为 \(siz_x\), 高度为 \(h_x-h_{fa}\)。
我们设计一个状态 \(f_{u,j}\) 表示在 \(u\) 的子树内选择了 \(j\) 个格子的方案数。
对于一个节点 \(x\) ,它儿子对它的贡献可以用树上背包来解决。
设 \(g_{u,j}\) 为左右儿子共选择了 j 个格子。
\(g_{u,j}=\sum f_{ls,o}*f_{rs,j-o}\)
现在我们合并儿子以及自己的贡献。
我们枚举 \(j\) 表示 \(u\) 子树(包括自己)总共选择了 \(j\) 个格子。
在枚举 \(o\) 表示 \(u\) 左右儿子(不包括自己)总共选择了 \(o\) 个格子。
为了使方程优化,我们令 \(H=h_x-h_{fa_x},S=siz_x\)
$f_{u,j}=\sum g_{u,o}\binom{S-o}{j-o}\binom{H}{j-o}(j-o)! $
答案是 \(f_{rt,k}\).
code
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL N=510,p=1e9+7;
LL n,k;
LL a[N];
LL stk[N],tp;
LL ls[N],rs[N],size[N];
LL f[N][N],g[N][N];
LL inv[1000010],mul1[1000010],mul2[1000010];
LL C(LL x,LL y) {return y>x?0:mul1[x]*mul2[y]%p*mul2[x-y]%p; }
void dfs(LL u,LL fa) {
if(ls[u]) dfs(ls[u],u);
if(rs[u]) dfs(rs[u],u);
size[u]=size[ls[u]]+size[rs[u]]+1;
for(LL i=0; i<=size[ls[u]]; i++) {
for(LL o=0; o<=size[rs[u]]; o++) {
g[u][i+o]+=f[ls[u]][i]*f[rs[u]][o]%p;
g[u][i+o]%=p;
}
}
for(LL i=0; i<=size[u]; i++) {
for(LL o=0; o<=i; o++) {
f[u][i]+=g[u][o]*(C(size[u]-o,i-o)*C(a[u]-a[fa],i-o)%p*mul1[i-o]%p)%p;
f[u][i]%=p;
}
}
}
int main() {
scanf("%lld%lld",&n,&k);
inv[0]=mul1[0]=mul2[0]=inv[1]=mul1[1]=mul2[1]=1;
for(LL i=2; i<=1000000; i++) {
inv[i]=inv[p%i]*(p-p/i)%p;
mul1[i]=mul1[i-1]*i%p;
mul2[i]=mul2[i-1]*inv[i]%p;
}
for(LL i=1; i<=n; i++) {
scanf("%lld",&a[i]);
while(tp&&a[stk[tp]]>a[i]) ls[i]=stk[tp--];
rs[stk[tp]]=i;
stk[++tp]=i;
}
f[0][0]=1;
dfs(stk[1],0);
printf("%lld\n",f[stk[1]][k]);
return 0;
}
Hdu 6305
定义两个数列同构是对于任意子区间他们的 RMQ 位置一样。
已知 \(A\) 数列,\(B\) 的数列每个数在 \([0,1)\) 实数集中随机。
若不同构 \(w_B=0\). 若同构 \(w_B=\sum B_i\).
求 \(w_B\) 期望。
容易发现,同构其实是指笛卡尔树同构。
对于每个子树,其同构的概率是 \(\dfrac{1}{siz}\).
如不限制条件,对于 \(w_B\) 的期望为 \(\dfrac{1}{2}n\).
则最终答案是 \(\dfrac{1}{2}n\cdot \dfrac{1}{\prod siz_u}\)
code
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=1e6+10;
const LL mod=1e9+7;
int t,n,q,ls[N],rs[N],stk[N],tp,siz[N],a[N];
LL inv[N],ans;
void dfs(int u) {
siz[u]=1;
if(ls[u]) {dfs(ls[u]); siz[u]+=siz[ls[u]];}
if(rs[u]) {dfs(rs[u]); siz[u]+=siz[rs[u]];}
ans=ans*inv[siz[u]]%mod;
}
int main() {
inv[1]=1;
for(int i=2; i<N; i++)
inv[i]=inv[mod%i]*(mod-mod/i)%mod;
scanf("%d",&q);
for(; q; q--) {
tp=0;
scanf("%d",&n);
ans=n*inv[2]%mod;
for(int i=1; i<=n; i++) {
scanf("%d",&a[i]);
ls[i]=rs[i]=0;
}
for(int i=1; i<=n; i++) {
while(tp&&a[stk[tp]]<a[i]) ls[i]=stk[tp--];
rs[stk[tp]]=i;
stk[++tp]=i;
}
dfs(stk[1]);
printf("%lld\n",ans);
}
return 0;
}
P3246 序列
题意:一个序列,每次询问截取一个区间,求这个区间所有子区间中的最小值之和。\(n\le 10^5\)
看到最小值,考虑建立笛卡尔树。
当我们建立了笛卡尔树后,
我们发现,对于任意一个节点,它的子树所有点代表一个区间,这个区间内的数都以它为最小值。
我们取出区间 \([L,R]\) 的最小值,所在位置是 \(p\),然后这个区间分成了两半。
这里用笛卡尔树来求,虽然理论是 \(O(\log n)\),但实际极快。
考虑分治。
对于横跨两个区间的所有子区间,他们的总贡献是 \(a_p*(p-L+1)*(R-p+1)\).
剩下两个区间怎么求呢?注意有一点,不能再次分治,请自行思考。
我们用笛卡尔树先预处理 \(pre_i,suf_i\),代表向前,向后第一个比 \(a_i\) 小的位置。
其实就是笛卡尔树中一个节点覆盖的区间。
再处理 \(fr_i,fl_i\) 表示向右/左递推,以 \(i\) 结尾的区间贡献。
\(fr_i=fr_{pre_i}+(i-pre_i)\cdot a_i\).
\(fl_i=fl_{suf_i}+(suf_i-i)\cdot a_i\).
再处理 \(gr,gl\) 表示前缀,后缀和。
左边的贡献是 \(gr_R-gr_p-fr_p\cdot (R-p)\).
右边的贡献是 \(gl_L-gl_p-fl_p\cdot (p-L)\).
左边+右边+横跨 即为答案。
时间复杂度 \(O(n+kq)\),其中 \(k\) 是用笛卡尔树求解 RMQ 的常数,
可看做 \(k\le \log n\).
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+10;
int q,n,tp,a[N],st[N],ls[N],rs[N],rt;
int suf[N],pre[N],fr[N],fl[N],gr[N],gl[N];
int query(int l,int r) {
for(int u=rt; ;) {
if(l<=u&&u<=r) return u;
u=u>r?ls[u]:rs[u];
}
}
signed main() {
scanf("%lld%lld",&n,&q);
for(int i=1; i<=n; i++) scanf("%lld",&a[i]);
for(int i=1; i<=n; i++) {
while(tp&&a[st[tp]]>a[i]) ls[i]=st[tp--];
rs[st[tp]]=i; st[++tp]=i;
}
rt=st[1]; tp=0;
for(int i=1; i<=n; i++) {
while(tp&&a[st[tp]]>a[i]) suf[st[tp--]]=i;
pre[i]=st[tp]; st[++tp]=i;
}
while(tp) {pre[st[tp]]=st[tp-1]; suf[st[tp--]]=n+1;}
for(int i=1; i<=n; i++) {
fr[i]=fr[pre[i]]+a[i]*(i-pre[i]);
gr[i]=gr[i-1]+fr[i];
}
for(int i=n; i>=1; i--) {
fl[i]=fl[suf[i]]+a[i]*(suf[i]-i);
gl[i]=gl[i+1]+fl[i];
}
for(int l,r; q; q--) {
scanf("%lld%lld",&l,&r);
int p=query(l,r);
printf("%lld\n",(p-l+1)*(r-p+1)*a[p]+gr[r]-gr[p]-fr[p]*(r-p)+gl[l]-gl[p]-fl[p]*(p-l));
}
return 0;
}
CF1156E
题意:求多少个区间满足 \(a_L+a_R=max(a_{[L,R]})\).
考虑笛卡尔树上启发式合并。
对于一个笛卡尔树上的节点,考虑在它左右子树内各取一数构成区间。
用 STL set,来解决匹配问题。
设左子树为 \(A\) 集合,右子树为 \(B\) 集合。
若 \(|A|>|B|\),交换 \(A,B\).
则 \(|A|<|B|\). 将 \(B\) 所有元素放进 \(set\).
让 \(A\) 去匹配。
这样启发式合并是一只 \(log\) 的。
加上 set 一只 \(log\).
递归笛卡尔树上所有节点,诸如这样合并.
总复杂度 \(O(n\log^2 n)\).
code
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;
int n,a[N],ls[N],rs[N],st[N],tp,rt;
set<int> s[N];
int ans=0;
void merge(int i,int j) {
if(s[j].size()>s[i].size()) swap(s[i],s[j]);
for(auto v:s[j])
if(s[i].find(a[i]-v)!=s[i].end()) ans++;
for(auto v:s[j])
s[i].insert(v);
}
void dfs(int u) {
if(ls[u]) {
dfs(ls[u]);
merge(u,ls[u]);
}
if(rs[u]) {
dfs(rs[u]);
merge(u,rs[u]);
}
s[u].insert(a[u]);
}
signed main() {
scanf("%d",&n);
for(int i=1; i<=n; i++) scanf("%d",&a[i]);
for(int i=1; i<=n; i++) {
while(tp&&a[st[tp]]<a[i]) ls[i]=st[tp--];
if(st[tp]) rs[st[tp]]=i;
st[++tp]=i;
}
rt=st[1];
dfs(rt);
printf("%d\n",ans);
return 0;
}


