斜率优化
P3195 [HNOI2008]玩具装箱
原始方程 \(dp_i=\min(dp_j+(sum_i+i-sum_j-j-L-1)^2)\).
我们设 \(a_i=sum_i+i\)
\(b_i=sum_j+j+L+1\)
\(dp_i=\min(dp_j+(a_i-b_j)^2)\)
设\(dp_i\) 由 \(dp_j\) 转移而来。
\(dp_i=dp_j+a_i^2-2a_ib_j+b_j^2\)
写成一次函数在y轴截距形式:
\(dp_i-a_i^2=dp_j+b_j^2-2a_ib_j\)
其中\(dp_i-a_i^2\) 为截距, \(b_j\) 为 横坐标 \(dp_j+b_j^2\) 为 纵坐标, \(2a_i\) 为 斜率.
即求最小的截距。
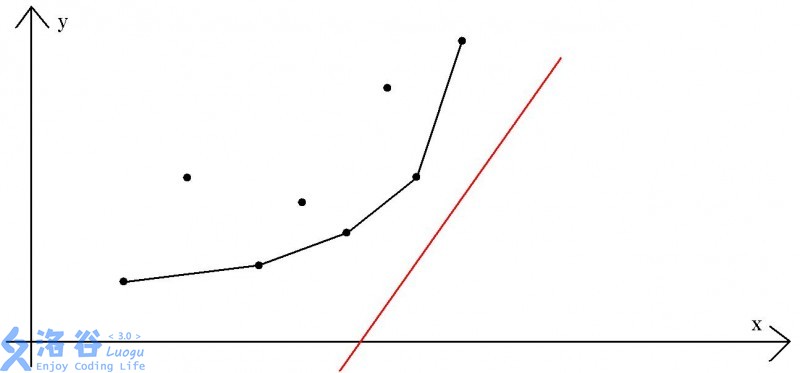
红线为斜率为 \(2a_i\) 的直线。
从下往上移动,碰到第一个点为\(j\).
这时就求得了最小的截距。
\(j\)与\(j-1\)的斜率是不超过 \(2a_i\) 最大的。
于是用单调队列维护凸包。
凸包内的点是不用考虑的。
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
typedef double db;
typedef long long LL;
const int N=50010;
int n,L;
db sum[N],dp[N];
int head,tail,Q[N];
db a(int i) {return sum[i]+i;}
db b(int i) {return a(i)+L+1;}
db X(int i) {return b(i);}
db Y(int i) {return dp[i]+b(i)*b(i);}
db slope(int i,int j) {return (Y(i)-Y(j))/(X(i)-X(j));}
int main() {
scanf("%d%d",&n,&L);
for(int i=1; i<=n; i++) {
scanf("%lf",&sum[i]);
sum[i]+=sum[i-1];
}
head=tail=1;
for(int i=1; i<=n; i++) {
while(head<tail&&slope(Q[head],Q[head+1])<2*a(i)) ++head;
dp[i]=dp[Q[head]]+(a(i)-b(Q[head]))*(a(i)-b(Q[head]));
while(head<tail&&slope(i,Q[tail-1])<slope(Q[tail-1],Q[tail])) --tail;
Q[++tail]=i;
}
printf("%lld\n",(LL)dp[n]);
return 0;
}
P2900 [USACO08MAR]Land Acquisition G
先将所有没用的土地筛选掉,即把那些能被更大的土地包含的筛掉。
剩下土地排序,就有了高度递减,宽度递增的土地。
\(f_i=\max(f_j+h_{j+1}w_i)\).
\(f_j=f_i+w_i(-h_{j+1})\).
就写成了一次函数式,最小化截距即可。
维护下凸包。

#include<algorithm>
#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
typedef long long int64;
typedef double db;
const int64 N=5e4+10,inf=2e12;
struct land {int64 h,w;} a[N];
int n,q[N],head,tail,m;
db f[N],fw;
int64 X(int i) {return -a[i+1].h;}
int64 Y(int i) {return f[i];}
db slope(int i,int j) {return 1.0*(Y(i)-Y(j))/(X(i)-X(j));}
bool cmp(land s,land t) {return s.h==t.h?s.w>t.w:s.h>t.h;}
int main() {
freopen("data.in","r",stdin);
scanf("%d",&n);
for(int i=1; i<=n; i++) cin>>a[i].h>>a[i].w;
sort(a+1,a+1+n,cmp);
for(int i=1; i<=n; i++)
if(a[i].w>a[m].w)
a[++m]=a[i];
head=1; tail=0; q[++tail]=0;
for(int i=1; i<=m; i++) {
while(head<tail&&slope(q[head],q[head+1])<=a[i].w) head++;
f[i]=f[q[head]]+a[q[head]+1].h*a[i].w;
while(head<tail&&slope(q[tail],q[tail-1])>=slope(i,q[tail])) tail--;
q[++tail]=i;
}
printf("%lld\n",(int64)f[m]);
return 0;
}
P4360 [CEOI2004] 锯木厂选址
设 \(all\) 为所有树运到山脚的总价格, \(dis_i\)为第 \(i\) 棵树到山脚的距离, \(sum_i\) 表示从山顶到这棵树的所有重量和。
\(f_i\) 为在 \(i\) 建立第二个锯木厂的最小价格。
\(f_i=all-dis_j \times sum_j-dis_i \times (sum_i-sum_j)\)
移项得到 \(f_i-all+dis_i\times sum_i=-dis_j\times sum_j+dis_i\times sum_j\)
放入坐标系 \(x=-sum_j,y=-dis_j\times sum_j,k=dis_i\)
最小化截距,维护上凸包。

#include<algorithm>
#include<cstdio>
#include<iostream>
using namespace std;
typedef double db;
const int N=20010;
int n,head,tail,q[N];
double w[N],d[N],dis[N],sum[N],f[N],all,ans=2e9;
//fi-all+dis[i]*sum[i]=dis[j]*sum[j]+dis[i]*sum[j]
db X(int i) {return sum[i];}
db Y(int i) {return dis[i]*sum[i];}
db slope(int i,int j) {return (Y(i)-Y(j))/(X(i)-X(j));}
int main() {
scanf("%d",&n);
for(int i=1; i<=n; i++) scanf("%lf%lf",&w[i],&d[i]);
for(int i=n; i>=1; i--) dis[i]=dis[i+1]+d[i];
for(int i=1; i<=n; i++) sum[i]=sum[i-1]+w[i];
for(int i=1; i<=n; i++) all+=w[i]*dis[i];
head=1; tail=0;
for(int i=1; i<=n; i++) {
while(head<tail&&slope(q[head],q[head+1])>=dis[i]) head++;
int j=q[head]; f[i]=all-dis[j]*sum[j]-dis[i]*(sum[i]-sum[j]);
while(head<tail&&slope(q[tail],q[tail-1])<=slope(q[tail],i)) tail--;
q[++tail]=i;
}
for(int i=1; i<=n; i++) ans=min(ans,f[i]);
printf("%d\n",(int)ans);
return 0;
}
P5785 [SDOI2012]任务安排
这里采用一种叫费用提前计算的方法计算价格。
\(c\) 数组为费用前缀和, \(t\) 数组为时间前缀和。
\(f_i=\min(f_j+t_i \times (c_i-c_j)+s\times (c_n-c_j))\)
即把 \(s\) 的贡献提前计算了,不然还要带另一维 \(m\).
\(f_i-t_i\times c_i-s\times c_n=f_j-(s+t_i)\times c_j\)
左式为截距,最小化截距即可。
\(x=c_j,k=s+t_i,y=f_j\).
复杂度\(O(n)\)
#include<algorithm>
#include<cstdio>
#include<iostream>
using namespace std;
typedef double db;
const int N=2e5+10;
int n,q[N],head,tail;
db s,w[N],d[N],c[N],t[N],f[N];
//f[i] = f[j] +t[i] * (c[i]-c[j]) + S*(c[n]-c[j])
//f[i]-t[i]*c[i]-s*c[n]=f[j]-(s+t[i])*c[j]
db X(int i) {return c[i];}
db Y(int i) {return f[i];}
db slope(int i,int j) {return (Y(i)-Y(j))/(X(i)-X(j));}
int main() {
scanf("%d%lf",&n,&s);
for(int i=1; i<=n; i++) {
scanf("%lf%lf",&d[i],&w[i]);
c[i]=c[i-1]+w[i];
t[i]=t[i-1]+d[i];
}
head=1; tail=0; q[++tail]=0;
for(int i=1; i<=n; i++) {
while(head<tail&&slope(q[head],q[head+1])<=s+t[i]) head++;
int j=q[head]; f[i]=f[j]-(s+t[i])*c[j]+c[i]*t[i]+s*c[n];
while(head<tail&&slope(q[tail],q[tail-1])>=slope(i,q[tail-1])) tail--;
q[++tail]=i;
}
printf("%lld\n",(long long)f[n]);
return 0;
}
但是因为本题有负数, \(s+t_i\) 不具有单调性,所以队头不能出队了。
同样维护下凸壳,要用二分查找。
#include<algorithm>
#include<cstdio>
#include<iostream>
using namespace std;
typedef double db;
const int N=3e5+10;
int n,q[N],head,tail;
db s,w[N],d[N],c[N],t[N],f[N];
//f[i] = f[j] +t[i] * (c[i]-c[j]) + S*(c[n]-c[j])
//f[i]-t[i]*c[i]-s*c[n]=f[j]-(s+t[i])*c[j]
db X(int i) {return c[i];}
db Y(int i) {return f[i];}
db slope(int i,int j) {return (Y(i)-Y(j))/(X(i)-X(j));}
int search(int i,db k) {
if(head==tail) return q[head];
int l=head,r=tail;
while(l<r) {
int mid=(l+r)/2;
if(slope(q[mid+1],q[mid])<=k) l=mid+1;
else r=mid;
}
return q[l];
}
int main() {
scanf("%d%lf",&n,&s);
for(int i=1; i<=n; i++) {
scanf("%lf%lf",&d[i],&w[i]);
c[i]=c[i-1]+w[i];
t[i]=t[i-1]+d[i];
}
head=1; tail=0; q[++tail]=0;
for(int i=1; i<=n; i++) {
// while(head<tail&&slope(q[head],q[head+1])<=s+t[i]) head++;
int j=search(i,s+t[i]);
f[i]=f[j]+t[i]*(c[i]-c[j])+s*(c[n]-c[j]);
while(head<tail&&slope(q[tail],q[tail-1])>=slope(i,q[tail-1])) tail--;
q[++tail]=i;
}
printf("%lld\n",(long long)f[n]);
return 0;
}


