树链剖分





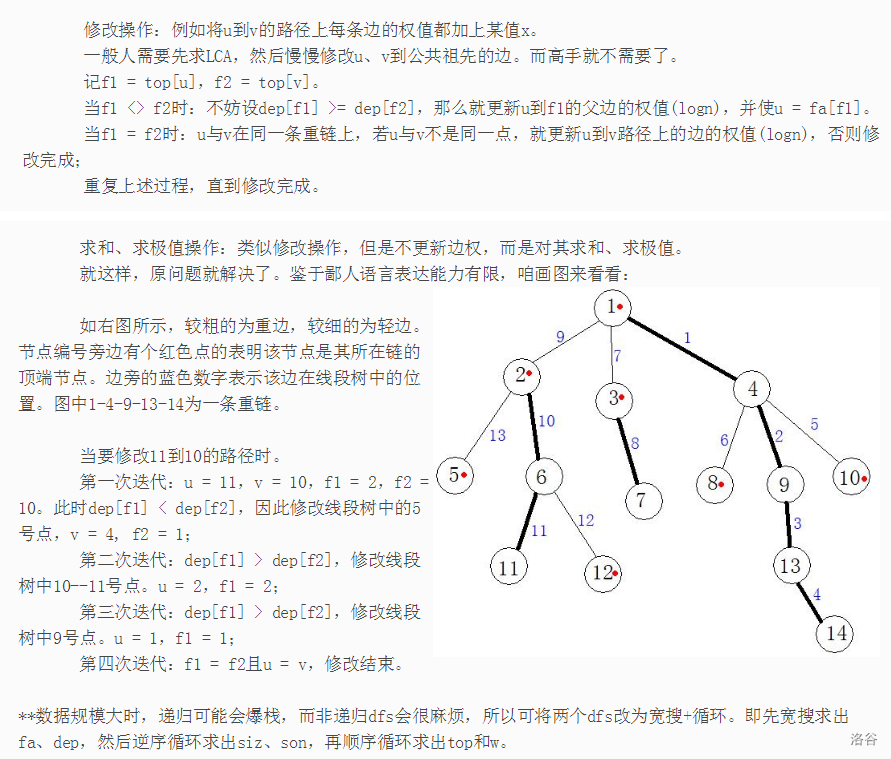
我们是怎么处理一条路径的呢?设这条路径端点是\(u,v\),那么我们就可以把它当做\(u-LCA(u,v)\)和\(LCA(u,v)-v\)。
我们从端点开始,往LCA跳。
如果跳到轻边,直接处理即可,因为一条轻边两端一定有重边。
如果跳到重边,就用线段树维护一下,因为重边的下标一定在线段树中是连续的,跳到重链的顶端节点。

如图(红色为重边):
路径的处理为8,6,5,1-3。
其中6,1-3用线段树维护,因为是重边
#include<bits/stdc++.h>
const int N=1e5+10;
using LL=long long;
using namespace std;
int n,q,rt;
LL w[N];
int fa[N],dep[N],siz[N],son[N],top[N],id[N],rid[N],num;
int head[N],ver[2*N],nxt[2*N],tot;
LL dat[4*N],tag[4*N],mod;
void addedge(int u,int v) {
ver[++tot]=v;
nxt[tot]=head[u];
head[u]=tot;
}
void build(int p,int l,int r) {
if(l==r) {
dat[p]=w[rid[l]]%mod;
return ;
}
int mid=(l+r)/2;
build(p*2,l,mid); build(p*2+1,mid+1,r);
dat[p]=(dat[p*2]+dat[p*2+1])%mod;
}
void pushdown(int p,int l,int r) {
int mid=(l+r)/2;
if(!tag[p]) return ;
tag[p*2]+=tag[p]; dat[p*2]+=1ll*(mid-l+1)*tag[p];
tag[p*2+1]+=tag[p]; dat[p*2+1]+=1ll*(r-mid)*tag[p];
tag[p*2]%=mod; tag[p*2+1]%=mod;
dat[p*2]%=mod; dat[p*2+1]%=mod;
tag[p]=0;
}
void modify(int p,int l,int r,int x,int y,LL k) {
if(x<=l&&r<=y) {
tag[p]+=k; tag[p]%=mod;
dat[p]+=1ll*(r-l+1)*k; dat[p]%=mod;
return ;
}
int mid=(l+r)/2;
pushdown(p,l,r);
if(x<=mid) modify(p*2,l,mid,x,y,k);
if(y>mid) modify(p*2+1,mid+1,r,x,y,k);
dat[p]=(dat[p*2]+dat[p*2+1])%mod;
}
LL query(int p,int l,int r,int x,int y) {
if(x<=l&&r<=y)
return dat[p];
int mid=(l+r)/2; LL res=0;
pushdown(p,l,r);
if(x<=mid) res+=query(p*2,l,mid,x,y);
if(y>mid) res+=query(p*2+1,mid+1,r,x,y);
return res%mod;
}
void dfs1(int u,int f) {
int maxsiz=-1;
siz[u]=1; dep[u]=dep[f]+1; fa[u]=f;
for(int i=head[u]; i; i=nxt[i]) {
int v=ver[i];
if(v==f) continue;
dfs1(v,u);
siz[u]+=siz[v];
if(siz[v]>maxsiz) {
maxsiz=siz[v];
son[u]=v;
}
}
}
void dfs2(int u,int f) {
top[u]=f;
id[u]=++num; rid[num]=u;
if(!son[u]) return ;
dfs2(son[u],f);
for(int i=head[u]; i; i=nxt[i]) {
int v=ver[i];
if(v==fa[u]||v==son[u]) continue;
dfs2(v,v);
}
}
void modify_son(int u,LL w) {
modify(1,1,n,id[u],id[u]+siz[u]-1,w);
}
LL query_son(int u) {
return query(1,1,n,id[u],id[u]+siz[u]-1);
}
void modify_chain(int u,int v,LL w) {
for(; top[u]!=top[v]; ) {
if(dep[top[u]]<dep[top[v]]) swap(u,v);
modify(1,1,n,id[top[u]],id[u],w);
u=fa[top[u]];
}
if(dep[u]>dep[v]) swap(u,v);
modify(1,1,n,id[u],id[v],w);
}
LL query_chain(int u,int v) {
LL ans=0;
for(; top[u]!=top[v]; ) {
if(dep[top[u]]<dep[top[v]]) swap(u,v);
ans+=query(1,1,n,id[top[u]],id[u]);
ans%=mod;
u=fa[top[u]];
}
if(dep[u]>dep[v]) swap(u,v);
ans+=query(1,1,n,id[u],id[v]);
return ans%mod;
}
int main() {
scanf("%d%d%d%lld",&n,&q,&rt,&mod);
for(int i=1; i<=n; i++) scanf("%lld",&w[i]);
for(int i=1,u,v; i<n; i++) {
scanf("%d%d",&u,&v);
addedge(u,v); addedge(v,u);
}
dfs1(rt,0); dfs2(rt,rt);
build(1,1,n);
for(LL op,e1,e2,e3; q; q--) {
scanf("%lld",&op);
if(op==1) {
scanf("%lld%lld%lld",&e1,&e2,&e3);
modify_chain(e1,e2,e3%mod);
} else if(op==2) {
scanf("%lld%lld",&e1,&e2);
printf("%lld\n",query_chain(e1,e2));
} else if(op==3) {
scanf("%lld%lld",&e1,&e3);
modify_son(e1,e3%mod);
} else {
scanf("%lld",&e1);
printf("%lld\n",query_son(e1));
}
}
return 0;
}
`

