第3章 矿物的分离特性与分选效果分析
-
矿物颗粒的几何特性
-
颗粒粒度大小的表示
演算直径表示方法
-
三轴径：长方体的长宽高（\(\mbox{Length}\)，\(\mbox{Breadth}\)，\(\mbox{Height}\)）；
序号 计算式 名称 意义 1 \(\frac{l+b}{2}\) 二轴平均径 显微镜下出现的颗
粒基本大小的投影2 \(\frac{l+b+h}{3}\) 三轴平均径 算术平均 3 \(\frac{3}{\frac{1}{l}+\frac{1}{b}+\frac{1}{h}}\) 三轴调和平均径 与颗粒比表面积相关 4 \(\sqrt{l\times b}\) 二轴几何平均径 接近于颗粒投
影面积的度量5 \(\sqrt[3]{l\times b\times h}\) 三轴几何平均径 假象等体积
正方体边长6 \(\sqrt{\frac{2(l\times b+l\times h+b\times h)}{6}}\) 假象等表面积
正方体的边长 -
球当量径：把颗粒看做相当的球；
-
与颗粒同体积的球的直径：等体积球当量径；
\[d_v=\sqrt[3]{\frac{6v}{\pi}} \] -
与颗粒同表面积的球直径：等表面积球当量径；
\[d_v=\sqrt{\frac{S}{\pi}} \]
-
-
圆当量径：与颗粒投影面积相等的圆直径；
\[d_H=\sqrt{\frac{4A}{\pi}} \] -
统计直径（定向径）：平行于一定方向（用显微镜）测得的线度；
-
马丁直径（Martin）：沿一定方向将投影面积等分的线段长度；
-
弗雷特直径（Feret）：沿一定方向测量颗粒投影轮廓平行线间距；
-
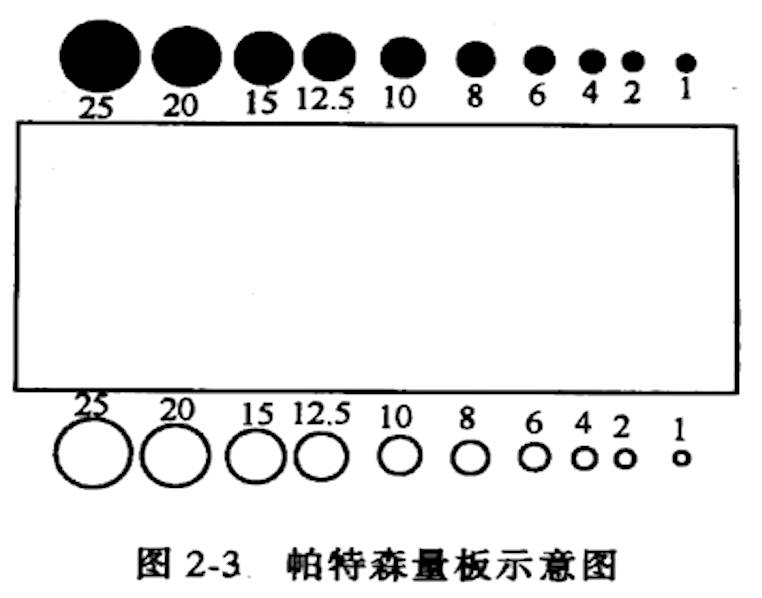
帕特森量板测定法：用一块玻璃量板代替线性目镜微标尺，把各个颗粒的投影面积与相应的圆圈比较，得出投影直径；
-
-
颗粒当量直径的定义
符号 名称 定义 公式 \(d_V\) 体积直径 与颗粒具有相同体积的圆球直径 \(V=\frac{\pi}{6}d^{3}_{V}\) \(d_S\) 面积直径 与颗粒具有相同的表面积的圆球直径 \(S=\pi{d^2_S}\) \(d_{SV}\) 面积体积直径 与颗粒具有相同外表面和体积比的圆球直径 \(d_{SV}=\frac{d^{3}_{V}}{d^2_S}\) \(d_{st}\) \(\mbox{Stokes}\)直径 与颗粒具有相同密度且在同样介质中
具有相同自由沉降速度(层流区)的直径\(d_a\) 投影面直径 与置于稳定颗粒投影面积相同的圆直径 \(A=\frac{\pi}{4}d^2_a\) \(d_L\) 周长直径 与颗粒的投影外形周长相等的圆的直径 \(L=\pi{d_L}\) \(d_A\) 筛分直径 颗粒可以通过的最小方筛孔的宽度
-
-
颗粒群的平均粒度及粒级
-
粒级的表示方法
- 宽\(\Longrightarrow\)窄；
- 上筛孔直径\(d_1\)和下筛孔直径\(d_2\)，用\([d_1, d_2]\)或者\(-d_1+d_2\)；
-
粒群的平均粒度
-
\(d_i\)为各个级别的平均直径，\(\gamma_i\)为各个级别的质量百分率，\(D\)为混合物料的平均直径；
-
计算混合物料平均粒度的方法：
- 算术平均法：\(\frac{\sum_{i=1}^{n}{d_i{\gamma_i}}}{\sum_{i=1}^{n}{\gamma_i}}\)；
- 几何平均法：\({(\prod_{i=1}^{n}{d_i^{r_i})}}^{\frac{1}{\sum_{i=1}^{n}{\gamma_i}}}\)；
- 调和平均法：\(\frac{\sum_{i=1}^{n}{\gamma_i}}{\sum_{i=1}^{n}{\frac{\gamma_i}{d_i}}}\)；
- 算术平均径 \(\gt\) 几何平均径 \(\gt\) 调和平均径；
-
-
-
粒度分布及粒度特性方程
-
粒度分布：颗粒群各粒度区间的颗粒含量占总含量的百分比；
-
粒度组成：将不同粒度由粗到细排列、并指明各个粒级占物料总量的质量百分率；
-
表征粒度分布常用的方法：
-
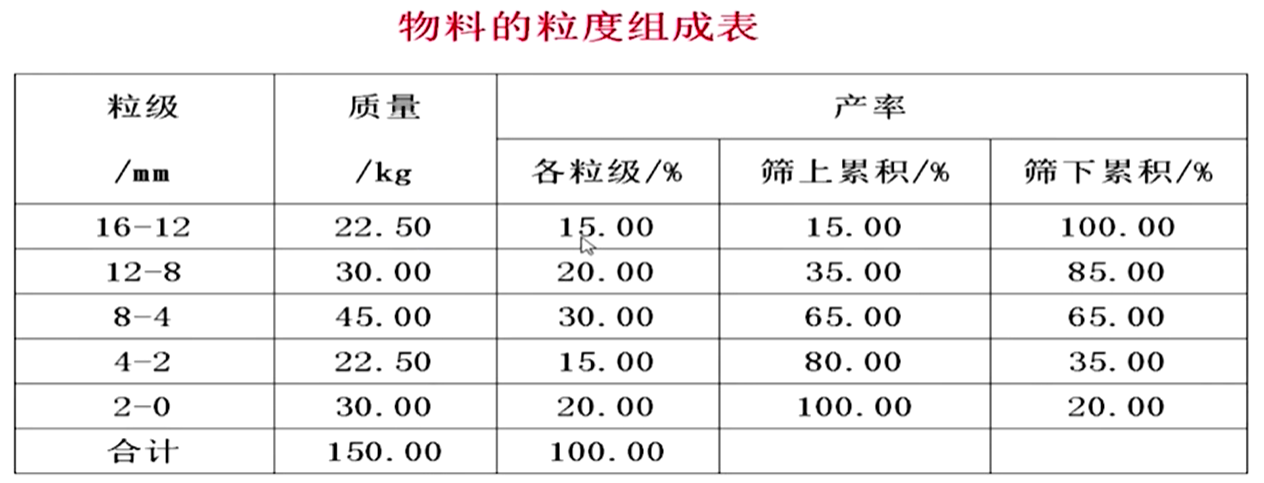
列表法：计算试验后得到原始数据，用表格的形式表达出来；
-
作图法：主要有矩形图、粒度分布图、分布函数图；
-
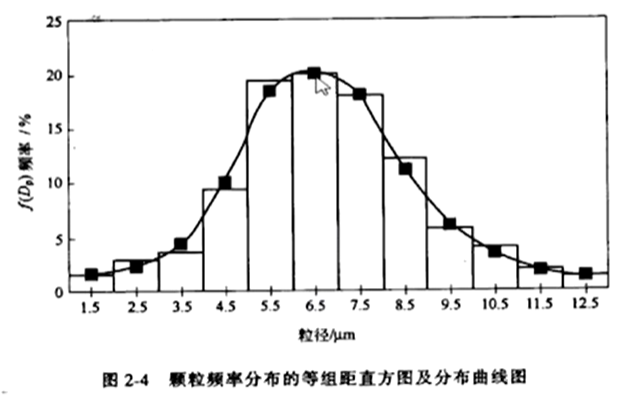
矩形图：把各个直方图回归成一条光滑的曲线，形成颗粒频率分布曲线；
-
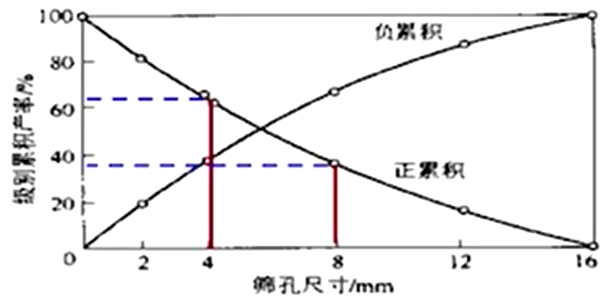
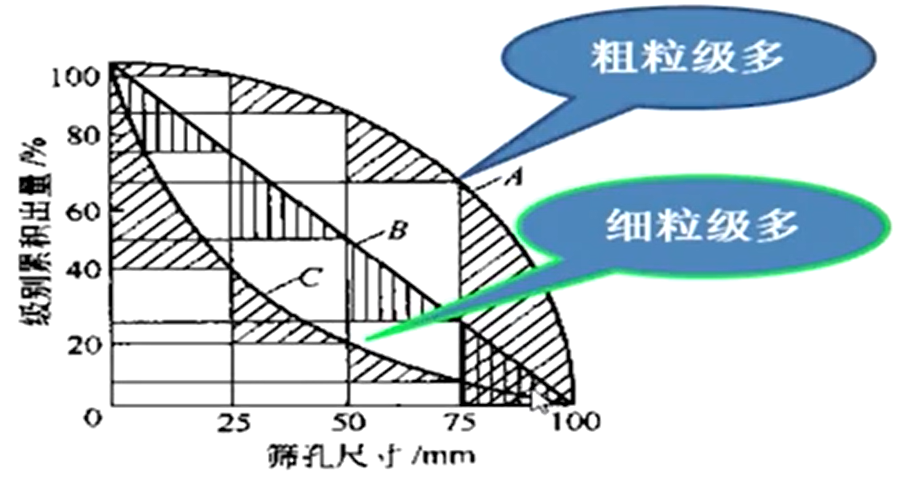
粒度分布图：粒群粒度分布函数图也称为累积粒度特性曲线。曲线横坐标代表粒度，纵坐标代表级别累计产率（包括正负累计：筛上累积为正，筛下累积为负）；
正负累积粒度特性曲线的特点：对称性。
- 可确定任何指定粒度的相应累积产率，或由指定累积产率查得相应粒度；
- 可求出任一粒级(\(d_1\sim d_2\))的产率，它的值等于粒度\(d_1\)与\(d_2\)的纵坐标差值；
- 可由曲线的凹凸形状判断物料的粒度组成情况，凸粗凹细；
构造一个简单的数学模型。
-
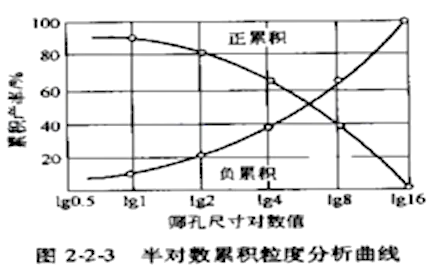
半对数坐标
把横座标取对数后，相邻粒度级之间在横轴上的间距：细粒级增长，粗粒级缩短。
-
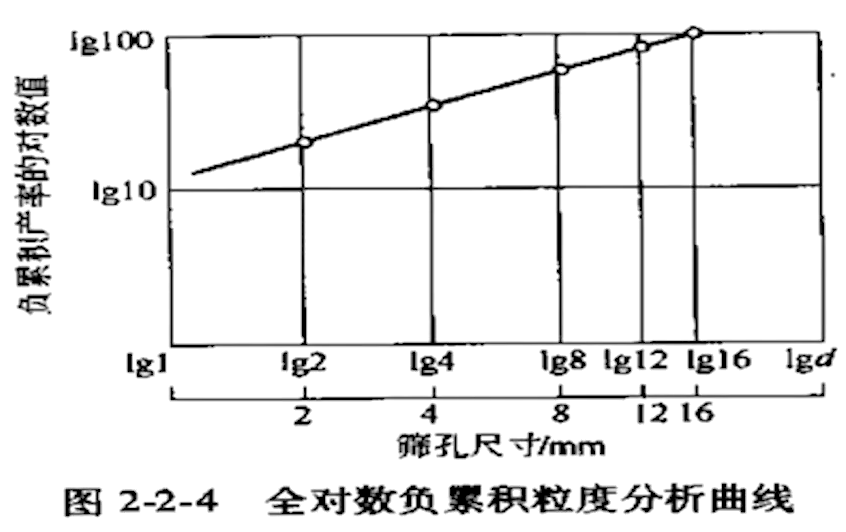
全对数坐标
把产率（纵坐标）也取对数，这样原来的曲线就变成的“直线”，故可建立简单的线性模型，借此确定颗粒粒度在物料中的分布规律。
-
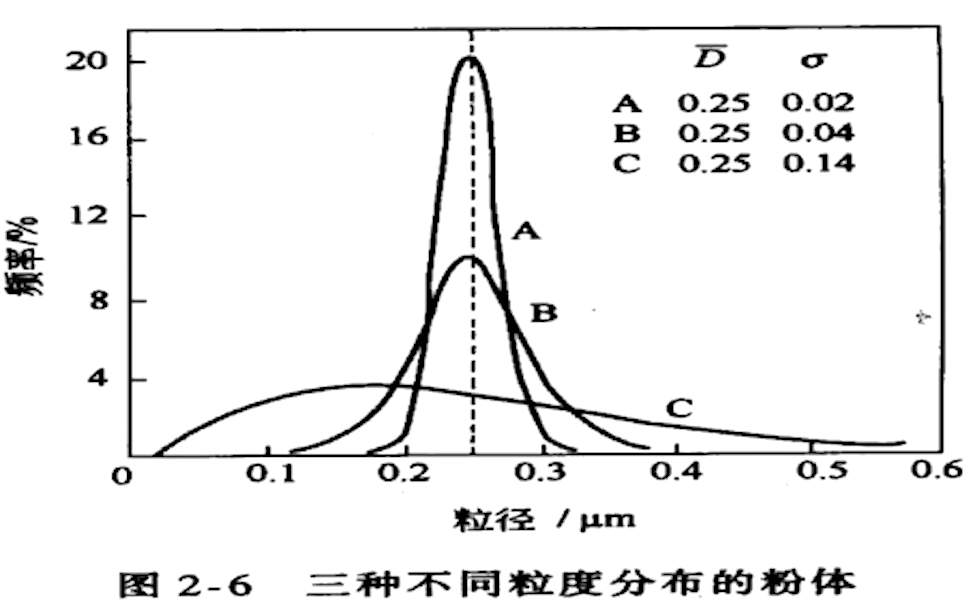
分布函数图
虽然平均粒径\(D_{nL(A)}=D_{nL(B)}=D_{nL(C)}\)，但是分散程度不同\(\sigma_{A}\lt\sigma_B\lt\sigma_C\)；
-
-
函数法：函数法就是用数学方法将物料粒度分析数据归纳、整理，并建立能反映物料粒度分布规律的数学模型—粒度特性方程；
-
高登\(\mbox{Gaudin}\)–安德列耶夫–舒曼\(\mbox{SHuzman}\)公式
\[Y=100\times{(\frac{D}{D_{\max}})}^k \]对一定的物料来说，\(k\)是常数，且一般磨碎产物的\(k\)值常介于0.7$\sim$1.0之间。该公式常用于表达颚式破碎机和圆锥破碎机的破碎产物的粒度特性。
-
罗逊\(\mbox{Rosion}\)—拉姆勒\(\mbox{Rammler}\)公式
\[R=100\times{e^{-bD^n}} \]\(b\)是与产物细度有关的参数，\(n\)是与物料性质相关的参数。适用于破碎的煤、细碎的矿石和磨细的矿料及水泥等。
-
-
-
-
颗粒的几何特性
-
形状系数
- 表面形状系数：\(\Phi_S=\frac{S}{d^2}\)；
- 体积形状系数：\(\Phi_V=\frac{V}{d^3}\)；
- 比表面积形状系数：\(\Phi_{SV}=\frac{\Phi_S}{\Phi_V}\)；
- 比表面积：\(S_V=\frac{S}{V}=\frac{\Phi_S\times{d^2}}{\Phi_V\times{d^3}}=\frac{\Phi_{SV}}{d}\)，所以又有\(\Phi_{SV}=S_Vd\)；
- 球形度：\(\Psi_S=\frac{S_{球}}{S_{粒}}\)，一般来说$\lt\(1，当颗粒为球形时\)=$1；
- 伸长度：\(n=\frac{长径}{短径}=\frac{l}{b}\)；
- 扁平度：\(m=\frac{短径}{厚度}=\frac{b}{h}\)；
-
-
粒度的测量分析方法及选择
-
筛分分析法
网目。
-
水力降尘法
-
显微分析法
-
光散射法
-
电感法
方法 粒度范围
（单位：\(\mathbf{\mu m}\)）测量依据的性质或效应 表达的粒度 直接得到的分布 筛分析
微目筛\(\gt\) 40
5 \(\sim\) 40筛孔 \(d\)筛 质量
体积光学显微镜
电子显微镜
全息照相0.25 \(\sim\) 250
0.01 \(\sim\) 5
2 \(\sim\) 500通常是颗粒投影像的某种尺寸或者某种相当尺寸 \(d_a,d_F,d_{ST}\) 个数 光散射
消光\(X\)光小角散射0.02 \(\sim\) 2000
0.005 \(\sim\) 0.1颗粒对光的散射或消光、颗粒对\(X\)光的散射 同效应的球直径 质量（体积）、个数 重力沉降
离心沉降2 \(\sim\) 100
0.01 \(\sim\) 10悬浮液的浓度、密度或消光等随时间或位置的变化 同沉降速度的球直径，在层流区，即\(d_{st}\) -
-
-
矿物钳布特性及其解离
-
矿石中元素赋存状态
- 富集态独立矿物
- 分散态矿物
-
