2021牛客OI赛前集训营-普及组（第二场）C 题题解

目录

• Description
• Solution
• Code

Description

给你 \(n\) 个点，将其按 \(y_i\) 从大到小排序，从中任意选出一些点，组成序列 \(a\)，要使其满足 $a_{i-2} < a_i < a_{i-1} $ 或 \(a_{i-1} < a_i < a_{i-2}\)，求合法方案数。

Solution

只谈正解。

考虑按照 \(x\) 从小到大排序。

并转化一下思路，从后向前选数，需要保证 \(y\) 是单调递增的。

设 \(f_{i,1/0}\) 表示考虑第 \(i\) 位作为当前序列中 \(y\) 最大的点，\(y\) 第二大的点是从哪转移而来的，\(1\) 表示由右边的点转移而来，\(0\) 表示由左边的点转移而来。

假设当前处理到第 \(i\) 位，前面的已经处理完了，那么对于一位 \(j\)，

配一张图方便理解：

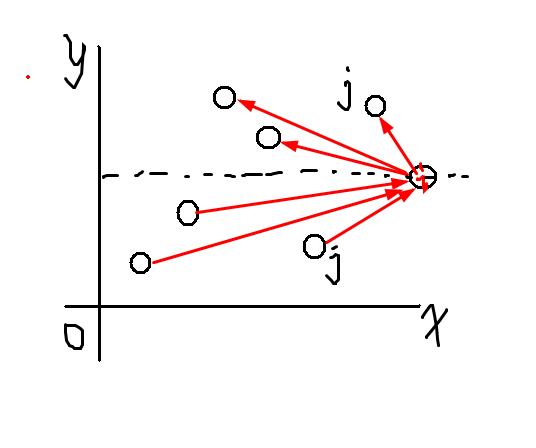
倒序枚举 \(j\)：

• 如果 \(a_{j,y} > a_{i,y}\)，那么 \(f_{j,1} += f_{i,0}\)

此时就是把 \(a_{i,y}\) 当做了 \(y\) 第二大的点，想 \(j\) 这个 \(y\) 值第一大的点转移。

然后你手玩一下题目要求，发现一个合法序列的 \(x\) 一定是一左一右的反复横跳，所以只有 \(f_{i,0}\) 这一个方向可以转移。

• 如果 \(a_{j,y} < a_{i,y}\)，那么 \(f_{i,0} += f_{j,1}\)

这个和上面同理。但还有一个问题，这样 \(f_{i,0}\) 的值不就改变了吗？接下来如果有个位置 \(k\)，满足 \(a_{k,y} > a_{i,y}\) 怎么办？无需多虑，这样做刚好考虑上 \(i\) 作为一个中间点时的情况。

那么为什么不连 \(k\) 以前的也考虑上？这样转移不满足题目要求。

然后这题就做完了，答案是 \(\sum_{i=1}^{n} (f_{i,0} + f_{i,1})\)

挺神奇的考虑方向。

Code

/*
Work by: Suzt_ilymics
Problem: 不知名屑题
Knowledge: 垃圾算法
Time: O(能过)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#define int long long
#define orz cout<<"lkp AK IOI!"<<endl

using namespace std;
const int MAXN = 6000+5;
const int INF = 1e9+7;
const int mod = 1e9+7;

struct node {
    int x, y;
    bool operator < (const node &b) const { return x < b.x; }
}a[MAXN];

int n, ans = 0;
int f[MAXN][2];

int read(){
    int s = 0, f = 0;
    char ch = getchar();
    while(!isdigit(ch))  f |= (ch == '-'), ch = getchar();
    while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
    return f ? -s : s;
}

signed main()
{
	n = read();
	for(int i = 1; i <= n; ++i) a[i].x = read(), a[i].y = read();
	sort(a + 1, a + n + 1);
	for(int i = 1; i <= n; ++i) {
	    f[i][0] = f[i][1] = 1;
	    for(int j = i - 1; j >= 1; --j) {
	        if(a[j].y > a[i].y) f[j][1] = (f[j][1] + f[i][0]) % mod;
	        else f[i][0] = (f[i][0] + f[j][1]) % mod;
        }
    }
    for(int i = 1; i <= n; ++i) {
        ans = (ans + f[i][0] + f[i][1]) % mod;
    }
    printf("%lld\n", (ans - n + mod) % mod);
    return 0;
}