ARC117 VP 记录
A
简单构造。按照 \(1,2,...,A,-1,-2,...,-B\) 的方式构造即可，哪边个数多了就整体合并起来
B
首先排序不会对答案有影响。
发现如果某次操作为 \(x\) ，那么对于 \(\ge x\) 的数之间的差值不会改变，只有 \(< x\) 的最大值和 \(\ge x\) 的最小值之间的差值 \(-1\) 。
那考虑一个两个数之间的差值 \(\Delta = a_i - a_{i-1}\)，那么 \(\Delta\) 可取的数为 \(0 \sim \Delta\) 。
直接乘法原理统计贡献即可。
C
感谢 hyl 和 jjk /qq
很牛逼的构造，想想能不能用四则运算来表示这个转化关系。
转化方法是，把三种颜色分别看成 \(0,1,2\)，然后两个颜色 \(x,y\) 合并就是 \(2(x+y)\bmod 3\) 。
然后考虑一下每个数对顶层的贡献就做完了。
D
首先在草纸上胡乱手模一下。
先考虑链的情况，一定是从一头开始 \(1,2,3...\) 这样填。
考虑在主链上加一个支链，支链第一个数填的一定比主链上的数大，还得多出一个 \(dis\) 的长度，而且填小了一定不合法。下面这个图就十分的生动形象昂
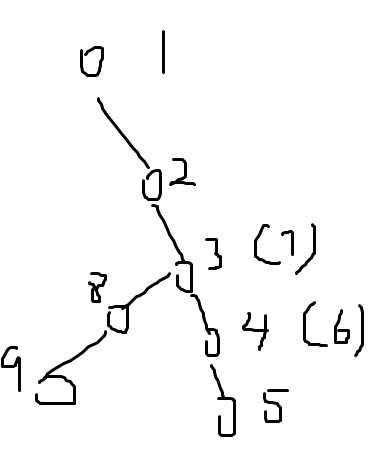
然后你发现它填上的数很像一个 dfs 遍历的形式。
然后你考虑怎样填最优，既然有的点有进有出，有的点可以只进不出，那我们让只进不出的点最多就好了。
那肯定选直径啊。
所以从直径一端开始填，到另一端结束填完就可以了。可以标记一下直径或者长链剖分中的重儿子之类的然后去 dfs。
\(\max \{e_i\}\) 的最小值为 \(2 \times n - \text{直径长度}\) 。
最优性上面已经解释了。
