P2516 [HAOI2010]最长公共子序列 题解
Description
求两个字符串 \(a,b\) 的最长公共子序列以及出现次数。
Solution
看数据范围感觉是个 \(O(nm)\) DP，可是我不会写唉，那先把暴力搞出来吧。
设 \(f_{l,r}\) 表示第一个字符串匹配到 \(l\)，第二个字符串匹配到 \(r\)，并且子序列以 \(a_l,b_r\) 为结尾的最长长度。同时记录一个 \(g_{l,r}\) 表示出现次数。
可以推出一个比较显然的转移方程：
考虑优化，观察这些状态从哪转移的。
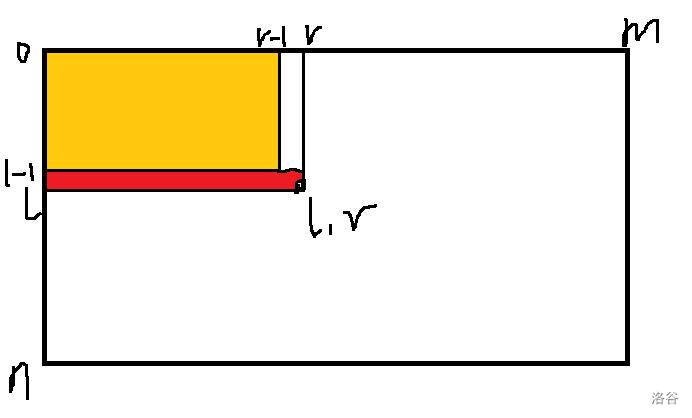
假设我们现在更新 \(f_{l,r}\)。
我们需要知道什么？黄色矩阵中的最大值。
更新 \(g_{l,r}\) 呢，黄色矩阵中所有拥有最大值的 \(f_{i,j}\) 所对应的 \(g_{i,j}\) 的和。
所以我们可以设 \(Max_i = \max_{0\le x<l} \{ f_{x,i}\}, cnt_{i,y} = \sum_{j=0}^{l-1}g_{i,j}(f_{i,j}=y)\)。
因为 \(Max_i\) 和 \(cnt_{i,y}\) 维护的都是 \(0 \sim l-1\) 行的情况，所以我们需要不断更新他们的值。
注意所有的这一行的信息都必须在这一行扫完后再更新。
在递推每一行时，记录一个 nowM 和 sum 分别表示到当前列之前的最大值，和最大值的出现次数。这样就可以把经过的每一列的信息合并在一起，方便更新 \(f_{l,r}\) 的值。
时间复杂度 \(O(n^2)\)。
开这么多二维数组一定会被卡空间。
我们发现 \(g_{l,r}\) 每次只需要存一行留着更新即可，前面的几行都没有用。
然后发现 \(f_{l,r}\) 在状态转移过程中根本没涉及到第一维什么事，直接压掉。
只留下一个二维数组，空间应该够用了。
但是我们发现 \(cnt_{i,y}\) 只会用到它这一列的最大值 \(Max_i\) 所对应的数。那么我们只对 \(cnt_{i,Max_i}\) 维护即可，又压掉一维！
几个注意的点：
- 更新时候的大前提 \(a_l=b_r\) 还是要保留的。
- 但是在记录
nowM和sum时，不管两个字符是否相等都要更新。 - 如果你想给 \(f\) 初始化极小值，那么在 \(f_r < 0\) （压维后） 时就不要更新对应的 \(cnt_r\) 了。
Code
/*
Work by: Suzt_ilymics
Problem: 不知名屑题
Knowledge: 垃圾算法
Time: O(能过)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#define LL long long
#define orz cout<<"lkp AK IOI!"<<endl
using namespace std;
const int MAXN = 1e5+5;
const int INF = 1e9+7;
const int mod = 1e8;
int n, m;
char a[5010], b[5010];
int f[5010], Max[5050], cnt[5050], p[5050];
int read(){
int s = 0, f = 0;
char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'), ch = getchar();
while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
return f ? -s : s;
}
int main()
{
scanf("%s", a + 1); scanf("%s", b + 1);
n = strlen(a + 1), m = strlen(b + 1);
memset(f, 128, sizeof f);
memset(Max, 128, sizeof Max);
f[0] = 0; Max[0] = 0; cnt[0] = 1;
for(int l = 1; l <= n; ++l) {
for(int r = 1, nowM = 0, sum = 0; r <= m; ++r) {
if(nowM < Max[r - 1]) nowM = Max[r - 1], sum = cnt[r - 1];
else if(nowM == Max[r - 1]) sum = (sum + cnt[r - 1]) % mod;
if(a[l] != b[r]) continue;
f[r] = nowM + 1;
p[r] = sum;
}
for(int r = 0; r <= m; ++r) {
if(f[r] < 0) continue;
if(Max[r] < f[r]) Max[r] = f[r], cnt[r] = p[r];
else if(Max[r] == f[r]) cnt[r] = (cnt[r] + p[r]) % mod;
p[r] = 0;
}
}
printf("%d\n%d", f[m] - 1, cnt[m]);
return 0;
}
