图论复习做题记录
前言
不知道为什么就开始刷图论了
获得了许多好的做题经验
最短路
P3096 [USACO13DEC]Vacation Planning G
刷到这题纯粹是因为看lsp做的题看错题号了
Solution:发现 \(n,k\)很小,可以用 SPFA 跑出所有最短路来。所以如果起点是 \(k\) 个点中的一个,可以直接统计答案。如果不是,根据题目描述,每条边必定与一个枢纽相连,所以用邻接表遍历找枢纽即可,找到最短的路径在统计答案,记得判断找不到路径的情况
P3906 Geodetic集合
挺傻逼一题,不知道为什么能评蓝。
Solution:\(n\) 只有 \(40\) !!!一个 Folyd 就完事了。然后判断是否在最短路上也很简单,枚举所有点 \(i\),如果满足 \(dis_{u, i} + dis_{i, v} = dis_{u, v}\) 就是所求点
P2149 [SDOI2009]Elaxia的路线
dis我再不赋初值我就是sb;我再算不对边数就提交我更sb
Solution:
跑四边SPFA,把所有在最短路上的边加入一个新图,标记在两条最短路上都出现过的边,对新图跑拓扑排序,找到最长边就是答案
Hack
Input:
4 4
1 4 2 3
1 2 10
1 3 1
4 2 9
4 3 2
Output:
2
My output:
3
所以虽然能切但是做法是错误的,散了散了
P2176 [USACO11DEC]RoadBlock S / [USACO14FEB]Roadblock G/S
Solution:
发现 \(n, m\) 范围很小啊,一种显然的想法是对没条边都改一次,然后跑最短路找最大增量,但只有 \(90pts\)。
但我们发现一个性质,只有改边最短路上的边才可能对答案有贡献,那就好做了,把最短路上的边都标记然后暴力改边最短路就行了
P2966 [USACO09DEC]Cow Toll Paths G
Solution: \(n \le 250\) + 多组询问 要跑 Floyd 。唯一难处理的是如何在加上点权最大值的条件下取得和的最小值。
题解给出的做法是:将点权从小到大排序,用排序后的点作为 \(k\) 的顺序去更新最短路,这样越到后面更新的就是当前最短路上的最大点权,当然更新的时候 \(i,j,k\) 的点权要取 \(\max\)(因为中间点不一定比起点大)
拓扑排序
P2017 [USACO09DEC]Dizzy Cows G
Solution:没有判断有无解的情况,姑且认为全部有解。先只考虑有向图,对有向图进行拓扑序(队列/DFS),然后对于所有无向边拓扑序大的点连向拓扑序小的点即可
CF1385E Directing Edges
Solution:需要判断无解的情况,这里给出一种方法(只会一种)
将没有入度的点加入队列,然后拓扑排序。如果遍历到的点的数量 \(< n\),就是无解
P2505 [HAOI2012]道路
Description \(\&\) 双倍经验
考虑让分别让每个点作为源点
用在最短路上的边重建图,得到一个 DAG,我们称之最短路图。
然后在这个 DAG 上跑拓扑可以得到 \(S\) 到某个结点 \(u\) 的路径条数 \(cnt1_u\)。
把这个 DAG 建反边,再跑一遍拓扑,可以得到 \(u\) 到终点的条数 \(cnt2_u\)
那么对于所有在图上的边,对它的贡献为 \(cnt1_u \times cnt2_v\)。
注意反向 DAG 的初始化
/*
Work by: Suzt_ilymics
Problem: 不知名屑题
Knowledge: 垃圾算法
Time: O(能过)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#define int long long
#define LL long long
#define orz cout<<"lkp AK IOI!"<<endl
using namespace std;
const int MAXN = 5000+5;
const int INF = 1e9+7;
const int mod = 1e9+7;
struct edge {
int from, to, w, nxt;
}e[MAXN << 1];
int head[MAXN], num_edge = 1;
struct Edge {
int to, nxt;
}e1[MAXN << 1], e2[MAXN << 1];
int head1[MAXN], num_edge1 = 1;
int head2[MAXN], num_edge2 = 1;
int n, m;
int dis[MAXN], cnt1[MAXN], cnt2[MAXN];
int id[MAXN], Id[MAXN], ans[MAXN];
bool vis[MAXN];
int read(){
int s = 0, f = 0;
char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'), ch = getchar();
while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
return f ? -s : s;
}
void add_edge(int from, int to, int w) { e[++num_edge] = (edge){from, to, w, head[from]}, head[from] = num_edge; }
void add_edge1(int from, int to) { e1[++num_edge1] = (Edge){to, head1[from]}, head1[from] = num_edge1; }
void add_edge2(int from, int to) { e2[++num_edge2] = (Edge){to, head2[from]}, head2[from] = num_edge2; }
void SPFA(int s) {
memset(dis, 0x3f, sizeof dis);
memset(vis, 0x3f, sizeof vis);
queue<int> q;
q.push(s), dis[s] = 0, vis[s] = true;
while(!q.empty()) {
int u = q.front(); q.pop();
vis[u] = false;
for(int i = head[u]; i; i = e[i].nxt) {
int v = e[i].to;
if(dis[v] > dis[u] + e[i].w) {
dis[v] = dis[u] + e[i].w;
if(!vis[v]) q.push(v), vis[v] = true;
}
}
}
}
void Topsort1(int s) {
queue<int> q;
q.push(s);
cnt1[s] = 1;
while(!q.empty()) {
int u = q.front(); q.pop();
for(int i = head1[u]; i; i = e1[i].nxt) {
int v = e1[i].to;
cnt1[v] += cnt1[u];
id[v] --;
if(!id[v]) q.push(v);
}
}
}
void Topsort2() {
queue<int> q;
for(int i = 1; i <= n; ++i) cnt2[i] = 1;
for(int i = 1; i <= n; ++i) if(!Id[i]) q.push(i);
while(!q.empty()) {
int u = q.front(); q.pop();
for(int i = head2[u]; i; i = e2[i].nxt) {
int v = e2[i].to;
cnt2[v] += cnt2[u];
Id[v] --;
if(!Id[v]) q.push(v);
}
}
}
signed main()
{
n = read(), m = read();
for(int i = 1, u, v, w; i <= m; ++i) {
u = read(), v = read(), w = read();
add_edge(u, v, w);
}
for(int i = 1; i <= n; ++i) {
SPFA(i);
memset(id, false, sizeof id);
memset(Id, false, sizeof Id);
memset(head1, false, sizeof head1);
memset(head2, false, sizeof head2);
memset(cnt1, false, sizeof cnt1);
memset(cnt2, false, sizeof cnt2);
num_edge1 = num_edge2 = 1;
for(int j = 2; j <= num_edge; ++j) {
if(dis[e[j].from] + e[j].w == dis[e[j].to]) {
add_edge1(e[j].from, e[j].to);
add_edge2(e[j].to, e[j].from);
id[e[j].to]++, Id[e[j].from]++;
}
}
Topsort1(i);
Topsort2();
for(int j = 2; j <= num_edge; ++j) {
if(dis[e[j].from] + e[j].w == dis[e[j].to]) {
ans[j] = (ans[j] + cnt1[e[j].from] * cnt2[e[j].to] % mod) % mod;
}
}
}
for(int i = 2; i <= num_edge; ++i) printf("%lld\n", ans[i]);
return 0;
}
网络流
P6268 [SHOI2002]舞会
Solution:二分图匹配问题,网络流跑的飞快
因为 二分图最大独立集等于 \(n -\) 最小点覆盖 \(=\) \(n -\) 二分图最大匹配数
又因为题目中并没有给出那个是男的那个是女的 安能辨我是雄雌?
所以对其进行染色 钦定谁男谁女
然后就变成一个网络流跑二分图的板子了
P1361 小M的作物
Solution:
很妙的网络流最小割问题。
显然要把所有种子分成两部分,所以考虑最小割。
源点和汇点分别为两块田 \(A,B\)。
源点向所有种子连边,流量为 \(a_i\);所有种子向汇点连边,流量为 \(b_i\)。
这样跑最大流后,两条边只会有一条被留下,另一条边相当于割掉了,符合题意。
考虑集合如何处理,用类似的思想
对于每个集合建两个虚点,源点向一个虚点连边,流量为 \(c_1\);另一个虚点向汇点连边,流量为 \(c_2\)。
第一个虚点向集合中的所有点连边,流量为正无穷,集合中的所有点向另一个虚点连边,流量为正无穷。
集合断边说明选择了另一边(当然都断就都不选)
假设出现下面的情况
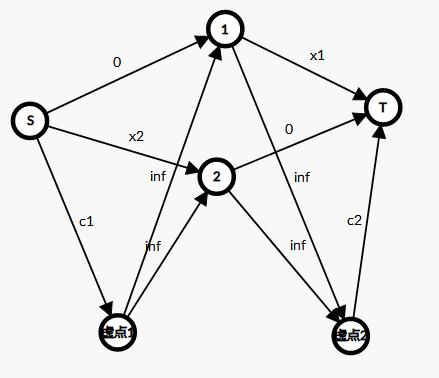
显然还有两条边没有流完,而这个图最后的情况一定是左边或者右边全没有流量(即把边割完了),或者两个虚点的流量都流完了(即都不选的情况)
一类最大权闭合子图问题
其实是三倍经验
大体意思一般为:想要使某个事件发生必须使它发生的条件发生
更通俗的说:你想要的用某个东西的获得收益,必须先有这个东西,而这个东西是由其他零件组装而成,为了得到这些零件你需要付出一定的代价。求最大总收益,总收益 = 每个收益 - 所付出的代价。
建图方式:
源点向每个付出代价的零件连边,流量为代价
每个零件向它能组成的成品连边,流量为正无穷
每个成品向汇点连边,流量为收益。
(或者把整个过程反过来)
如何出选择的方案?
把上面那个建图方式反过来。
最后一次 bfs 然后输出每个 dis[i] != -1 的点
正确性?
每个 dis[i] != -1 的点都代表被选了,那么他们对应的零件也应被选
没有找到严谨的证明,大概这种二分图形式的边只会 bfs 一次,所以最后 dis[i] != -1 的点一定为选择的?
P4177 [CEOI2008]order
Solution:
模型与上面的相似,但解法略有不同
思考建图时的主要问题是:暂时租用和永久购买,只要满足一个就可以。
这种题的思路是将两种边连到同一个路径上,这样割边的时候只会割断其中一根,满足了只需满足一个的条件。
建图方法:源点向每个机器连永久购买的边,每个机器向所需要它的任务连暂时购买的边,每个任务向汇点连它的价值。
跑最小割即可。
强联通分量
P4819 [中山市选]杀人游戏
很容易想到,把图缩点后那些入度为 \(0\) 的点是警察必须要问的点
考虑一种特殊情况:
几个入度为 \(0\) 的点,还剩下最后一个没问且整个图中其他点都不是杀手,那么最后一个就不需要问了。
现在需要特判这种情况:
当这个点能到达的所有点都能被其他入度为 \(0\) 的点到达时,他就是这个特殊点。
注意重建图时判断重边,这里给出两种方法:
- map 映射
- 每次只处理一个点的情况,具体看代码
for(int i = 1; i <= n; ++i) { // 一种比较好的防止重边的方法,复杂度 O(2m)
for(int j = head[i]; j; j = e[j].nxt) {
int v = e[j].to;
if(num[i] == num[v] || vis[num[v]]) continue;
Add_edge(num[i], num[v]);
id[num[v]]++;
vis[num[v]] = true;
}
for(int j = head[i]; j; j = e[j].nxt) vis[num[e[j].to]] = false;
}
P2403 [SDOI2010]所驼门王的宝藏
图不太好建啊。如何减少建边才是关键。
把每一行看做一个虚点,每一列看做一个虚点。
每个横天门向这一行的虚点建边,每个纵寰门向这一列的虚点建边。
每个任意门向周围的宝藏房间建边。(暴力枚举周围三行的宝藏房间建边即可)
每一行的虚点向这一行所有宝藏房间连边,
每一列的虚点向这一列所有宝藏房间连边。
然后 tarjan 缩点,在 DAG 上找个最长路就做完了
温馨提示:内存卡的很紧


 浙公网安备 33010602011771号
浙公网安备 33010602011771号