一些有趣的线段树玩法

目录

• 写在前面
• CF803G Periodic RMQ Problem
• CF915E Physical Education Lessons
• P6327 区间加区间sin和
• CF242E XOR on Segment
• CF438D The Child and Sequence
• CF703D Mishka and Interesting sum
• P4211 [LNOI2014]LCA
• CF920F SUM and REPLACE

写在前面

想必大家都有了一定的线段树基础，所以来做点更有意思的线段树吧（

转存的 Limit の线段树题单

CF803G Periodic RMQ Problem

先来道黑题热热身

Description

题面：CF803G Periodic RMQ Problem

给你一个序列 \(a\) 让你支持: 区间赋值;询问区间最小值
我们觉得这个问题太水了,所以我们不会给你序列 \(a\)
而是给你序列一个长度为 \(n\) 的序列 \(b\) ,把 \(b\) 复制粘贴 \(k\) 次就可以得到 \(a\)。
数据范围：\(n \le 10^5,k \le 10^4,q \le 10^5,b_i \le 10^9, 1 \le l \le r \le n \times k\)

Solution

维护的线段树操作不难，麻烦的地方在于对原序列的处理，理解思想后完全可以自己yy出代码。

看到 “区间覆盖，区间最小值” ，这不板子？
但是，序列长度可是 \(n \times k = 10^9\) 啊。

发现询问涉及到的点只有 \(10^5\) 级别，考虑进行离散化处理，只保留对答案有贡献的信息。

注意：对答案有贡献的信息不仅仅是询问涉及到的点，还有相邻的两个涉及到的点的区间也对答案有贡献
（因为这个区间内的最小值可能比两个端点更小）。

蓝色箭头是询问涉及过的点，相邻的两个涉及过的点的区间被压缩成一个点来处理（如果相邻两个涉及过的点之间没有区间就不压缩）。

把这两种点都放进一个新的序列（红色序列），然后在新的序列上进行修改查询操作即可。
注意映射好询问涉及到的点在红色序列中的位置。

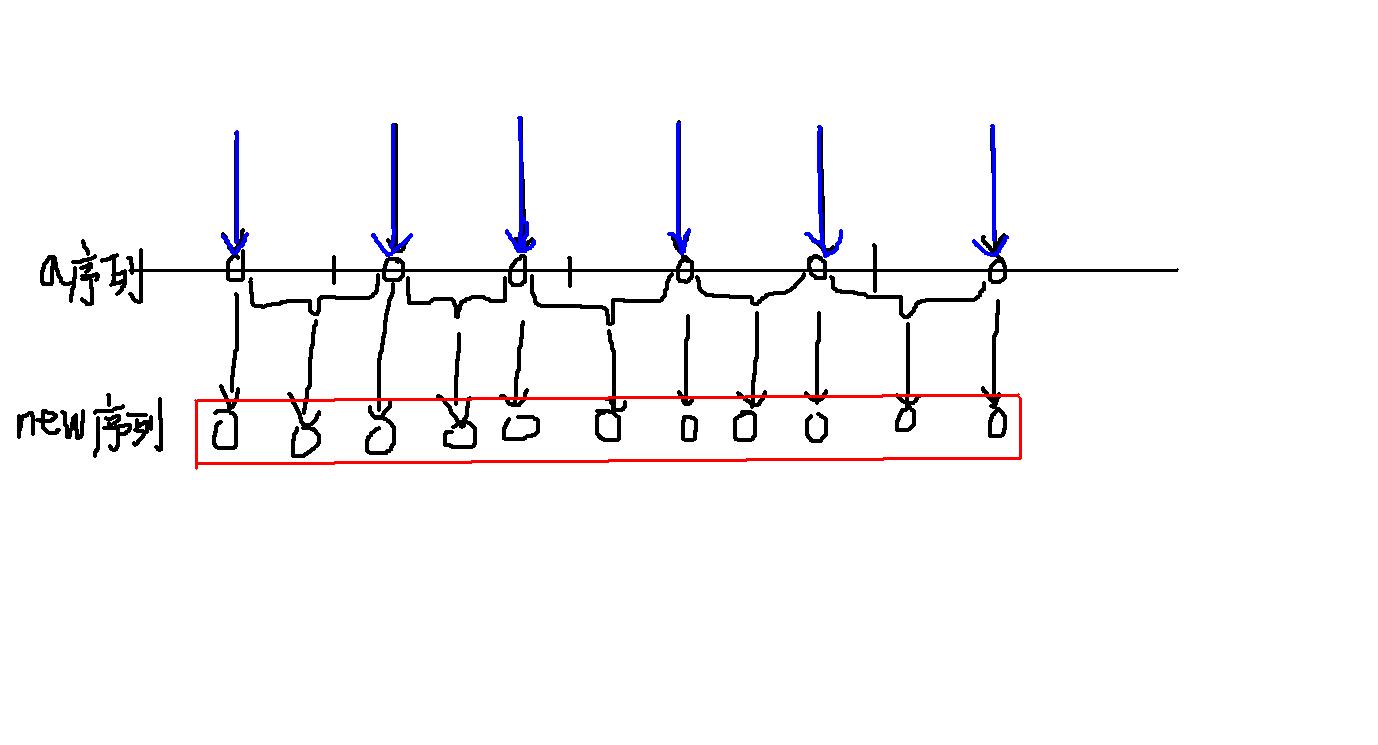
图床崩了，原图丢失，有时间在画一个

注意将区间压缩成一个点时的处理：

• 如果区间长度超过 \(n\)，直接加入原来整段区间的最小值（但是数据没卡这个地方）
• 如果在同一个区间内，加入这个区间内的最小值
• 如果跨越了两个区间，加入区间 \([1, r]\) 和 \([l, n]\) 的最小值

这种做法在复杂度和空间消耗上都比较优秀。

剩下的看代码吧，重要步骤都有注释，如果有不懂的也可以在评论区提出

Code

/*
Work by: Suzt_ilymics
Knowledge: ??
Time: O(??)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define LL long long
#define orz cout<<"lkp AK IOI!"<<endl

using namespace std;
const int MAXN = 2e5+5; // 注意开的数组大小（自己算算应该用多少 
const int INF = 1e9+7;
const int mod = 1e9+7;

struct Ques{
    int opt, l, r, val;
}q[MAXN];

int n, K, m;
int a[MAXN], b[MAXN << 1], Cnt = 0, pre[MAXN << 1];
int date[MAXN], cnt = 0, date_num = 0;

int read(){
    int s = 0, f = 0;
    char ch = getchar();
    while(!isdigit(ch))  f |= (ch == '-'), ch = getchar();
    while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
    return f ? -s : s;
}

struct Big_Seg{ // 采用结构体，码量会更少哦 
    #define lson i << 1
    #define rson i << 1 | 1
    struct Tree{
        int min, lazy;
    }tree[MAXN << 3];
    void Push_up(int i) { tree[i].min = min(tree[lson].min, tree[rson].min); }
    void Push_down(int i) {
        if(tree[i].lazy) {
            tree[lson].lazy = tree[rson].lazy = tree[i].lazy;
            tree[lson].min = tree[rson].min = tree[i].lazy;
            tree[i].lazy = 0;
        }
    }
    void Build(int i, int l, int r) { //两个建树分别给两个线段树用 
        if(l == r) { tree[i].min = b[l]; return ; }
        int mid = (l + r) >> 1;
        Build(lson, l, mid), Build(rson, mid + 1, r);
        Push_up(i);
    }
    void Build0(int i, int l, int r) {
        if(l == r) { tree[i].min = a[l]; return ; }
        int mid = (l + r) >> 1;
        Build0(lson, l, mid), Build0(rson, mid + 1, r);
        Push_up(i);
    }
    void Change(int i, int l, int r, int L, int R, int k) {
        if(L <= l && r <= R) {
            tree[i].min = tree[i].lazy = k;
            return ;
        }
        Push_down(i);
        int mid = (l + r) >> 1;
        if(mid >= L) Change(lson, l, mid, L, R, k);
        if(mid < R) Change(rson, mid + 1, r, L, R, k);
        Push_up(i);
    }
    int Get_min(int i, int l, int r, int L, int R) {
        if(L <= l && r <= R) return tree[i].min;
        Push_down(i);
        int mid = (l + r) >> 1, ans = INF;
        if(mid >= L) ans = min(ans, Get_min(lson, l, mid, L, R));
        if(mid < R) ans = min(ans, Get_min(rson, mid + 1, r, L, R));
        return ans;
    }
}Seg[2];

int main()
{
    n = read(), K = read();
    for(int i = 1; i <= n; ++i) a[i] = read();
    Seg[0].Build0(1, 1, n); // 先对给定的小序列建树 
    m = read();
    for(int i = 1; i <= m; ++i) {
        q[i].opt = read(), q[i].l = read(), q[i].r = read();
        date[++ cnt] = q[i].l, date[++ cnt] = q[i].r;
        if(q[i].opt == 1) q[i].val = read();
    }
    sort(date + 1, date + cnt + 1); date[0] = -INF;
    for(int i = 1; i <= cnt; ++i) if(date[i] != date[i - 1]) date[++ date_num] = date[i]; // 离散化 
    
    //一下是构造新序列b过程（即图中的红色序列 
    for(int i = 1; i < date_num; ++i) {
        if(date[i] % n == 0) b[++Cnt] = a[n];
        else b[++Cnt] = a[date[i] % n];
        pre[i] = Cnt; // 进行第二次映射的处理 
        if(date[i + 1] > date[i] + 1){
            if((date[i + 1] - 1) - (date[i] + 1) >= n) { // 压缩区间长度超过 n 时 
                b[++Cnt] = Seg[0].tree[1].min;
                continue;
            }
            int l = (date[i] + 1) % n, r = (date[i + 1] - 1) % n; //映射到复制前的序列中的位置 
            if(l == 0) l = n;
            if(r == 0) r = n;
            if(l <= r) b[++Cnt] = Seg[0].Get_min(1, 1, n, l, r); // 在一个区间内 
            else b[++Cnt] = min(Seg[0].Get_min(1, 1, n, 1, r), Seg[0].Get_min(1, 1, n, l, n)); // 不在一个区间内，用两段区间合并 
        }
    }
    if(date[date_num] % n == 0) b[++Cnt] = a[n];
    else b[++Cnt] = a[date[date_num] % n];
    pre[date_num] = Cnt;
    
    for(int i = 1; i <= m; ++i) { 
        q[i].l = lower_bound(date + 1, date + date_num + 1, q[i].l) - date; // 询问的点向离散化后映射 
        q[i].r = lower_bound(date + 1, date + date_num + 1, q[i].r) - date;
        q[i].l = pre[q[i].l], q[i].r = pre[q[i].r]; // 向b序列中的映射 
    }
    Seg[1].Build(1, 1, Cnt); //对 b序列建树 
    for(int i = 1; i <= m; ++i) { //直接修改+查询即可 
        if(q[i].opt == 1) Seg[1].Change(1, 1, Cnt, q[i].l, q[i].r, q[i].val);
        else printf("%d\n", Seg[1].Get_min(1, 1, Cnt, q[i].l, q[i].r));
    }
    return 0;
}

总结

对于所维护的区间过大时，考虑离散化只留下有用的信息来达到节约空间的目的。

CF915E Physical Education Lessons

Description

题面：CF915E Physical Education Lessons

一个长度为 \(1e9\) 的 \(01\) 序列，开始都是1，要求支持区间修改 \(0/1\) ,每次修改后都要输出整个序列中 \(1\) 的个数

Solution

\(1e9\) 开不下啊，考虑动态开点线段树

维护操作时和线段树类似，用到哪块区间就新建哪块区间（例如询问时和下放懒标记时）

Code

/*
Work by: Suzt_ilymics
Knowledge: 动态开点线段树 
Time: O(能过)
当线段树维护的范围到达1e9
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define LL long long
#define orz cout<<"lkp AK IOI!"<<endl

using namespace std;
const int MAXN = 15001000;
const int INF = 1e9+7;
const int mod = 1e9+7;

int n, m;

int read(){
    int s = 0, f = 0;
    char ch = getchar();
    while(!isdigit(ch))  f |= (ch == '-'), ch = getchar();
    while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
    return f ? -s : s;
}

namespace CMT{
    int root, node_num = 0, sum[MAXN], lazy[MAXN], lson[MAXN], rson[MAXN];
    void Push_up(int i) { sum[i] = sum[lson[i]] + sum[rson[i]]; }
    void Push_down(int i, int l, int r) { // 一次只需要开两个点，剩下的点用到的时候在开，节省空间 
        if(lazy[i] == -1) return ;
        int mid = (l + r) >> 1; // 确定序列的长度 
        if(!lson[i]) lson[i] = ++ node_num; // 没有的话就开一个点 
        if(!rson[i]) rson[i] = ++ node_num;
        sum[lson[i]] = lazy[i] * (mid - l + 1), lazy[lson[i]] = lazy[i];
        sum[rson[i]] = lazy[i] * (r - mid), lazy[rson[i]] = lazy[i];
        lazy[i] = -1;
    }
    void Change(int &now_, int l, int r, int L, int R, int val) {
        if(!now_) now_ = ++ node_num; // 如果没有这个结点，新建这个结点 
        if(L <= l && r <= R) {
            sum[now_] = (r - l + 1) * val; // 
            lazy[now_] = val; 
            return ;
        }
        Push_down(now_, l, r); // 如果需要更精确的序列，就下放新建结点 
        int mid = (l + r) >> 1;
        if(mid >= L) Change(lson[now_], l, mid, L, R, val);
        if(mid < R) Change(rson[now_], mid + 1, r, L, R, val);
        Push_up(now_);
    }
}
using namespace CMT;

int main()
{
    n = read(), m = read();
    memset(lazy, -1, sizeof lazy);
    Change(root, 1, n, 1, n, 0); // 用0表示有工作日，1表示非工作日 
    for(int i = 1, l, r, k; i <= m; ++i) {
        l = read(), r = read(), k = read();
        Change(root, 1, n, l, r, 2 - k);
        printf("%d\n", n - sum[1]);
    }
    return 0;
}

P6327 区间加区间sin和

Description

P6327 区间加区间sin和

Solution

根据三角恒等变换公式，有

\[\sin (a+b) = \sin a \cos b + \cos a \sin b \]

\[\cos (a+b) = \cos a \cos b - \sin a \sin b \]

主要是要证明 \(\sin\) 能够满足区间加的性质

证明如下：

设有两个角 \(a, b\)，新加的值为 \(k\)， 则

\[\sin (a+k) + \sin (b+k) = (\sin a + \sin b) \cos k + (\cos a + \cos b) \sin k \]

将上面的公式代入化简即可，同时发现 \(\cos\) 也能化成类似的形式

\[\cos (a+k) + \cos (b+k) = (\cos a + \cos b) \cos k - (\sin a + \sin b) \sin k \]

那么一切就好做了，按照上面两个结论修改即可

Code

/*
Work by: Suzt_ilymics
Knowledge: ??
Time: O(??)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define LL long long
#define int long long
#define orz cout<<"lkp AK IOI!"<<endl

using namespace std;
const int MAXN = 2e5+5;
const int INF = 1e9+7;
const int mod = 1e9+7;

int n, m;
int a[MAXN];

int read(){
    int s = 0, f = 0;
    char ch = getchar();
    while(!isdigit(ch))  f |= (ch == '-'), ch = getchar();
    while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
    return f ? -s : s;
}

namespace Seg{
    #define lson i << 1
    #define rson i << 1 | 1
    struct Tree{
        double Sin, Cos; int lazy;
    }tree[MAXN << 2];
    void Push_up(int i) {
        tree[i].Sin = tree[lson].Sin + tree[rson].Sin;
        tree[i].Cos = tree[lson].Cos + tree[rson].Cos;
    }
    void Build(int i, int l, int r) {
        if(l == r) {
            tree[i].Sin = sin(a[l]);
            tree[i].Cos = cos(a[l]);
            return ;
        }
        int mid = (l + r) >> 1;
        Build(lson, l, mid), Build(rson, mid + 1, r);
        Push_up(i);
    }
    void Push_down(int i) {
        if(tree[i].lazy) {
            tree[lson].lazy += tree[i].lazy;
            tree[rson].lazy += tree[i].lazy;
            double Sin_lson = tree[lson].Sin, Sin_rson = tree[rson].Sin;
            int tag = tree[i].lazy;
            tree[lson].Sin = Sin_lson * cos(tag) + tree[lson].Cos * sin(tag);
            tree[lson].Cos = tree[lson].Cos * cos(tag) - Sin_lson * sin(tag);
            tree[rson].Sin = Sin_rson * cos(tag) + tree[rson].Cos * sin(tag);
            tree[rson].Cos = tree[rson].Cos * cos(tag) - Sin_rson * sin(tag);
            tree[i].lazy = 0;
        }
    }
    void Add(int i, int l, int r, int L, int R, int val) {
        if(L <= l && r <= R) {
            double Sin = tree[i].Sin;
            tree[i].Sin = tree[i].Sin * cos(val) + tree[i].Cos * sin(val);
            tree[i].Cos = tree[i].Cos * cos(val) - Sin * sin(val);
            tree[i].lazy += val; 
            return ;
        }
        Push_down(i);
        int mid = (l + r) >> 1;
        if(mid >= L) Add(lson, l, mid, L, R, val);
        if(mid < R) Add(rson, mid + 1, r, L, R, val);
        Push_up(i);
    }
    double Get_Sin(int i, int l, int r, int L, int R) {
        if(L <= l && r <= R) return tree[i].Sin;
        Push_down(i);
        int mid = (l + r) >> 1; double ans = 0;
        if(mid >= L) ans += Get_Sin(lson, l, mid, L, R);
        if(mid < R) ans += Get_Sin(rson, mid + 1, r, L, R);
        return ans;
    }
}

signed main()
{
    n = read();
    for(int i = 1; i <= n; ++i) a[i] = read();
    Seg::Build(1, 1, n);
    m = read();
    for(int i = 1, opt, l, r, val; i <= m; ++i) {
        opt = read(), l = read(), r = read();
        if(opt == 1) {
            val = read();
            Seg::Add(1, 1, n, l, r, val);
        } else {
            double Ans = Seg::Get_Sin(1, 1, n, l, r);
            printf("%.1f\n", Ans);
        }
    }
    return 0;
}

CF242E XOR on Segment

Description

CF242E XOR on Segment

Solution

手膜一下发现，当区间和加起来时不能直接进行区间异或，因为不能满足类似于上面那个题的性质

这里我们考虑使用拆位线段树

将每一个数进行二进制拆分，对每个二进制位分别建树

又因为 1^1=0, 0^1=1 和 1^0=1, 0^0=0

即，异或 \(1\) 时进行取反，否则不变

所以区间异或时取出每一位，是 \(1\) 就进行修改，否则无需修改，修改操作也十分类似于区间翻转

Code

/*
Work by: Suzt_ilymics
Knowledge: ??
Time: O(??)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define LL long long
#define int long long
#define orz cout<<"lkp AK IOI!"<<endl

using namespace std;
const int MAXN = 1e5+5;
const int INF = 1e9+7;
const int mod = 1e9+7;

int n, m, ans;
int a[21][MAXN];

int read(){
    int s = 0, f = 0;
    char ch = getchar();
    while(!isdigit(ch))  f |= (ch == '-'), ch = getchar();
    while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
    return f ? -s : s;
}

struct SEG{
    #define lson i << 1
    #define rson i << 1 | 1
    struct Tree{
        int sum, lazy, len;
    }tree[MAXN << 2];
    void Push_up(int i) { tree[i].sum = tree[lson].sum + tree[rson].sum; }
    void Build(int i, int l, int r, int rk) {
        tree[i].len = r - l + 1;
        if(l == r) {
            tree[i].sum = a[rk][l]; return ;
        }
        int mid = (l + r) >> 1;
        Build(lson, l, mid, rk), Build(rson, mid + 1, r, rk);
        Push_up(i);
    }
    void Push_down(int i) {
        if(tree[i].lazy) {
            tree[lson].lazy ^= 1, tree[rson].lazy ^= 1;
            tree[lson].sum = tree[lson].len - tree[lson].sum;
            tree[rson].sum = tree[rson].len - tree[rson].sum;
            tree[i].lazy = 0;
        }
    }
    void Xor(int i, int l, int r, int L, int R, int val) {
        if(L <= l && r <= R) {
            tree[i].sum = tree[i].len - tree[i].sum;
            tree[i].lazy ^= val; 
            return ;
        }
        Push_down(i);
        int mid = (l + r) >> 1;
        if(mid >= L) Xor(lson, l, mid, L, R, val);
        if(mid < R) Xor(rson, mid + 1, r, L, R, val);
        Push_up(i);
    }
    int Get_sum(int i, int l, int r, int L, int R) {
        if(L <= l && r <= R) return tree[i].sum;
        Push_down(i);
        int mid = (l + r) >> 1, ans = 0;
        if(mid >= L) ans += Get_sum(lson, l, mid, L, R);
        if(mid < R) ans += Get_sum(rson, mid + 1, r, L, R);
        return ans;
    }
}Seg[21];

signed main()
{
    n = read();
    for(int i = 1, x; i <= n; ++i) {
        x = read();
        for(int j = 0; j <= 20; ++j) a[j][i] = ((x >> j) & 1);
    }
    for(int i = 0; i <= 20; ++i) Seg[i].Build(1, 1, n, i);
    m = read();
    for(int i = 1, opt, l, r, x; i <= m; ++i) {
        opt = read(), l = read(), r = read();
        if(opt == 1) {
            ans = 0;
            for(int j = 0; j <= 20; ++j) ans += (1 << j) * Seg[j].Get_sum(1, 1, n, l, r);
            printf("%lld\n", ans);
        } else  {
            x = read();
            for(int j = 0; j <= 20; ++j) {
                if((x >> j) & 1) Seg[j].Xor(1, 1, n, l, r, 1);
            }
        }
    }
    return 0;
}

CF438D The Child and Sequence

Description

CF438D The Child and Sequence

Solution

特点在于区间取模

其实和 花神游历各国 和 GSS4 的思路类似

可以证明：如果模数 \(m \le x\)，则 \(x \mod m < \frac{x}{2}\)

那么最多只会模 \(\log x\) 次，和区间开方一样的处理方式即可（维护一个区间最值，暴力开方）

证明：

• 如果 \(m > x\), 那么 \(x \mod m = x\)

• 如果 \(m < x\)，考虑如何让 \(x\) 剩下的值最大？一个显然的想法是模数 \(m\) 尽可能大
  如果 \(m > \frac{x}{2}\) ，那么剩下的一定小于 \(\frac{x}{2}\)，如果 \(m < \frac{x}{2}\)，那么更不必说了，所以当 \(m = \frac{x}{2}\) 时，\(x\) 剩下的值最大，所以 \(x\) 最多进行取模 \(\log x\) 次

代码的话，应该和区间开方差不多吧

Code

/*
Work by: Suzt_ilymics
Knowledge: ??
Time: O(??)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define LL long long
#define int long long
#define orz cout<<"lkp AK IOI!"<<endl

using namespace std;
const int MAXN = 1e5+5;
const int INF = 1e9+7;
const int mod = 1e9+7;

int n, m;
int a[MAXN];

int read(){
    int s = 0, f = 0;
    char ch = getchar();
    while(!isdigit(ch))  f |= (ch == '-'), ch = getchar();
    while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
    return f ? -s : s;
}

namespace Seg{
    #define lson i << 1
    #define rson i << 1 | 1
    struct Tree{
        int sum, max;
    }tree[MAXN << 2];
    void Push_up(int i) {
        tree[i].sum = tree[lson].sum + tree[rson].sum;
        tree[i].max = max(tree[lson].max, tree[rson].max);
    }
    void Build(int i, int l, int r) {
        if(l == r) {
            tree[i].max = tree[i].sum = a[l]; 
            return ;
        }
        int mid = (l + r) >> 1;
        Build(lson, l, mid), Build(rson, mid + 1, r);
        Push_up(i);
    }
    void Change(int i, int l, int r, int L, int R, int k) {
        if(L <= l && r <= R) {
            tree[i].max = tree[i].sum = k;
            return ;
        }
        int mid = (l + r) >> 1;
        if(mid >= L) Change(lson, l, mid, L, R, k);
        else Change(rson, mid + 1, r, L, R, k);
        Push_up(i);
    }
    void Sec_Mod(int i, int l, int r, int L, int R, int k) {
        if(tree[i].max < k) return ;
        if(l == r) {
            tree[i].sum = tree[i].max = tree[i].sum % k;
            return ;
        }   
        int mid = (l + r) >> 1;
        if(mid >= L) Sec_Mod(lson, l, mid, L, R, k);
        if(mid < R) Sec_Mod(rson, mid + 1, r, L, R, k);
        Push_up(i);
    }
    int Get_Sum(int i, int l, int r, int L, int R) {
        if(L <= l && r <= R) return tree[i].sum;
        int mid = (l + r) >> 1, ans = 0;
        if(mid >= L) ans += Get_Sum(lson, l, mid, L, R);
        if(mid < R) ans += Get_Sum(rson, mid + 1, r, L, R);
        return ans;
    }
}

signed main()
{
    n = read(), m = read();
    for(int i = 1; i <= n; ++i) a[i] = read();
    Seg::Build(1, 1, n);
    for(int i = 1, opt, l, r, k; i <= m; ++i) {
        opt = read(), l = read(), r = read();
        if(opt == 1) printf("%lld\n", Seg::Get_Sum(1, 1, n, l, r));
        else if(opt == 2) k = read(), Seg::Sec_Mod(1, 1, n, l, r, k);
        else Seg::Change(1, 1, n, l, l, r);
    }
    return 0;
}

CF703D Mishka and Interesting sum

Description

CF703D Mishka and Interesting sum

Solution

• 树状数组

Code

/*
Work by: Suzt_ilymics
Knowledge: 树状数组 
Time: O(能过)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define LL long long
#define orz cout<<"lkp AK IOI!"<<endl

using namespace std;
const int MAXN = 1e6+5;
const int INF = 1e9+7;
const int mod = 1e9+7;

int read(); 
struct Ques{
    int l, r, bh;
    void Read(int x) { l = read(), r = read(), bh = x; }
    bool operator < (const Ques &b) const { return r < b.r; }
}q[MAXN];

int n, m, now_ = 1;
int a[MAXN], date[MAXN], date_num = 0;
int tree[MAXN << 2], sum[MAXN], pre[MAXN], head[MAXN];
int ans[MAXN];

int read(){
    int s = 0, f = 0;
    char ch = getchar();
    while(!isdigit(ch))  f |= (ch == '-'), ch = getchar();
    while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
    return f ? -s : s;
}

int lowbit(int x) { return x & (-x); }
void Add(int x, int val) { for(int i = x; i <= n; i += lowbit(i)) tree[i] ^= val; }
int Query(int x) {
    int res = 0;
    for(int i = x; i; i -= lowbit(i)) res ^= tree[i];
    return res;
}

int main()
{
    n = read();
    for(int i = 1; i <= n; ++i) a[i] = date[i] = read();
    sort(date + 1, date + n + 1), date[0] = -INF;
    for(int i = 1; i <= n; ++i) if(date[i] != date[i - 1]) date[++ date_num] = date[i];
    for(int i = 1; i <= n; ++i) a[i] = lower_bound(date + 1, date + date_num + 1, a[i]) - date;
    for(int i = 1; i <= n; ++i) {
        sum[i] = sum[i - 1] ^ date[a[i]];
        pre[i] = head[a[i]], head[a[i]] = i;
    }
    m = read();
    for(int i = 1; i <= m; ++i) q[i].Read(i);
    sort(q + 1, q + m + 1);
    for(int i = 1; i <= m; ++i) {
        while(now_ <= q[i].r) {
            if(pre[now_]) Add(pre[now_], date[a[now_]]);
            Add(now_, date[a[now_]]);
            ++ now_; 
        }
        ans[q[i].bh] = (Query(q[i].r) ^ Query(q[i].l - 1)) ^ sum[q[i].r] ^ sum[q[i].l - 1];
    }
    for(int i = 1; i <= m; ++i) printf("%d\n", ans[i]);
    return 0;
}

P4211 [LNOI2014]LCA

题目传送

Solution:

嗯……主要在题目转化方面

\(dep[LCA(i,z)]\) 就是 \(i\) 和 \(z\) 到根节点的路径重合的部分。
那么计算 \(i\) 的贡献时可以先用线段树把 \(1 \to i\) 这一段加 \(1\)，然后查询 \(1 \to x\) 这一段区间的值。
每次做的复杂度为 \(O(n \log n \log n)\)
还要做 \(q\) 次

一个很神奇的思路，差分！
考虑离线处理。
区间 \([l,r]\) 可以拆解成 \([1,r] - [1,l-1]\)。把这些左右端点标记下来（这里用的vector储存的）
所以可以从 \(1\) 加到 \(n\)，当遇到一个标记的端点，就立即计算它的贡献。

误区：一开始想成了树上差分，结果把整个题解区翻了一遍都没看懂做法

/*
Work by: Suzt_ilymics
Problem: 不知名屑题
Knowledge: 垃圾算法
Time: O(能过)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<vector>
#define LL long long
#define orz cout<<"lkp AK IOI!"<<endl

using namespace std;
const int MAXN = 1e6+5;
const int INF = 1e9+7;
const int mod = 201314;

struct node { 
    int pre, z;
    bool type;
};

int n, m;
int dep[MAXN], fath[MAXN], top[MAXN], dfn[MAXN], siz[MAXN], son[MAXN], cnt = 0;
int ans[MAXN];
vector <node> a[MAXN];

int read(){
    int s = 0, f = 0;
    char ch = getchar();
    while(!isdigit(ch))  f |= (ch == '-'), ch = getchar();
    while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
    return f ? -s : s;
}

namespace Seg {
    #define lson i << 1
    #define rson i << 1 | 1
    struct Tree{
        int len, lazy, sum;
    }tree[MAXN << 2];
    void Push_up(int i) { tree[i].sum = tree[lson].sum + tree[rson].sum; }
    void Build(int i, int l, int r) {
        tree[i].len = r - l + 1;
        if(l == r) return ;
        int mid = (l + r) >> 1;
        Build(lson, l, mid), Build(rson, mid + 1, r);
        Push_up(i);
    }
    void Push_down(int i) {
        if(tree[i].lazy) {
            tree[lson].lazy += tree[i].lazy;
            tree[rson].lazy += tree[i].lazy;
            tree[lson].sum += tree[lson].len * tree[i].lazy;
            tree[rson].sum += tree[rson].len * tree[i].lazy;
            tree[i].lazy = 0;
        }
    }
    void Add(int i, int l, int r, int L, int R, int val) {
        if(L <= l && r <= R) {
            tree[i].sum += tree[i].len * val;
            tree[i].lazy += val;
            return ;
        }
        Push_down(i);
        int mid = (l + r) >> 1;
        if(mid >= L) Add(lson, l, mid, L, R, val);
        if(mid < R) Add(rson, mid + 1, r, L, R, val);
        Push_up(i);
    }
    int Query(int i, int l, int r, int L, int R) {
//        cout<<l<<" "<<r<<" "<<L<<" "<<R<<"\n";
        if(L <= l && r <= R) return tree[i].sum;
        Push_down(i);
        int mid = (l + r) >> 1, ans = 0;
        if(mid >= L) ans += Query(lson, l, mid, L, R);
        if(mid < R) ans += Query(rson, mid + 1, r, L, R);
        return ans;
    } 
}

namespace Cut {
    struct edge { int to, nxt; }e[MAXN << 1];
    int head[MAXN], num_edge = 1;
    void add_edge(int from, int to) { e[++num_edge] = (edge){to, head[from]}, head[from] = num_edge; }
    void dfs(int u, int fa) {
//        cout<<"dfs1: "<<u<<endl;
        fath[u] = fa, siz[u] = 1, dep[u] = dep[fa] + 1;
        for(int i = head[u]; i; i = e[i].nxt) {
            int v = e[i].to;
            if(v == fa) continue;
            dfs(v, u);
            siz[u] += siz[v];
            if(siz[v] > siz[son[u]]) son[u] = v;
        }
    }
    void dfs2(int u, int tp) {
//        cout<<"dfs2: "<<u<<endl;
        top[u] = tp, dfn[u] = ++cnt;
        if(son[u]) dfs2(son[u], tp);
        for(int i = head[u]; i; i = e[i].nxt) {
            int v = e[i].to;
            if(v == fath[u] || v == son[u]) continue;
            dfs2(v, v);
        }
    }
    void Add(int x, int y) {
        while(top[x] != top[y]) {
            if(dep[top[x]] < dep[top[y]]) swap(x, y);
            Seg::Add(1, 1, n, dfn[top[x]], dfn[x], 1);
            x = fath[top[x]];
        }
        if(dep[x] > dep[y]) swap(x, y);
        Seg::Add(1, 1, n, dfn[x], dfn[y], 1);
    }
    int Query(int x, int y) {
        int ans = 0;
        while(top[x] != top[y]) {
            if(dep[top[x]] < dep[top[y]]) swap(x, y);
            ans += Seg::Query(1, 1, n, dfn[top[x]], dfn[x]);
            x = fath[top[x]];
        }
        if(dep[x] > dep[y]) swap(x, y);
        ans += Seg::Query(1, 1, n, dfn[x], dfn[y]);
        return ans;
    }
}

int main()
{
//    freopen("P4211_1.in","r",stdin);
//    freopen("P4211_1.out","w",stdout);
    n = read(), m = read();
    for(int i = 2, x; i <= n; ++i) x = read() + 1, Cut::add_edge(i, x), Cut::add_edge(x, i);
    Cut::dfs(1, 0), Cut::dfs2(1, 1), Seg::Build(1, 1, n);
    for(int i = 1, l, r, z; i <= m; ++i) {
        l = read() + 1, r = read() + 1, z = read() + 1;
        a[l - 1].push_back((node){i, z, 0});
        a[r].push_back((node){i, z, 1});
    }
    for(int i = 1; i <= n; ++i) {
        Cut::Add(1, i);
        for(int j = 0; j < a[i].size(); ++j) {
            if(a[i][j].type) {
//                cout<<"type1: "<<a[i][j].z<<"\n";
                ans[a[i][j].pre] = (ans[a[i][j].pre] + Cut::Query(1, a[i][j].z)) % mod;
            } else {
//                cout<<"type0: "<<a[i][j].z<<"\n";
                ans[a[i][j].pre] = (ans[a[i][j].pre] - Cut::Query(1, a[i][j].z) + mod) % mod;
            }
        }
    }
    for(int i = 1; i <= m; ++i) printf("%d\n", ans[i]);
    return 0;
}

CF920F SUM and REPLACE

Description

预处理出每个数的约数个数。
线性筛和暴力都能很快的筛出来。
然后修改的时候就暴力修改。
因为对于一个很大的数 \(x\)，它的约数个数至多是 \(\frac{x}{2}\)，所以暴力操作几次就会变成 \(1,2\) 了。复杂度没有问题。

/*
Work by: Suzt_ilymics
Knowledge: ??
Time: O(??)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define int long long
#define LL long long
#define orz cout<<"lkp AK IOI!"<<endl

using namespace std;
const int MAXN = 1e6+5;
const int INF = 1e9+7;
const int mod = 1e9+7;

int n, m;
int a[MAXN], cnt[MAXN];

int read(){
    int s = 0, f = 0;
    char ch = getchar();
    while(!isdigit(ch))  f |= (ch == '-'), ch = getchar();
    while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
    return f ? -s : s;
}

namespace Seg{
    #define lson i << 1
    #define rson i << 1 | 1
    struct Tree{ int lazy, max, sum; }tree[MAXN << 2];
    void Push_up(int i) {
        tree[i].max = max(tree[lson].max, tree[rson].max);
        tree[i].sum = tree[lson].sum + tree[rson].sum;
    }
    void Build(int i, int l, int r) {
        if(l == r) { tree[i].sum = tree[i].max = a[l]; return ; }
        int mid = (l + r) >> 1;
        Build(lson, l, mid), Build(rson, mid + 1, r);
        Push_up(i);
    }   
    void Change(int i, int l, int r, int L, int R) {
        if(tree[i].max <= 2) return ;
        if(l == r) { tree[i].sum = tree[i].max = cnt[tree[i].sum]; return ; }
        int mid = (l + r) >> 1;
        if(mid >= L) Change(lson, l, mid, L, R);
        if(mid < R) Change(rson, mid + 1, r, L, R);
        Push_up(i);
    }
    int Query(int i, int l, int r, int L, int R) {
        if(L <= l && r <= R) return tree[i].sum;
        int mid = (l + r) >> 1, ans = 0;
        if(mid >= L) ans += Query(lson, l, mid, L, R);
        if(mid < R) ans += Query(rson, mid + 1, r, L, R);
        return ans;
    }
}

void Init(int limit) {
    for(int i = 1; i <= limit; ++i) 
        for(int j = i; j <= limit; j += i) 
            ++ cnt[j];
}

signed main()
{
    Init(1000000);
    n = read(), m = read();
    for(int i = 1; i <= n; ++i) a[i] = read();
    Seg::Build(1, 1, n);
    for(int i = 1, opt, l, r; i <= m; ++i) {
        opt = read(), l = read(), r = read();
        if(opt == 1) Seg::Change(1, 1, n, l, r);
        else printf("%lld\n", Seg::Query(1, 1, n, l, r));
    }
    return 0;
}